一次函数

课件23张PPT。2019/3/141§6.2 一次函数2019/3/142一般的，在某个变化过程中，有两个变量x和y，如果给定一个x值，相应的就确定一个y值，那么我们称y是x的函数(fun_ction)，其中x是自变量， y是因变量。1、函数的定义：2、函数的表示法：可以用三种方法
①图象法、
②列表法、
③解析式法（关系式法）2019/3/1433、有关概念：一般地，如果y是x的函数，其中x是自变量，y是因变量时记作y=f(x).其中，自变量的取值范围叫函数的定义域，所对应的因变量的取值范围叫函数的值域。对应法则是函数y对自变量x的依赖关系的具体体现，也是区别各种形式的函数的主要标志。函数的定义域、值域和对应法则称作函数的三要素。大展身手实验一、请同学们测量弹簧的自然长度，再测量在弹性限度内，所挂钩码的个数X每增加一个时弹簧的总长度Y。（注每个钩码的质量相同）
(1)计算所挂钩码的个数为1个，2个和3个时的长度，并填入下表：
（2）你能写出x与Y之间的关系吗？Y是X的函数吗？
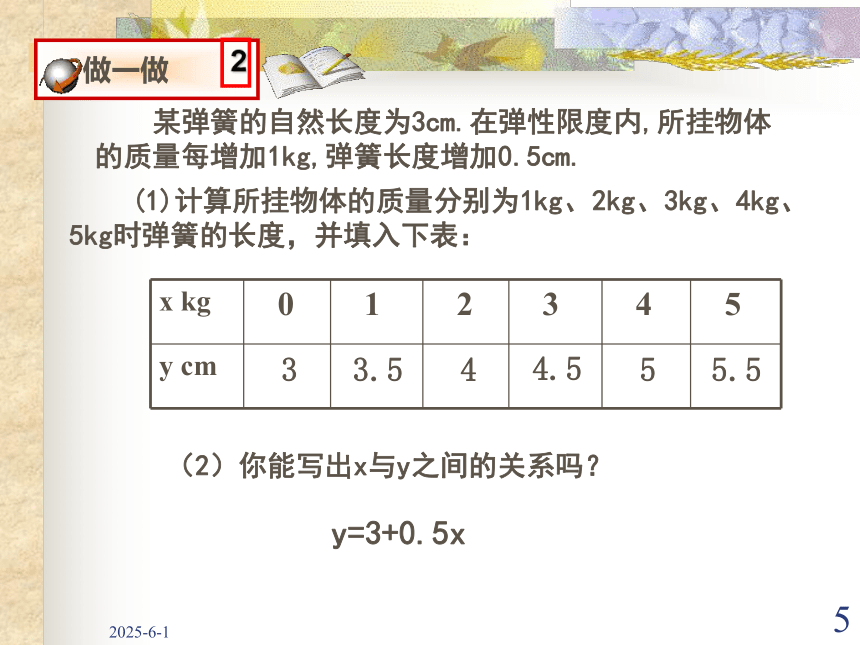
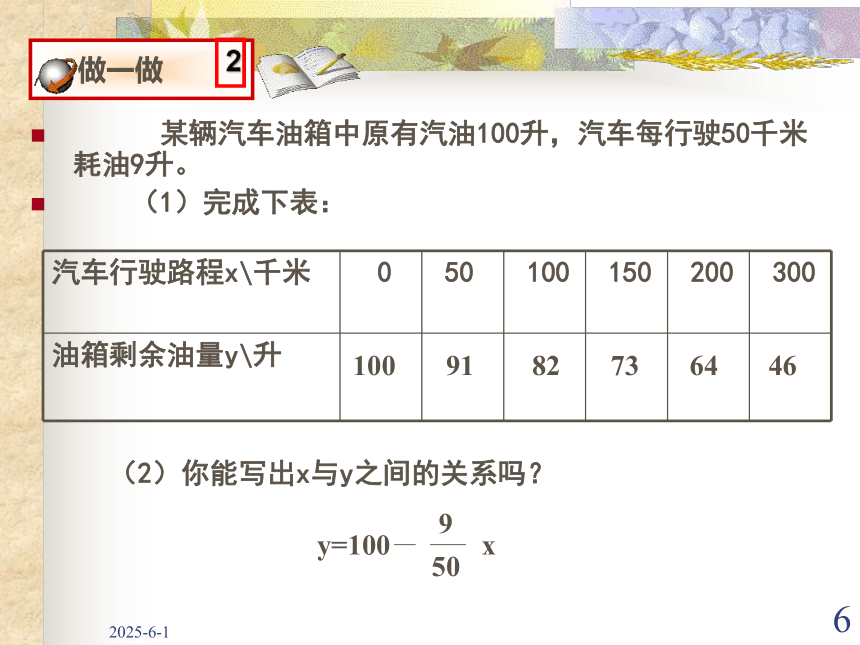
2019/3/145（2）你能写出x与y之间的关系吗？3y=3+0.5x 某弹簧的自然长度为3cm.在弹性限度内,所挂物体的质量每增加1kg,弹簧长度增加0.5cm.3.544.555.5 (1)计算所挂物体的质量分别为1kg、2kg、3kg、4kg、5kg时弹簧的长度，并填入下表：2019/3/146 某辆汽车油箱中原有汽油100升，汽车每行驶50千米耗油9升。
（1）完成下表：
（2）你能写出x与y之间的关系吗？10091824664732019/3/147 上面的两个函数关系式:
y=3+0.5x (1)
y=100－0.18X (2)

大家讨论一下,这两个函数关系式有什么共同特点吗?请小组间交流。
2019/3/148 若两个变量x,y间的关系式可以表示成y=kx+b(k,b为常数,k不为零）的形式,则称y是x的一次函数x为自变量,y为因变量.定义： 特别地,当b=0时,称y是x的正比例函数. y=0.5x+3 (1)
y=－0.18X+100 (2)正比例函数是特殊的一次函数一次函数关系式的左右两边必须是整式！注意：(1)叙述函数定义时，括号内的部分不能遗漏，它是定义的重要组成部分，要明确常数k、b的取值范围．
(2)要熟悉x的一次函数的定义，能由解析式和文字语言结合转换成文字语言的叙述，即函数的解析式是x的一次二项式，其中x的系数k取非零实数，另一项是常数项b，b取任意实数．
另外，应明白正比例函数是一次函数的特例，即所有的正比例函数一定是一次函数，而一次函数y＝kx+b不一定是正比例函数．
2019/3/1410例1：下列函数关系式中，那些是一次函数？哪些是正比例函数?（1）y=-x-4 它是一次函数，但不是正比例函数（2）y=x2它不是一次函数，更不是正比例函数（3）y=2πx它是一次函数，也是正比例函数（4）y=1/x它不是一次函数，更不是正比例函数2019/3/1411下列函数中,哪些是一次函数？
(1) Y = -3X+7
(2) Y = 6X2-3X
(3) Y = 8X
(4) Y = 1+9X 练习12019/3/1412例1:写出下列各题中x与y之间的关系式,并判断:是否为的一次函数？是否为正比函数？ (1)汽车以６０千米时的速度匀速行驶,行驶路程y(千米)与行驶时间x(时)之间的关系; (2)圆的面积y(平方厘米)与它的半径x(厘米)之间的关系; (3)一棵树现在高50厘米,每个月长高2厘米,x月后这棵树的高度为y(厘米). 解：由路程=速度×时间，得y=60x ,y是x的 一次函数,也是x的正比例函数。 解：由圆的面积公式，得y= πx2,y不是x的正比例函数，也不是x的一次函数。 解：这棵树每月长高2厘米，x个月长高了2x厘米，因而y=50+2x，y是x的一次函数，但不是x的正比例函数。2019/3/1413练习：列出下列函数关系式，判别其中哪些为一次函数、正比例函数．
(1)正方形周长p和一边的长a．
(2)圆的面积A与半径R．
(3)长a一定时矩形面积y与宽x．
(4)买15斤梨售价20元．售价y与斤数x．
(5)定期存100元本金，月利率1.8％，本息y与所存月数x．
(6)水库原存水Q立方米，现以每小时a立方米的流量开闸放水，同时上游以每小时b立方米的流量向水库注水，求这时水库的蓄水量M与时间t的函数关系．(1)p=4a．则p为a的一次函数，也是正比例函数．
(2)A=πR2，自变量R的次数是二次，所以不是一次函数，也不是正比例函数．
(3)y=ax，自变量x为一次且系数a为长度(不为零)．则y是x的一次函数，也是x的正比例函数．
(4)是一次函数，也是正比例函数．
(5)y=100+100×1.8%x，自变量x的次数为一次，又含有常数项．则y是x的一次函数但不是正比例函数．
(6)M=Q+(b-a)t，因为自变量t的次数为一次，
当a≠b时，M是t的一次函数．
若Q=0时，M是t的正比例函数；
若a=b时，M是常量函数，不是t的一次函数． 2019/3/14151、二十五中某同学家住白楼下，离校约3000米，骑自行车每分钟行驶300米，
（1）完成下表
（2）你能写出y与x之间的关系式吗？
y =3000-300x 3000270024002100180015000300600900120015002019/3/14162、某弹簧的自然长度为9厘米，在弹簧限度内，
所挂物体的个数x每增加1个，弹簧长度y增加8
厘米，
（1）完成下表：
（2）你能写出y与x之间的关系式吗？y=9+8x91725332019/3/1417 (1)当月收入大于800元而又小于1300元时,写出应缴所得税y(元)与收入x(元)之间的关系式.(2)某人月收入为960元,他应缴所得税多少元?（1160-800）*5%=18元。 例2:我国现行个人工资、薪金所得税征收办法规定：月收入低于800元的部分不收税；月收入超过800元但低于1300元的部分征收5%的个人所得税……如某人月收入1160元,他应缴个人工资、薪金所得税为 解：当月收入大于800元而小于1300元时，
y=0.05×(x-800).解：当x=960时，y=0.05×(960-800)=8（元）2019/3/1418 (1)当月收入大于800元而又小于1300元时,写出应缴所得税y(元)与收入x(元)之间的关系式. (3)如某人本月缴所得税19.2元,那么此人本月工资、薪金是多少元？（1160-800）*5%=18元。 例2:我国现行个人工资、薪金所得税征收办法规定：月收入低于800元的部分不收税；月收入超过800元但低于1300元的部分征收5%的个人所得税……如某人月收入1160元,他应缴个人工资、薪金所得税为 解：当月收入大于800元而小于1300元时，
y=0.05×(x-800). 解：设此人本月工资、薪金是x元，则
19.2=0.05×(x-800), x=1184
即本月工资、薪金是1184元。2019/3/1419100 200 300 4005101520 例2:我国现行个人工资、薪金所得税征收办法规定：月收入低于800元的部分不收税；月收入超过800元但低于1300元的部分征收5%的个人所得税……如某人月收入1160元,他应缴个人工资、薪金所得税为（1160-800）*5%=18元。2019/3/1420100 200 300 4005101520 例2:我国现行个人工资、薪金所得税征收办法规定：月收入低于800元的部分不收税；月收入超过800元但低于1300元的部分征收5%的个人所得税……如某人月收入1160元,他应缴个人工资、薪金所得税为（1160-800）*5%=18元。练习： 要把储水量为2000立方米的水池中的水抽干，现用每小时抽水50立方米的抽水机抽水，写出水池中剩余水量y与抽水时间t(时)之间的函数关系式，并求自变量t的取值范围．
分析：t小时抽水50t立方米，从储水量中减去50t，得剩余水量．
解：y＝2000－50t．
从实际问题的意义知，y≥0，即2000－50t≥0，
解得t≤40；又t≥0，
综上，得自变量t的取值范围是0≤t≤40． 例题： 已知y+p与x-q成正比例(其中p、q是常数)
(1)求证y是x的一次函数．
(2)如果x=-1时，y=-15；x=7时，y=1，求这个一次函数的解析式 2019/3/1423证明： (1)∵y+p与x-q成正比例，
则y+p=k(x-q)(k为非零常数)
整理，得y=kx-(kq+p)
因为k、p、q均为常数，
所以-(kq+P)也是常数，且k≠0
因此y是x的一次函数．
(2)∵y是x的一次函数，设y=kx+b(k≠0)．
将x=-1，y=-15；x=7，y=1代入，得 一次函数的解析式为y=2x-13．