全等三角形的判定(1)--SSS(广东省中山市)
文档属性
| 名称 | 全等三角形的判定(1)--SSS(广东省中山市) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-04 20:06:00 | ||
图片预览


文档简介
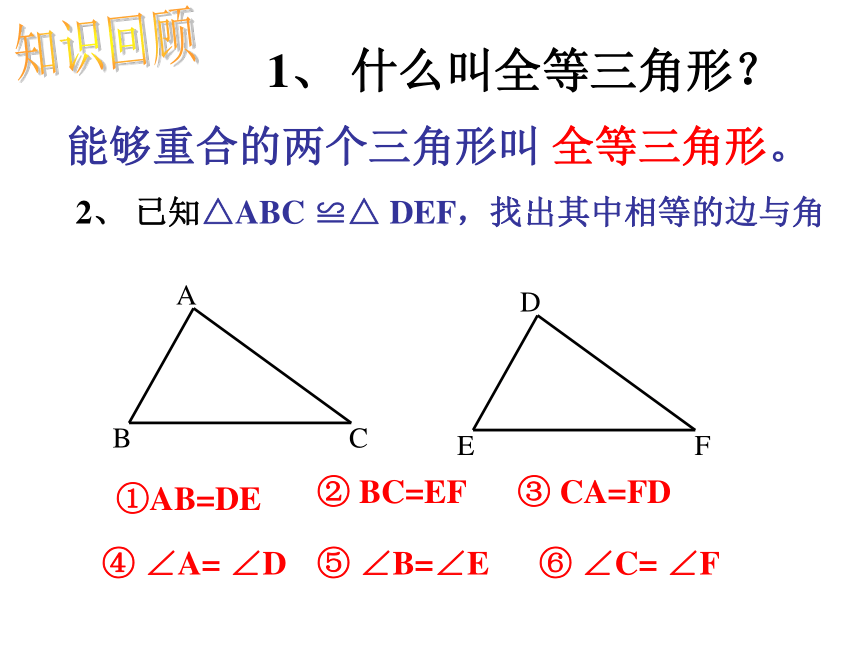
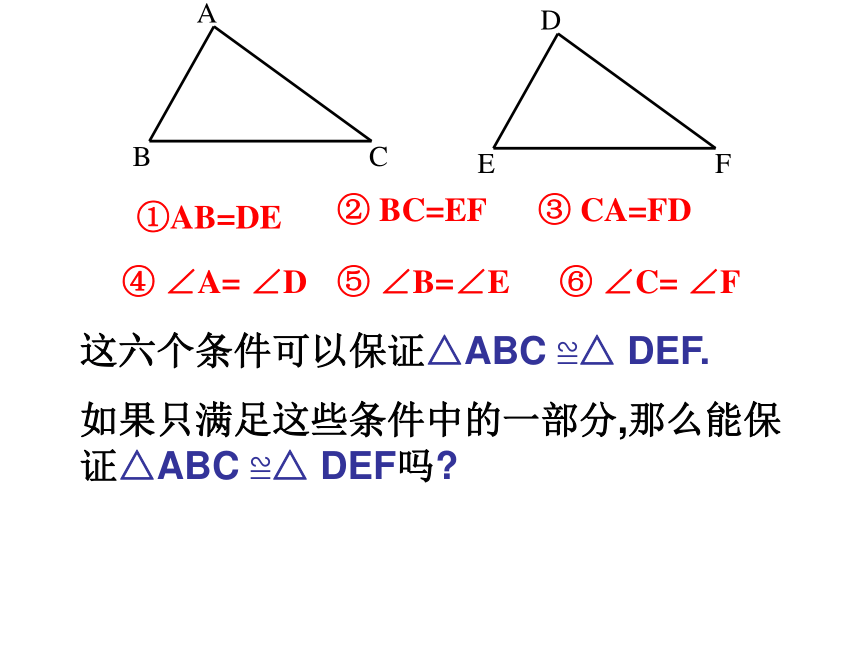
课件18张PPT。§11.2 三角形全等的判定(一)知识回顾 1、 什么叫全等三角形?能够重合的两个三角形叫 全等三角形。 2、 已知△ABC ≌△ DEF,找出其中相等的边与角①AB=DE③ CA=FD② BC=EF④ ∠A= ∠D⑤ ∠B=∠E⑥ ∠C= ∠F①AB=DE③ CA=FD② BC=EF④ ∠A= ∠D⑤ ∠B=∠E⑥ ∠C= ∠F这六个条件可以保证△ABC ≌△ DEF.
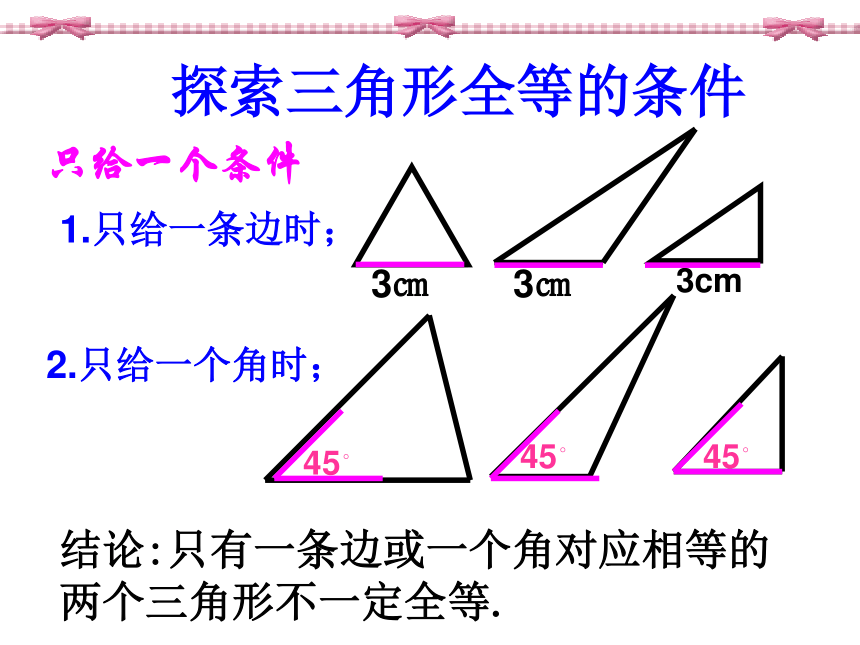
如果只满足这些条件中的一部分,那么能保证△ABC ≌△ DEF吗?2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。 1. 只给一个条件(一组对应边或一组对应角)画出的三角形一定全等吗? (2)三角形的一条边4cm,一个内角为30°。(3)三角形的两个内角分别为30°和50°.(1)三角形的两条边分别为4cm、6cm.探索三角形全等的条件1.只给一条边时;3㎝3㎝只给一个条件45?45?2.只给一个角时;3cm45?结论:只有一条边或一个角对应相等的两个三角形不一定全等.如果给出两个条件画三角形,
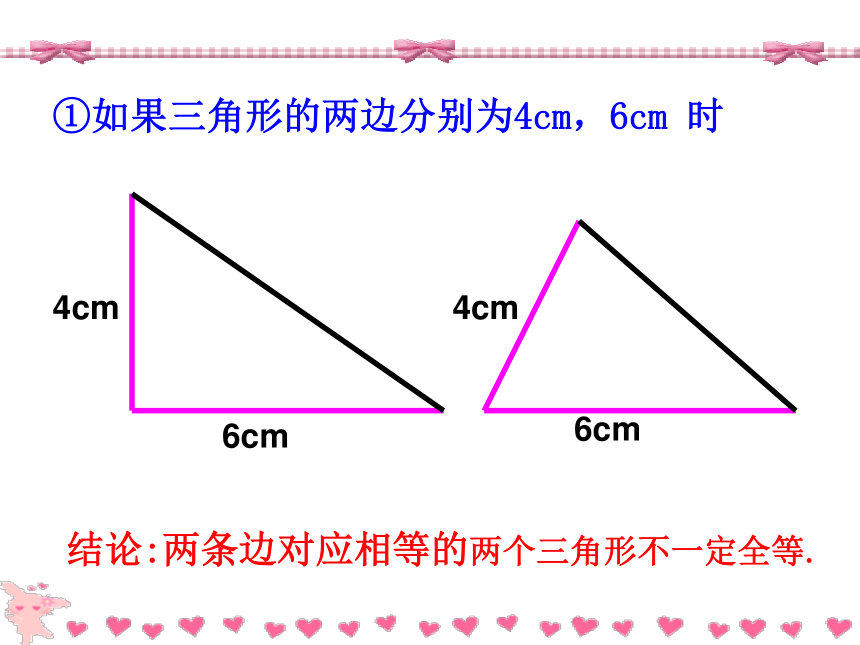
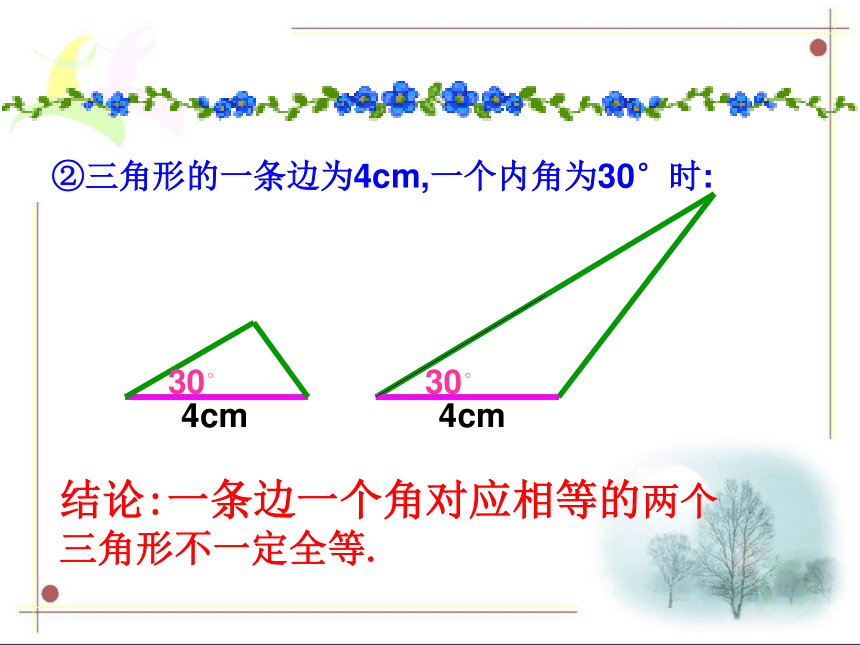
你能说出有哪几种可能的情况?①两边;③两角。②一边一角;①如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm结论:两条边对应相等的两个三角形不一定全等.②三角形的一条边为4cm,一个内角为30°时:4cm4cm30?30?结论:一条边一个角对应相等的两个三角形不一定全等.③如果三角形的两个内角分别是30°,45°时结论:两个角对应相等的两个三角形不一定全等.根据三角形的内角和为180度,则第三角一定确定,所以当三内角对应相等时,两个三角形不一定全等两个条件
①两角;
②两边;
③一边一角。结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。一个条件
①一角;
②一边;你能得到什么结论吗?如果给出三个条件画三角形,
你能说出有哪几种可能的情况?①三角;②三边;③两边一角;④两角一边。2、画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?画法: 1.画线段AB=3㎝;2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两弧交于点C;3. 连接线段AC、BC.结论:三边对应相等的两个三角形全等.可简写为边边边或SSS思考:你能用三角形的稳定性来说明SSS公理吗?如何用符号语言来表达呢?在△ABC与△DEF中ABCDEFAB=DE
AC=DF
BC=EF∴△ABC≌△DEF(SSS)判断两个三角形全等的推理过程,叫做证明三角形全等。 A C B D 分析:要证明两个三角形全等,需要那些条件?证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)例1 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD若要求证:∠B=∠C,你会吗?练习: 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADCABCDACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC(SSS)证明:在△ABC和△ADC中=已知已知 公共边小结:1.这节课学习了什么内容?2.要判定两个三角形全等至少需要多少个条件?3.今天我们学习了判定三角形全等的哪些方法?作业:1.已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADC2.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 3.如图,C是AB的中点,AD=CE,CD=BE,△ACD和△CBE是否全等?试说明理由。 再见
如果只满足这些条件中的一部分,那么能保证△ABC ≌△ DEF吗?2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。 1. 只给一个条件(一组对应边或一组对应角)画出的三角形一定全等吗? (2)三角形的一条边4cm,一个内角为30°。(3)三角形的两个内角分别为30°和50°.(1)三角形的两条边分别为4cm、6cm.探索三角形全等的条件1.只给一条边时;3㎝3㎝只给一个条件45?45?2.只给一个角时;3cm45?结论:只有一条边或一个角对应相等的两个三角形不一定全等.如果给出两个条件画三角形,
你能说出有哪几种可能的情况?①两边;③两角。②一边一角;①如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm结论:两条边对应相等的两个三角形不一定全等.②三角形的一条边为4cm,一个内角为30°时:4cm4cm30?30?结论:一条边一个角对应相等的两个三角形不一定全等.③如果三角形的两个内角分别是30°,45°时结论:两个角对应相等的两个三角形不一定全等.根据三角形的内角和为180度,则第三角一定确定,所以当三内角对应相等时,两个三角形不一定全等两个条件
①两角;
②两边;
③一边一角。结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。一个条件
①一角;
②一边;你能得到什么结论吗?如果给出三个条件画三角形,
你能说出有哪几种可能的情况?①三角;②三边;③两边一角;④两角一边。2、画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?画法: 1.画线段AB=3㎝;2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两弧交于点C;3. 连接线段AC、BC.结论:三边对应相等的两个三角形全等.可简写为边边边或SSS思考:你能用三角形的稳定性来说明SSS公理吗?如何用符号语言来表达呢?在△ABC与△DEF中ABCDEFAB=DE
AC=DF
BC=EF∴△ABC≌△DEF(SSS)判断两个三角形全等的推理过程,叫做证明三角形全等。 A C B D 分析:要证明两个三角形全等,需要那些条件?证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)例1 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD若要求证:∠B=∠C,你会吗?练习: 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADCABCDACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC(SSS)证明:在△ABC和△ADC中=已知已知 公共边小结:1.这节课学习了什么内容?2.要判定两个三角形全等至少需要多少个条件?3.今天我们学习了判定三角形全等的哪些方法?作业:1.已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADC2.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 3.如图,C是AB的中点,AD=CE,CD=BE,△ACD和△CBE是否全等?试说明理由。 再见
