7.2.2用坐标表示平移 教案
文档属性
| 名称 | 7.2.2用坐标表示平移 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-24 11:35:32 | ||
图片预览

文档简介
7.2.2 用坐标表示平移教案
广西崇左市龙州县第一中学 周伟兵
学校 主备人 时间
设计理 念 在学生学习了位置平移的概念和性质的基 ( http: / / www.21cnjy.com )础上进行的,主要是引导学生运用分类思想,依次经过点或图形平移的观察、画图、比较、推理、归纳等活动,最终探索出点的坐标变化与点平移的关系,图形各个点的坐标变化与图形平移的关系,体验坐标这种数的形式与平移这种图形的形式之间的相互联系.
教学目标 知识与技能:1.了解坐标平面内,平移点的坐标变化;会写出平移变化后,点的坐标.2.由点的坐标变化,能判断点的平移情况.过程与方法: 在坐标系中,通过对点坐标的平移变化的探究,掌握数性结合的思想方法.情感态度与价值观: 在坐标系中,通过对点坐标的平移变化的探究,培养学生合作交流的意识和探索精神.
重点 点坐标平移的变化规律.
难点 通过平移确定点坐标的变化.
方法 实验、探究式教学法 课 型 新授课
教 学 过 程
教学环节 教 学 内 容 师 生 活 动 设计意图
3.(课件)已知三角形ABC,平移三角形ABC使点A和点A’重合。
4.把鱼往左平移6cm。(假设每小格是1cm) 学生回顾,师生补充. 导入新课
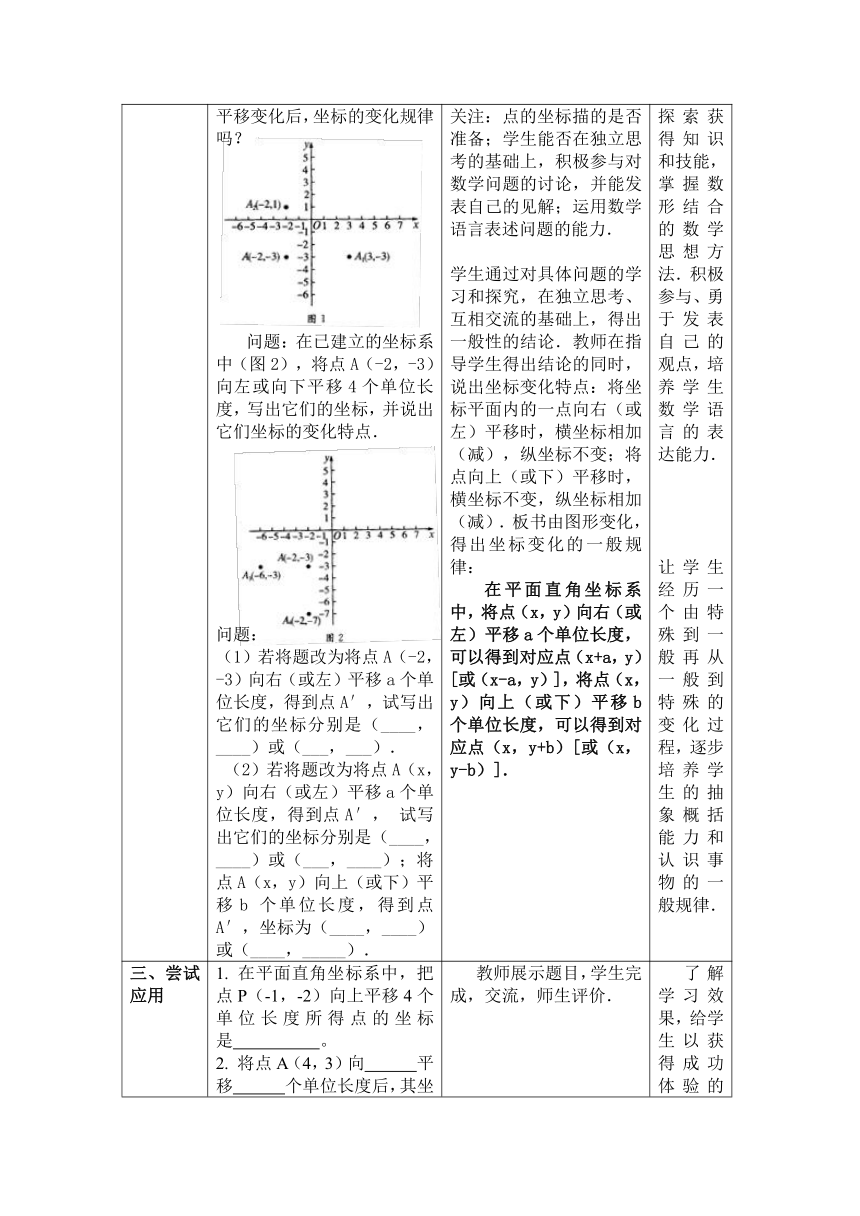
二、自主探究1 问题:(1)请同学们准备好 ( http: / / www.21cnjy.com )坐标纸,并在坐标 ( http: / / www.21cnjy.com )纸上建立坐标系,描出点A(-2,-3).将点A向右平移5个单位长度,得到点A1,在图1上标出这个点,并写出它的坐标;将点A(-2,-3)向上平移4个单位长度,得到点A2,在图1上标出这个点,并写出它的坐标;你能说出上述两种平移变化后,坐标的变化规律吗?问题:在已建立的坐标系中(图2),将点A(-2,-3)向左或向下平移4个单位长度,写出它们的坐标,并说出它们坐标的变化特点.问题:(1)若将题改为将点A(-2,-3)向右( ( http: / / www.21cnjy.com )或左)平移a个单位长度,得到点A′,试写出它们的坐标分别是(____,____)或(___,___). (2)若将题改为将点A(x,y)向右(或左)平移a个单位长度,得到点A′,试写出它们的坐标分别是(____,____)或(___,____);将点A(x,y)向上(或下)平移b个单位长度,得到点A′,坐标为(____,____)或(____,_____). 教师在学生回答的基础上,进一步 ( http: / / www.21cnjy.com )补充、完善,得出结论.将点A(-2,-3)向右平移5个单位长度,得到的新坐标是:纵坐标不变,横坐标加5.如将A(-2,-3)向上平移4个单位长度是:横坐标不变,纵坐标加4.[答案:A1(3,-3),A2(-2,1)]在活动中教师应重点关注:点的坐标描 ( http: / / www.21cnjy.com )的是否准备;学生能否在独立思考的基础上,积极参与对数学问题的讨论,并能发表自己的见解;运用数学语言表述问题的能力.学生通过对具体问题的学习和探究,在 ( http: / / www.21cnjy.com )独立思考、互相交流的基础上,得出一般性的结论.教师在指导学生得出结论的同时,说出坐标变化特点:将坐标平面内的一点向右(或左)平移时,横坐标相加(减),纵坐标不变;将点向上(或下)平移时,横坐标不变,纵坐标相加(减).板书由图形变化,得出坐标变化的一般规律: 在平面直角坐标系中,将点(x,y)向 ( http: / / www.21cnjy.com )右(或左)平移a个单位长度,可以得到对应点(x+a,y)[或(x-a,y)],将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)[或(x,y-b)]. 通过学生亲自动手实 ( http: / / www.21cnjy.com )践,独立思考,相互交流,在“做数学”的活动中,通过自主探索获得知识和技能,掌握数形结合的数学思想方法.积极参与、勇于发表自己的观点,培养学生数学语言的表达能力.让学生经历一个由特殊到一般再从一般到特殊的变化过程,逐步培养学生的抽象概括能力和认识事物的一般规律.
1. 在平面直角坐标系中 ( http: / / www.21cnjy.com ),把点P(-1,-2)向上平移4个单位长度所得点的坐标是 。
2. 将点A(4,3)向 平移 个单位长度后,其坐标的变化是( 6, 3 ) 。
3. 已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,则A′的坐标为_______.
4.在平面直角坐标系中,有一点P(-2,4),若将点P:(1)向左平移2个单位长度,所得点的坐标为_________; (2)向右平移3个单位长度,所得点的坐标为_________ ;(3)向下平移4个单位长度,所得点的坐标为_________ ;(4)向上平移5个单位长度,所得点的坐标为_________ ; 教师展示题目,学生完成,交流,师生评价. 了解学习效果,给学生以获得成功体验的机会,激发他们学习的兴趣和积极性.
四、巩固提高 在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线。 学生首先独立思考,然后小组交流, ( http: / / www.21cnjy.com )全班评价。教师参与小组讨论,认真倾听学生发言,及时掌控学生对知识的掌握程度。在活动中教师应重点关注:(1)学生对图形平移后,点坐标的变化规律的进一步认识;(2)学生应用知识解决问题的能力. 巩固所学知识,为图形在坐标系中的平移做铺垫.
(1)如图, △ ABC三个顶点的坐标 ( http: / / www.21cnjy.com )
A(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个顶点的
横坐标都减去6,纵坐标不变
依次连接A1,B1,C1,各
点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的大小、 形状和位置上有什么关系?
在活动中教师应重点关注:点的坐标描 ( http: / / www.21cnjy.com )的是否准备;学生能否在独立思考的基础上,积极参与对数学问题的讨论,并能发表自己的见解;运用数学语言表述问题的能力.学生通过对具体问题的学习和探究,在独立思考、互相交流的基础上,得出一般性的结论.教师在指导学生得出结论的同时,说出坐标变化特点).板书由图形变化,得出坐标变化的一般规律:图形上点的坐标变化与图形平移间的关系1)横坐标变化,纵坐标不变:原图形上的点(x,y),(x+a,y)向右平移a个单位,原图形上的点(x,y) (x-a,y) 左平移a个单位(2)横坐标不变,纵坐标变化原图形上的点(x,y) (x,y+b) 上平移b个单位原图形上的点(x,y) ,(x,y-b) 下平移b个单位
1.线段CD是由线段AB平移得到的。
练习3、
如图,将平行四边形ABC ( http: / / www.21cnjy.com )
ABCD向左平移2单位
长度,再向上移3个
单位长度得到平行四边
形A’B’C’D’,画出平移后的图形,并指出其各
4、图中直角三角形的顶点坐标分别了什么变化?
(2)(3)中的三角形发生了哪些变化
七、体验收获 本节课我们主要学习以下主要内容:1.掌握平移后,点的坐标的变化规律;2.提高学生应用数学知识解决问题的能力. 学生归纳总结,教师补充升华. 培养学生概括的能力,使知识形成体系.
广西崇左市龙州县第一中学 周伟兵
学校 主备人 时间
设计理 念 在学生学习了位置平移的概念和性质的基 ( http: / / www.21cnjy.com )础上进行的,主要是引导学生运用分类思想,依次经过点或图形平移的观察、画图、比较、推理、归纳等活动,最终探索出点的坐标变化与点平移的关系,图形各个点的坐标变化与图形平移的关系,体验坐标这种数的形式与平移这种图形的形式之间的相互联系.
教学目标 知识与技能:1.了解坐标平面内,平移点的坐标变化;会写出平移变化后,点的坐标.2.由点的坐标变化,能判断点的平移情况.过程与方法: 在坐标系中,通过对点坐标的平移变化的探究,掌握数性结合的思想方法.情感态度与价值观: 在坐标系中,通过对点坐标的平移变化的探究,培养学生合作交流的意识和探索精神.
重点 点坐标平移的变化规律.
难点 通过平移确定点坐标的变化.
方法 实验、探究式教学法 课 型 新授课
教 学 过 程
教学环节 教 学 内 容 师 生 活 动 设计意图
3.(课件)已知三角形ABC,平移三角形ABC使点A和点A’重合。
4.把鱼往左平移6cm。(假设每小格是1cm) 学生回顾,师生补充. 导入新课
二、自主探究1 问题:(1)请同学们准备好 ( http: / / www.21cnjy.com )坐标纸,并在坐标 ( http: / / www.21cnjy.com )纸上建立坐标系,描出点A(-2,-3).将点A向右平移5个单位长度,得到点A1,在图1上标出这个点,并写出它的坐标;将点A(-2,-3)向上平移4个单位长度,得到点A2,在图1上标出这个点,并写出它的坐标;你能说出上述两种平移变化后,坐标的变化规律吗?问题:在已建立的坐标系中(图2),将点A(-2,-3)向左或向下平移4个单位长度,写出它们的坐标,并说出它们坐标的变化特点.问题:(1)若将题改为将点A(-2,-3)向右( ( http: / / www.21cnjy.com )或左)平移a个单位长度,得到点A′,试写出它们的坐标分别是(____,____)或(___,___). (2)若将题改为将点A(x,y)向右(或左)平移a个单位长度,得到点A′,试写出它们的坐标分别是(____,____)或(___,____);将点A(x,y)向上(或下)平移b个单位长度,得到点A′,坐标为(____,____)或(____,_____). 教师在学生回答的基础上,进一步 ( http: / / www.21cnjy.com )补充、完善,得出结论.将点A(-2,-3)向右平移5个单位长度,得到的新坐标是:纵坐标不变,横坐标加5.如将A(-2,-3)向上平移4个单位长度是:横坐标不变,纵坐标加4.[答案:A1(3,-3),A2(-2,1)]在活动中教师应重点关注:点的坐标描 ( http: / / www.21cnjy.com )的是否准备;学生能否在独立思考的基础上,积极参与对数学问题的讨论,并能发表自己的见解;运用数学语言表述问题的能力.学生通过对具体问题的学习和探究,在 ( http: / / www.21cnjy.com )独立思考、互相交流的基础上,得出一般性的结论.教师在指导学生得出结论的同时,说出坐标变化特点:将坐标平面内的一点向右(或左)平移时,横坐标相加(减),纵坐标不变;将点向上(或下)平移时,横坐标不变,纵坐标相加(减).板书由图形变化,得出坐标变化的一般规律: 在平面直角坐标系中,将点(x,y)向 ( http: / / www.21cnjy.com )右(或左)平移a个单位长度,可以得到对应点(x+a,y)[或(x-a,y)],将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)[或(x,y-b)]. 通过学生亲自动手实 ( http: / / www.21cnjy.com )践,独立思考,相互交流,在“做数学”的活动中,通过自主探索获得知识和技能,掌握数形结合的数学思想方法.积极参与、勇于发表自己的观点,培养学生数学语言的表达能力.让学生经历一个由特殊到一般再从一般到特殊的变化过程,逐步培养学生的抽象概括能力和认识事物的一般规律.
1. 在平面直角坐标系中 ( http: / / www.21cnjy.com ),把点P(-1,-2)向上平移4个单位长度所得点的坐标是 。
2. 将点A(4,3)向 平移 个单位长度后,其坐标的变化是( 6, 3 ) 。
3. 已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,则A′的坐标为_______.
4.在平面直角坐标系中,有一点P(-2,4),若将点P:(1)向左平移2个单位长度,所得点的坐标为_________; (2)向右平移3个单位长度,所得点的坐标为_________ ;(3)向下平移4个单位长度,所得点的坐标为_________ ;(4)向上平移5个单位长度,所得点的坐标为_________ ; 教师展示题目,学生完成,交流,师生评价. 了解学习效果,给学生以获得成功体验的机会,激发他们学习的兴趣和积极性.
四、巩固提高 在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线。 学生首先独立思考,然后小组交流, ( http: / / www.21cnjy.com )全班评价。教师参与小组讨论,认真倾听学生发言,及时掌控学生对知识的掌握程度。在活动中教师应重点关注:(1)学生对图形平移后,点坐标的变化规律的进一步认识;(2)学生应用知识解决问题的能力. 巩固所学知识,为图形在坐标系中的平移做铺垫.
(1)如图, △ ABC三个顶点的坐标 ( http: / / www.21cnjy.com )
A(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个顶点的
横坐标都减去6,纵坐标不变
依次连接A1,B1,C1,各
点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的大小、 形状和位置上有什么关系?
在活动中教师应重点关注:点的坐标描 ( http: / / www.21cnjy.com )的是否准备;学生能否在独立思考的基础上,积极参与对数学问题的讨论,并能发表自己的见解;运用数学语言表述问题的能力.学生通过对具体问题的学习和探究,在独立思考、互相交流的基础上,得出一般性的结论.教师在指导学生得出结论的同时,说出坐标变化特点).板书由图形变化,得出坐标变化的一般规律:图形上点的坐标变化与图形平移间的关系1)横坐标变化,纵坐标不变:原图形上的点(x,y),(x+a,y)向右平移a个单位,原图形上的点(x,y) (x-a,y) 左平移a个单位(2)横坐标不变,纵坐标变化原图形上的点(x,y) (x,y+b) 上平移b个单位原图形上的点(x,y) ,(x,y-b) 下平移b个单位
1.线段CD是由线段AB平移得到的。
练习3、
如图,将平行四边形ABC ( http: / / www.21cnjy.com )
ABCD向左平移2单位
长度,再向上移3个
单位长度得到平行四边
形A’B’C’D’,画出平移后的图形,并指出其各
4、图中直角三角形的顶点坐标分别了什么变化?
(2)(3)中的三角形发生了哪些变化
七、体验收获 本节课我们主要学习以下主要内容:1.掌握平移后,点的坐标的变化规律;2.提高学生应用数学知识解决问题的能力. 学生归纳总结,教师补充升华. 培养学生概括的能力,使知识形成体系.
