山东省青岛市四区联考2023-2024学年高三上学期期中数学试卷(含解析)
文档属性
| 名称 | 山东省青岛市四区联考2023-2024学年高三上学期期中数学试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 858.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 17:27:02 | ||
图片预览




文档简介
2023-2024学年山东省青岛市四区联考高三(上)期中数学试卷
一、单项选择题:本题共8小题,每小题5分,共40分.在年小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)设集合M={2,4,6,8,10},N={x|y=ln(6﹣x)}( )
A.{2,4,6,8,10} B.{2,4,6,8}
C.{2,4,6} D.{2,4}
2.(5分)已知平面向量,且,则t=( )
A. B. C.6 D.﹣6
3.(5分)已知,则tan2θ=( )
A. B. C. D.
4.(5分)若正实数a,b满足a+b=2,则( )
A.有最大值 B.ab有最小值
C.有最大值 D.a2+b2有最大值
5.(5分)已知平行四边形ABCD满足,则=( )
A.1 B.2 C.3 D.4
6.(5分)高为h的密闭圆锥容器中有一部分水,当该容器底面放在水平面上时水面高度为h1,当该容器顶点在水平面上且底面与水平面平行时,水面高度为h2,若h1+h2=h,则h:h2=( )
A. B. C. D.2
7.(5分)已知命题“,使得”为假命题( )
A. B. C. D.
8.(5分)已知,则( )
A.a>b>c B.c>b>a C.a>c>b D.b>c>a
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
(多选)9.(5分)设函数f(x)=ln(cos2x),则( )
A.f(x)为奇函数
B.f(x)的最小正周期为π
C.f(x)存在零点
D.f(x)存在极值点
(多选)10.(5分)正方体ABCD﹣A1B1C1D1中,E,F分别为A1B,B1C的中点,则( )
A.直线EF∥平面ABCD
B.EF⊥AC
C.异面直线EF与直线D1C所成角的大小为60°
D.平面B1CD1到平面BA1D的距离等于EF
(多选)11.(5分)设函数f(x)=sinx﹣cosx,则( )
A.f(x)的图象关于对称
B.函数y=f2(x)的最小正周期为π
C.将曲线y=f(x)上各点横坐标变为原来的2倍,再将曲线向左平移个单位,得到函数的图象
D.函数的最大值为
(多选)12.(5分)已知平面向量满足.则( )
A.
B.
C.
D.向量,则x2+y2+z2的最小值为
三、填空题:本题共4个小题,每小题5分,共20分.
13.(5分)曲线f(x)=e2﹣x过原点的切线方程为 .
14.(5分)已知函数f(x)是定义域为R的奇函数,f(x)+f(2﹣x),则f(3)= .
15.(5分)已知函数,若f(x)=m存在四个不相等的实根x1,x2,x3,x4(x1<x2<x3<x4),则的最小值是 .
16.(5分)在△ABC中,AB=2,将△ABC各边中点连线并折成四面体 ;该四面体的体积为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明,证明过程或演算步骤.
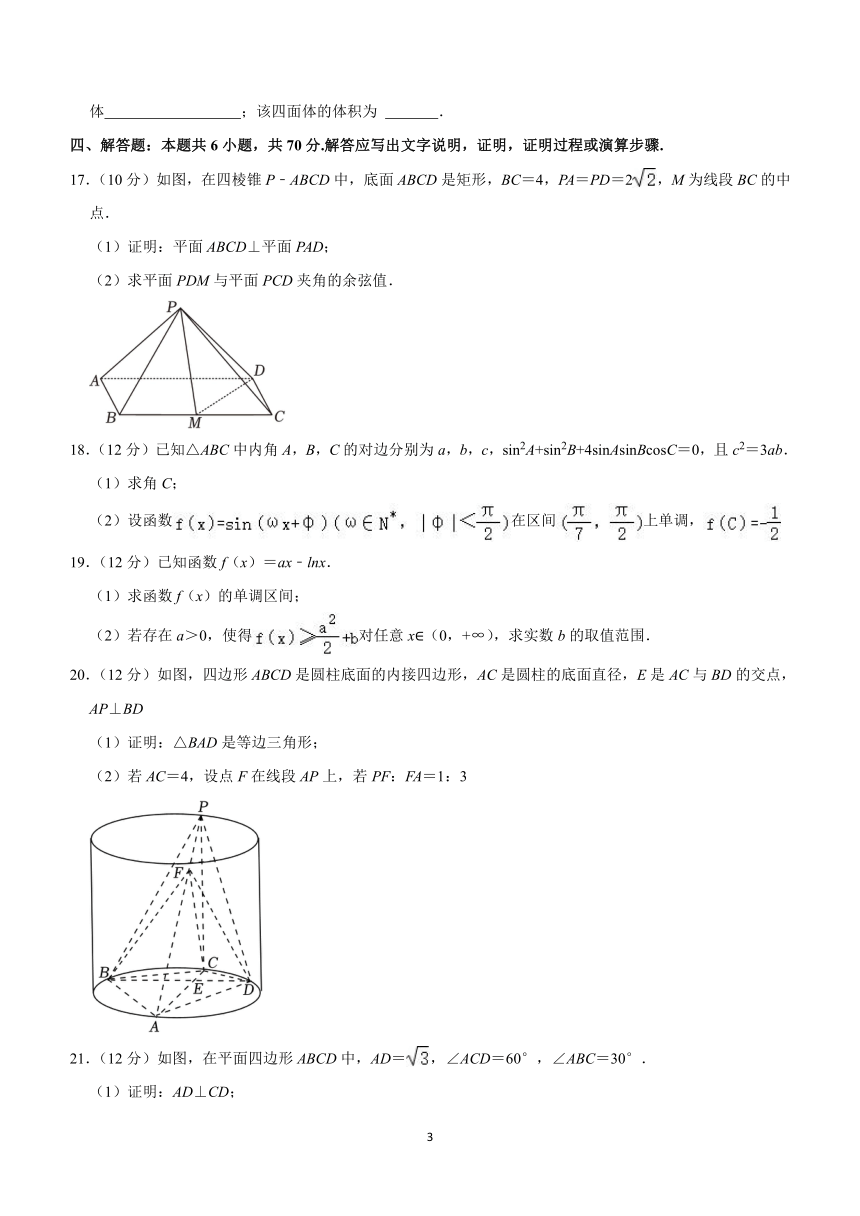
17.(10分)如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,BC=4,PA=PD=2,M为线段BC的中点.
(1)证明:平面ABCD⊥平面PAD;
(2)求平面PDM与平面PCD夹角的余弦值.
18.(12分)已知△ABC中内角A,B,C的对边分别为a,b,c,sin2A+sin2B+4sinAsinBcosC=0,且c2=3ab.
(1)求角C;
(2)设函数在区间上单调,
19.(12分)已知函数f(x)=ax﹣lnx.
(1)求函数f(x)的单调区间;
(2)若存在a>0,使得对任意x∈(0,+∞),求实数b的取值范围.
20.(12分)如图,四边形ABCD是圆柱底面的内接四边形,AC是圆柱的底面直径,E是AC与BD的交点,AP⊥BD
(1)证明:△BAD是等边三角形;
(2)若AC=4,设点F在线段AP上,若PF:FA=1:3
21.(12分)如图,在平面四边形ABCD中,AD=,∠ACD=60°,∠ABC=30°.
(1)证明:AD⊥CD;
(2)求△ABC面积的最大值;
(3)设E为线段AB的中点,求DE的最大值.
22.(12分)已知函数f(x)=ex﹣ax2﹣x.
(1)若函数f(x)在(﹣∞,+∞)上单调递增,求a的值;
(2)当a>时,证明:函数f(x)有两个极值点x1,x2(x1<x2),且f(x2)<1+.
2023-2024学年山东省青岛市四区联考高三(上)期中数学试卷
参考答案与试题解析
一、单项选择题:本题共8小题,每小题5分,共40分.在年小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)设集合M={2,4,6,8,10},N={x|y=ln(6﹣x)}( )
A.{2,4,6,8,10} B.{2,4,6,8}
C.{2,4,6} D.{2,4}
【分析】首先根据对数函数的定义域求集合N,再利用交集的概念求答案.
【解答】解:根据对数函数的定义域得N={x|y=ln(6﹣x)}={x|x<6},
又因为M={6,4,6,2,10},4}.
故选:D.
【点评】本题考查集合的运算,属于基础题.
2.(5分)已知平面向量,且,则t=( )
A. B. C.6 D.﹣6
【分析】根据已知条件,结合向量垂直的性质,即可求解.
【解答】解:,,
,
则4t+6(t+8)=0,解得t=﹣.
故选:A.
【点评】本题主要考查平面向量垂直的性质,属于基础题.
3.(5分)已知,则tan2θ=( )
A. B. C. D.
【分析】根据已知条件,结合三角函数的同角公式,以及正切函数的二倍角公式,即可求解.
【解答】解:,
则sinθ=,
故tanθ=,
所以tan2θ===.
故选:A.
【点评】本题主要考查二倍角的三角函数,属于基础题.
4.(5分)若正实数a,b满足a+b=2,则( )
A.有最大值 B.ab有最小值
C.有最大值 D.a2+b2有最大值
【分析】根据已知条件,结合基本不等式的公式,依次求解.
【解答】解:a+b=2,
则=,当且仅当a=b=1时的,
故有最小值;
,当且仅当a=b=1时,
故ab有最大值1,
=4,当且仅当a=b=7时,
故有最大值2;
a2+b5=(a+b)2﹣2ab=7﹣2ab≥4﹣8 =5,等号成立,
故a2+b2有最小值2,故D错误.
故选:C.
【点评】本题主要考查基本不等式的公式,属于基础题.
5.(5分)已知平行四边形ABCD满足,则=( )
A.1 B.2 C.3 D.4
【分析】结合平面向量的线性运算,以及数量积运算,即可求解.
【解答】解:,
则+,
由平行四边形的性质可知,,
,
故,解得.
故选:B.
【点评】本题主要考查平面向量的数量积运算,属于基础题.
6.(5分)高为h的密闭圆锥容器中有一部分水,当该容器底面放在水平面上时水面高度为h1,当该容器顶点在水平面上且底面与水平面平行时,水面高度为h2,若h1+h2=h,则h:h2=( )
A. B. C. D.2
【分析】结合圆锥的体积公式求解.
【解答】解:由题意可得|PO|=h,|OO1|=h1,|PO6|=h2,
又h1+h4=h,
即V小圆锥:V大圆锥=1:2,
又△PCO8~△PAO,
则,
则==,
则,
则.
故选:C.
【点评】本题考查了圆锥的体积公式,属基础题.
7.(5分)已知命题“,使得”为假命题( )
A. B. C. D.
【分析】由题意开始命题的否定为真命题,求出+的最小值即可,设t=sinθ+cosθ,由θ的范围可得t的范围,及sinθ cosθ的范围,进而可得+的最小值,即求出a的范围.
【解答】解:由题意可得 θ∈(0,),使得a≤+,只需要a≤(+)min即可,
而+=,
设t=sinθ+cosθ=sin(θ+),),所以θ+,),所以sin(θ+,1],
即t∈(1,],且sinθcosθ=,
所以+==,
令y=t﹣,则y'=7+,所以函数y在t∈(4,,所以ymax=﹣=,
所以+的最小值为,
所以a≤2,即a的范围(﹣∞,5].
故选:A.
【点评】本题考查三角函数的性质的应用,属于基础题.
8.(5分)已知,则( )
A.a>b>c B.c>b>a C.a>c>b D.b>c>a
【分析】利用作商法比较c与b,利用作差法比较a与b,综合可得结论.
【解答】解:=4,,
因为当 时,
所以,
所以c>b,
b﹣a====,
因为,所以,
所以b﹣a>0,b>a,
综上,c>b>a.
故选:B.
【点评】本题主要考查函数值大小的比较,考查逻辑推理能力,属于中档题.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
(多选)9.(5分)设函数f(x)=ln(cos2x),则( )
A.f(x)为奇函数
B.f(x)的最小正周期为π
C.f(x)存在零点
D.f(x)存在极值点
【分析】利用三角函数的性质以及对数型复合函数的单调性,结合函数的周期性,零点、极值点的概念求解.
【解答】解:A.由cos2x>0,
解得,
所以函数f(x)=ln(cos2x)的定义域为,
且f(﹣x)=ln[cos(﹣2x)]=ln(cos2x)=f(x).
所以函数f(x)为偶函数,故A错误;
B.因为函数y=cos(3x)的最小正周期为π,故B正确;
C.令f(x)=ln(cos2x)=0,所以2x=2kπ,
即x=kπ,k∈Z为函数f(x)的零点;
D.因为函数y=cos(2x)在,单调递减,
所以函数f(x)=ln(cos2x)在单调递增,,
所以x=kπ,k∈Z为函数f(x)=ln(cos2x)的极大值点.
故选:BCD.
【点评】本题考查了函数的奇偶性、单调性和周期性,函数的零点与方程根的关系和函数的极值点,考查了转化思想,属中档题.
(多选)10.(5分)正方体ABCD﹣A1B1C1D1中,E,F分别为A1B,B1C的中点,则( )
A.直线EF∥平面ABCD
B.EF⊥AC
C.异面直线EF与直线D1C所成角的大小为60°
D.平面B1CD1到平面BA1D的距离等于EF
【分析】A选项,建立空间直角坐标系,求出平面ABCD的法向量为,从而得到,EF∥平面ABCD;B选项,,B错误;C选项,利用空间向量异面直线夹角余弦公式求出答案;D选项,先求出两个平面的法向量,得到两平面平行,进而由点到平面距离公式求出答案.
【解答】解:A选项,以A为坐标原点,AD1所在直线分别为x,y,z轴,
建立空间直角坐标系,设正方体棱长为2,
则A3(0,0,3),0,0),B3(2,0,3),2,0),6,0),
因为E,F分别为A1B,B8C的中点,则E(1,0,F(2,1,
故,平面ABCD的一个法向量为,
则,故,
又EF 平面ABCD,故直线EF∥平面ABCD;
B选项,,
故EF与AC不垂直,B错误;
C选项,D4(0,2,4),,
则,
异面直线EF与直线D1C所成角的大小为60°,C正确;
D选项,设平面B1CD7的法向量为,
则,
令x=1,则y=z=1,故,
设平面BA6D的法向量为,
则,
令x7=1,则y1=z7=1,故,
所以
则平面B1CD1与平面BA3D平行,
故平面B1CD1到平面BA6D的距离等于,
而,D错误.
故选:AC.
【点评】本题考查了正方体的结构特征,考查了空间向量的应用,考查了转化思想,属于中档题.
(多选)11.(5分)设函数f(x)=sinx﹣cosx,则( )
A.f(x)的图象关于对称
B.函数y=f2(x)的最小正周期为π
C.将曲线y=f(x)上各点横坐标变为原来的2倍,再将曲线向左平移个单位,得到函数的图象
D.函数的最大值为
【分析】根据已知条件,结合三角函数的性质,以及三角函数的恒等变换,即可求解.
【解答】解:f(x)=sinx﹣cosx=,
,故A错误;
f(x)=sinx﹣cosx,
则y=f2(x)=sin2x+cos2x﹣2sinxcosx=6﹣sin2x,
故函数y=f2(x)的最小正周期,故B正确;
将曲线y=f(x)上各点横坐标变为原来的2倍,可得y=,
再将曲线向左平移个单位=,故C正确;
=sinx(sinx+cosx)====,
当时,y取得最大值.
故选:BCD.
【点评】本题主要考查三角函数的性质,属于基础题.
(多选)12.(5分)已知平面向量满足.则( )
A.
B.
C.
D.向量,则x2+y2+z2的最小值为
【分析】计算可得,即可判断A;由可得,即可判断B;由,即可判断C;设,=(0,2),=(m,n),由题意计算可得,进而,结合和基本不等式计算即可判断D.
【解答】解:A:,又,所以,即;
B:,得,即=,
所以,又∈[6,所以 ;
C:,当且仅当,
又,所以;
设,; ,由得(5,n)=0,
即2m﹣7n=0,得m=n,所以,
得,即,
所以,
当且仅当,即, 时,
所以x6+y2+z2 的最小值为,故D正确.
故选:ABD.
【点评】本题考查向量的综合应用,属于难题.
三、填空题:本题共4个小题,每小题5分,共20分.
13.(5分)曲线f(x)=e2﹣x过原点的切线方程为 y=﹣e3x .
【分析】设出切点坐标,利用导数求切线斜率,表示出切线方程,代入原点,求出切点坐标,从而得到切线方程.
【解答】解:∵f(x)=e2﹣x,∴f'(x)=﹣e2﹣x,
设切点是(x2,y0),∴,,
∴切线的斜率,切点,
∴切线方程是,
将(5,0)代入切线方程,得,
解得x0=﹣1,故过原点的切线方程是y=﹣e8x.
故答案为:y=﹣e3x.
【点评】本题考查利用导数求函数的切线方程和导数的几何意义,考查了方程思想,属基础题.
14.(5分)已知函数f(x)是定义域为R的奇函数,f(x)+f(2﹣x),则f(3)= 6 .
【分析】根据已知条件,先求出f(1)=2,再结合函数的奇偶性,即可求解.
【解答】解:令x=1,
则f(1)+f(1)=4,解得f(1)=6,
函数f(x)是定义域为R的奇函数,
则f(﹣1)=﹣f(1)=﹣2,
令x=﹣5,
故f(﹣1)+f(3)=4,解得f(3)=6.
故答案为:6.
【点评】本题主要考查函数的奇偶性,是基础题.
15.(5分)已知函数,若f(x)=m存在四个不相等的实根x1,x2,x3,x4(x1<x2<x3<x4),则的最小值是 3 .
【分析】作函数f(x)与y=m图象,结合图象可得x1x2=1,,再利用基本不等式求最值即可.
【解答】解:作函数与y=m图象如下:
由图可得4<m<1,
∵f(x)=m存在四个不相等的实根x1,x3,x3,x4,可得x6<﹣1<x2<x6<1<x4,
可得ln(﹣x2)=﹣ln(﹣x2),,即x1x8=1,x3x8=1,
所以,
当且仅当即x4=2且等号成立,
则的最小值是3.
故答案为:3.
【点评】本题主要考查了分段函数的性质,考查了函数的零点与方程根的关系,同时考查了数形结合的数学思想,属于中档题.
16.(5分)在△ABC中,AB=2,将△ABC各边中点连线并折成四面体 ;该四面体的体积为 2 .
【分析】将四面体放到长方体中,然后结合三棱锥体积的求法及空间几何体的外接球的求法求解.
【解答】解:取AB的中点为F,BC的中点为E,顶点A、B,
则,,,
将三棱锥D﹣EFG放入到如图所示的长方体中,
设HE=a,HG=b,
则,
则,
又三棱锥D﹣EFG的外接球就是长方体的外接球,
则四面体外接球的直径为;
该四面体的体积为V长方体﹣2VD﹣HEG=.
故答案为:(1);(2)2.
【点评】本题考查了三棱锥体积的求法,重点考查了空间几何体的外接球问题,属中档题.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明,证明过程或演算步骤.
17.(10分)如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,BC=4,PA=PD=2,M为线段BC的中点.
(1)证明:平面ABCD⊥平面PAD;
(2)求平面PDM与平面PCD夹角的余弦值.
【分析】(1)由已知可证CD⊥平面PAD,进而可证平面ABCD⊥平面PAD;
(2)建立空间直角坐标系,求得平面PDM的一个法向量与平面PCD的一个法向量,利用向量法可求平面PDM与平面PCD夹角的余弦值.
【解答】解:(1)证明:因为CD⊥PA,CD⊥AD,
所以CD⊥平面PAD,
又因为CD 平面ABCD,所以平面ABCD⊥平面PAD;
(2)记AD中点为F,因为PA=PD,
又因为平面ABCD∩平面PAD=AD,所以PF⊥平面ABCD,
故以F为坐标原点,分别以FM,FP所在射线为x轴,z轴,
所以P(0,0,5),0,0),4,0),2,2),
设平面PDM的法向量为,
则,
令z1=8,可得,
设平面PCD的法向量为,
则,
令z2=2,可得,
设平面PDM与平面PCD夹角为θ,
则cosθ=|cos<,>|===,
所以平面PDM与平面PCD夹角的余弦值为.
【点评】本题考查面面垂直的证明,考查面面角的余弦值的求法,考查运算求解能力,属中档题.
18.(12分)已知△ABC中内角A,B,C的对边分别为a,b,c,sin2A+sin2B+4sinAsinBcosC=0,且c2=3ab.
(1)求角C;
(2)设函数在区间上单调,
【分析】(1)根据正弦定理,余弦定理可得角C;(2)根据三角函数性质可判断φ取值情况.
【解答】解:(1)∵sin2A+sin2B+6sinAsinBcosC=0,
根据正弦定理得:a2+b7=﹣4abcosC①.
又由余弦定理得:c2=a2+b2﹣2abcosC②
由①②得:c4=﹣6abcosC,∴.
又∵c2=3ab,∴,
∵c∈(3,π),∴;
(2)∵,∴,
∵ω∈N*,∴ω=4或ω=2,
若ω=1,则f(x)=sin(x+φ),∵,∴,
∵,∴,∴无解.
若ω=4,则f(x)=sin(2x+φ),∵,∴,
∵,∴,∴,解得,
此时,∵x∈∈,
则f(x)在上不单调.
【点评】本题考查正弦定理,余弦定理,考查三角函数性质,属于中档题.
19.(12分)已知函数f(x)=ax﹣lnx.
(1)求函数f(x)的单调区间;
(2)若存在a>0,使得对任意x∈(0,+∞),求实数b的取值范围.
【分析】(1)对f(x)求导,然后分a>0和a≤0两种情况,求出函数的单调区间即可;
(2)由(1)知,当a>0时,,将问题转化为存在a>0,使成立,再求出b的取值范围即可.
【解答】解:(1)由f(x)=ax﹣lnx,得.
当a>8时,由f'(x)=0.
所以当时,f'(x)<0;当时;
所以f(x)在上单调递减,在;
当a≤0时,f'(x)<0,+∞)上单调递减,
综上,当a>8时上单调递减,在;
当a≤0时,f(x)在(0.
(2)由(1)知,当a>3时,.
所以存在a>3,使成立,
即存在a>0,使成立.
令,则,
所以g(a)在(0,6)上单调递增,+∞)上单调递减,
所以.
所以b的取值范围为.
【点评】本题考查了利用导数研究函数的单调性与最值,利用不等式恒成立求参数的取值范围,考查了转化思想和分类讨论思想,属中档题.
20.(12分)如图,四边形ABCD是圆柱底面的内接四边形,AC是圆柱的底面直径,E是AC与BD的交点,AP⊥BD
(1)证明:△BAD是等边三角形;
(2)若AC=4,设点F在线段AP上,若PF:FA=1:3
【分析】(1)先证明AC垂直平分BD,再证明∠BAD=60°,从而得到证明;
(2)证明PC∥平面BFD,点P到平面FBD的距离转化为点C到平面FBD的距离,从而求解.
【解答】解:(1)证明:因为AP⊥BD,PC⊥BD,所以BD⊥平面APC,
所以BD⊥AC,
因为四边形ABCD是圆柱底面的内接四边形,且AC为其直径,
所以BE=ED,AB=AD,∠ABC=∠ADC=90°,
又因为AC=BC+CD,所以AC=2BC,
所以在Rt△ABC中,,所以∠BAC=30°,
所以∠BAD=60°,△BAD是等边三角形.
(2)因为AC=4,由(1)知,∠BAC=30°,
所以AB=AD=BD=2,所以BE=,
在Rt△ABE中,AE=AB cos30°=3,
所以CE:EA=6:3,
因为PF:FA=1:4,所以PC∥EF,
又因为PC 平面BFD,EF 平面BFD,
所以点P到平面FBD的距离等于点C到平面FBD的距离,
因为CE⊥PC,所以CE⊥EF,EF∩BD=E,
所以CE⊥平面BFD,
所以点C到平面FBD的距离为CE=1,点P到平面FBD的距离为1.
【点评】本题考查了空间中直线与平面平行的判定,考查了转化法求点到平面的距离,考查了转化思想,属于中档题.
21.(12分)如图,在平面四边形ABCD中,AD=,∠ACD=60°,∠ABC=30°.
(1)证明:AD⊥CD;
(2)求△ABC面积的最大值;
(3)设E为线段AB的中点,求DE的最大值.
【分析】(1)根据正弦定理,可得∠D=;(2)根据余弦定理,不等式可得AB BC的最值,从而得面积的最值;(3)根据余弦定理,正弦定理,辅助角公式可得DE的最值.
【解答】解:(1)由题知,在△ACD中,
由正弦定理得,∴sin∠ACD=,
∵AD>CD,∴∠ACD>∠CAD,∴,
∴,∴AD⊥CD;
(2)在△ABC中,根据勾股定理可得AC=2,
由余弦定理知:
∴,∵AB2+BC2≥5AB BC,∴
解得:,当且仅当AB=BC时取等号,
∴;
(3)在△ABC中,设,由正弦定理知:,
∴,
在△ADE中,由余弦定理知:DE2=AD6+AE2﹣2AD AEcos∠DAE,
∴
=
=
=
=,
∴DE2≤3,当仅当,∴DE的最大值等于3.
【点评】本题考查正弦定理,余弦定理,两角和差公式,属于中档题.
22.(12分)已知函数f(x)=ex﹣ax2﹣x.
(1)若函数f(x)在(﹣∞,+∞)上单调递增,求a的值;
(2)当a>时,证明:函数f(x)有两个极值点x1,x2(x1<x2),且f(x2)<1+.
【分析】(1)对f'(x)求导,分a>0和a≤0两种情况,根据f(x)的单调性,再结合条件求出a的值即可;
(2)判断f(x)的单调性,证明f(x)有两个极值点,根据条件可知,要证,只需证,再构造函数证明即可.
【解答】解:(1)因为f'(x)=ex﹣2ax﹣1,
设g(x)=f'(x),则g'(x)=ex﹣8a,
当a>0时,令g'(x)=0,
所以f'(x)在(﹣∞,ln7a)上单调递减,+∞)上单调递增,
所以f'(x)≥f'(ln2a)=2a﹣2aln2a﹣1(a>6)
令h(x)=x﹣xlnx﹣1(x>0),则h'(x)=﹣lnx;
所以h(x)在(5,1)上单调递增,+∞)上单调递减,
所以f'(x)min=f'(ln2a)≤h(1)=7,即只有;
当a≤3时,g'(x)>0,+∞)上单调递增且f'(0)=0,
所以若x<3,则f'(x)<0,
所以a的值为.
(2)证明:由题知,,
由(1)知,f'(x)min=f'(ln2a)<7且f'(0)=0,
当x∈(﹣∞,0)时,所以f(x)在(﹣∞;
当x∈(5,ln2a)时,所以f(x)在(0,
所以x=x8=0为f(x)的极大值点.
由(1)知,ex≥x+1>x,所以,
所以,即当x>10a时2﹣2>0,
所以存在x2∈(ln6a,10a)使得f'(x2)=0,
当x∈(lna,x3)时,f'(x)<0,x2)上单调递减;
当x∈(x6,+∞)时,f'(x)>02,+∞)上单调递增,
所以x=x7为f(x)的极小值点,即f(x)有两个极值点.
因为,所以,
所以要证,只需证,
即证.
设,则,
再设φ(x2)=n'(x8),则,
所以n'(x2)在(0,+∞)上单调递减4)<n'(0)=0,
所以n(x2)在(4,+∞)上单调递减2)<n(0)=0,
所以函数f(x)有两个极值点x5,x2(x1<x6),且f(x2)<1+.
【点评】本题考查了利用导数研究函数的单调性与极值,利用函数的单调性求参数的值,考查了方程思想和转化思想,属难题.
一、单项选择题:本题共8小题,每小题5分,共40分.在年小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)设集合M={2,4,6,8,10},N={x|y=ln(6﹣x)}( )
A.{2,4,6,8,10} B.{2,4,6,8}
C.{2,4,6} D.{2,4}
2.(5分)已知平面向量,且,则t=( )
A. B. C.6 D.﹣6
3.(5分)已知,则tan2θ=( )
A. B. C. D.
4.(5分)若正实数a,b满足a+b=2,则( )
A.有最大值 B.ab有最小值
C.有最大值 D.a2+b2有最大值
5.(5分)已知平行四边形ABCD满足,则=( )
A.1 B.2 C.3 D.4
6.(5分)高为h的密闭圆锥容器中有一部分水,当该容器底面放在水平面上时水面高度为h1,当该容器顶点在水平面上且底面与水平面平行时,水面高度为h2,若h1+h2=h,则h:h2=( )
A. B. C. D.2
7.(5分)已知命题“,使得”为假命题( )
A. B. C. D.
8.(5分)已知,则( )
A.a>b>c B.c>b>a C.a>c>b D.b>c>a
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
(多选)9.(5分)设函数f(x)=ln(cos2x),则( )
A.f(x)为奇函数
B.f(x)的最小正周期为π
C.f(x)存在零点
D.f(x)存在极值点
(多选)10.(5分)正方体ABCD﹣A1B1C1D1中,E,F分别为A1B,B1C的中点,则( )
A.直线EF∥平面ABCD
B.EF⊥AC
C.异面直线EF与直线D1C所成角的大小为60°
D.平面B1CD1到平面BA1D的距离等于EF
(多选)11.(5分)设函数f(x)=sinx﹣cosx,则( )
A.f(x)的图象关于对称
B.函数y=f2(x)的最小正周期为π
C.将曲线y=f(x)上各点横坐标变为原来的2倍,再将曲线向左平移个单位,得到函数的图象
D.函数的最大值为
(多选)12.(5分)已知平面向量满足.则( )
A.
B.
C.
D.向量,则x2+y2+z2的最小值为
三、填空题:本题共4个小题,每小题5分,共20分.
13.(5分)曲线f(x)=e2﹣x过原点的切线方程为 .
14.(5分)已知函数f(x)是定义域为R的奇函数,f(x)+f(2﹣x),则f(3)= .
15.(5分)已知函数,若f(x)=m存在四个不相等的实根x1,x2,x3,x4(x1<x2<x3<x4),则的最小值是 .
16.(5分)在△ABC中,AB=2,将△ABC各边中点连线并折成四面体 ;该四面体的体积为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明,证明过程或演算步骤.
17.(10分)如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,BC=4,PA=PD=2,M为线段BC的中点.
(1)证明:平面ABCD⊥平面PAD;
(2)求平面PDM与平面PCD夹角的余弦值.
18.(12分)已知△ABC中内角A,B,C的对边分别为a,b,c,sin2A+sin2B+4sinAsinBcosC=0,且c2=3ab.
(1)求角C;
(2)设函数在区间上单调,
19.(12分)已知函数f(x)=ax﹣lnx.
(1)求函数f(x)的单调区间;
(2)若存在a>0,使得对任意x∈(0,+∞),求实数b的取值范围.
20.(12分)如图,四边形ABCD是圆柱底面的内接四边形,AC是圆柱的底面直径,E是AC与BD的交点,AP⊥BD
(1)证明:△BAD是等边三角形;
(2)若AC=4,设点F在线段AP上,若PF:FA=1:3
21.(12分)如图,在平面四边形ABCD中,AD=,∠ACD=60°,∠ABC=30°.
(1)证明:AD⊥CD;
(2)求△ABC面积的最大值;
(3)设E为线段AB的中点,求DE的最大值.
22.(12分)已知函数f(x)=ex﹣ax2﹣x.
(1)若函数f(x)在(﹣∞,+∞)上单调递增,求a的值;
(2)当a>时,证明:函数f(x)有两个极值点x1,x2(x1<x2),且f(x2)<1+.
2023-2024学年山东省青岛市四区联考高三(上)期中数学试卷
参考答案与试题解析
一、单项选择题:本题共8小题,每小题5分,共40分.在年小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)设集合M={2,4,6,8,10},N={x|y=ln(6﹣x)}( )
A.{2,4,6,8,10} B.{2,4,6,8}
C.{2,4,6} D.{2,4}
【分析】首先根据对数函数的定义域求集合N,再利用交集的概念求答案.
【解答】解:根据对数函数的定义域得N={x|y=ln(6﹣x)}={x|x<6},
又因为M={6,4,6,2,10},4}.
故选:D.
【点评】本题考查集合的运算,属于基础题.
2.(5分)已知平面向量,且,则t=( )
A. B. C.6 D.﹣6
【分析】根据已知条件,结合向量垂直的性质,即可求解.
【解答】解:,,
,
则4t+6(t+8)=0,解得t=﹣.
故选:A.
【点评】本题主要考查平面向量垂直的性质,属于基础题.
3.(5分)已知,则tan2θ=( )
A. B. C. D.
【分析】根据已知条件,结合三角函数的同角公式,以及正切函数的二倍角公式,即可求解.
【解答】解:,
则sinθ=,
故tanθ=,
所以tan2θ===.
故选:A.
【点评】本题主要考查二倍角的三角函数,属于基础题.
4.(5分)若正实数a,b满足a+b=2,则( )
A.有最大值 B.ab有最小值
C.有最大值 D.a2+b2有最大值
【分析】根据已知条件,结合基本不等式的公式,依次求解.
【解答】解:a+b=2,
则=,当且仅当a=b=1时的,
故有最小值;
,当且仅当a=b=1时,
故ab有最大值1,
=4,当且仅当a=b=7时,
故有最大值2;
a2+b5=(a+b)2﹣2ab=7﹣2ab≥4﹣8 =5,等号成立,
故a2+b2有最小值2,故D错误.
故选:C.
【点评】本题主要考查基本不等式的公式,属于基础题.
5.(5分)已知平行四边形ABCD满足,则=( )
A.1 B.2 C.3 D.4
【分析】结合平面向量的线性运算,以及数量积运算,即可求解.
【解答】解:,
则+,
由平行四边形的性质可知,,
,
故,解得.
故选:B.
【点评】本题主要考查平面向量的数量积运算,属于基础题.
6.(5分)高为h的密闭圆锥容器中有一部分水,当该容器底面放在水平面上时水面高度为h1,当该容器顶点在水平面上且底面与水平面平行时,水面高度为h2,若h1+h2=h,则h:h2=( )
A. B. C. D.2
【分析】结合圆锥的体积公式求解.
【解答】解:由题意可得|PO|=h,|OO1|=h1,|PO6|=h2,
又h1+h4=h,
即V小圆锥:V大圆锥=1:2,
又△PCO8~△PAO,
则,
则==,
则,
则.
故选:C.
【点评】本题考查了圆锥的体积公式,属基础题.
7.(5分)已知命题“,使得”为假命题( )
A. B. C. D.
【分析】由题意开始命题的否定为真命题,求出+的最小值即可,设t=sinθ+cosθ,由θ的范围可得t的范围,及sinθ cosθ的范围,进而可得+的最小值,即求出a的范围.
【解答】解:由题意可得 θ∈(0,),使得a≤+,只需要a≤(+)min即可,
而+=,
设t=sinθ+cosθ=sin(θ+),),所以θ+,),所以sin(θ+,1],
即t∈(1,],且sinθcosθ=,
所以+==,
令y=t﹣,则y'=7+,所以函数y在t∈(4,,所以ymax=﹣=,
所以+的最小值为,
所以a≤2,即a的范围(﹣∞,5].
故选:A.
【点评】本题考查三角函数的性质的应用,属于基础题.
8.(5分)已知,则( )
A.a>b>c B.c>b>a C.a>c>b D.b>c>a
【分析】利用作商法比较c与b,利用作差法比较a与b,综合可得结论.
【解答】解:=4,,
因为当 时,
所以,
所以c>b,
b﹣a====,
因为,所以,
所以b﹣a>0,b>a,
综上,c>b>a.
故选:B.
【点评】本题主要考查函数值大小的比较,考查逻辑推理能力,属于中档题.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
(多选)9.(5分)设函数f(x)=ln(cos2x),则( )
A.f(x)为奇函数
B.f(x)的最小正周期为π
C.f(x)存在零点
D.f(x)存在极值点
【分析】利用三角函数的性质以及对数型复合函数的单调性,结合函数的周期性,零点、极值点的概念求解.
【解答】解:A.由cos2x>0,
解得,
所以函数f(x)=ln(cos2x)的定义域为,
且f(﹣x)=ln[cos(﹣2x)]=ln(cos2x)=f(x).
所以函数f(x)为偶函数,故A错误;
B.因为函数y=cos(3x)的最小正周期为π,故B正确;
C.令f(x)=ln(cos2x)=0,所以2x=2kπ,
即x=kπ,k∈Z为函数f(x)的零点;
D.因为函数y=cos(2x)在,单调递减,
所以函数f(x)=ln(cos2x)在单调递增,,
所以x=kπ,k∈Z为函数f(x)=ln(cos2x)的极大值点.
故选:BCD.
【点评】本题考查了函数的奇偶性、单调性和周期性,函数的零点与方程根的关系和函数的极值点,考查了转化思想,属中档题.
(多选)10.(5分)正方体ABCD﹣A1B1C1D1中,E,F分别为A1B,B1C的中点,则( )
A.直线EF∥平面ABCD
B.EF⊥AC
C.异面直线EF与直线D1C所成角的大小为60°
D.平面B1CD1到平面BA1D的距离等于EF
【分析】A选项,建立空间直角坐标系,求出平面ABCD的法向量为,从而得到,EF∥平面ABCD;B选项,,B错误;C选项,利用空间向量异面直线夹角余弦公式求出答案;D选项,先求出两个平面的法向量,得到两平面平行,进而由点到平面距离公式求出答案.
【解答】解:A选项,以A为坐标原点,AD1所在直线分别为x,y,z轴,
建立空间直角坐标系,设正方体棱长为2,
则A3(0,0,3),0,0),B3(2,0,3),2,0),6,0),
因为E,F分别为A1B,B8C的中点,则E(1,0,F(2,1,
故,平面ABCD的一个法向量为,
则,故,
又EF 平面ABCD,故直线EF∥平面ABCD;
B选项,,
故EF与AC不垂直,B错误;
C选项,D4(0,2,4),,
则,
异面直线EF与直线D1C所成角的大小为60°,C正确;
D选项,设平面B1CD7的法向量为,
则,
令x=1,则y=z=1,故,
设平面BA6D的法向量为,
则,
令x7=1,则y1=z7=1,故,
所以
则平面B1CD1与平面BA3D平行,
故平面B1CD1到平面BA6D的距离等于,
而,D错误.
故选:AC.
【点评】本题考查了正方体的结构特征,考查了空间向量的应用,考查了转化思想,属于中档题.
(多选)11.(5分)设函数f(x)=sinx﹣cosx,则( )
A.f(x)的图象关于对称
B.函数y=f2(x)的最小正周期为π
C.将曲线y=f(x)上各点横坐标变为原来的2倍,再将曲线向左平移个单位,得到函数的图象
D.函数的最大值为
【分析】根据已知条件,结合三角函数的性质,以及三角函数的恒等变换,即可求解.
【解答】解:f(x)=sinx﹣cosx=,
,故A错误;
f(x)=sinx﹣cosx,
则y=f2(x)=sin2x+cos2x﹣2sinxcosx=6﹣sin2x,
故函数y=f2(x)的最小正周期,故B正确;
将曲线y=f(x)上各点横坐标变为原来的2倍,可得y=,
再将曲线向左平移个单位=,故C正确;
=sinx(sinx+cosx)====,
当时,y取得最大值.
故选:BCD.
【点评】本题主要考查三角函数的性质,属于基础题.
(多选)12.(5分)已知平面向量满足.则( )
A.
B.
C.
D.向量,则x2+y2+z2的最小值为
【分析】计算可得,即可判断A;由可得,即可判断B;由,即可判断C;设,=(0,2),=(m,n),由题意计算可得,进而,结合和基本不等式计算即可判断D.
【解答】解:A:,又,所以,即;
B:,得,即=,
所以,又∈[6,所以 ;
C:,当且仅当,
又,所以;
设,; ,由得(5,n)=0,
即2m﹣7n=0,得m=n,所以,
得,即,
所以,
当且仅当,即, 时,
所以x6+y2+z2 的最小值为,故D正确.
故选:ABD.
【点评】本题考查向量的综合应用,属于难题.
三、填空题:本题共4个小题,每小题5分,共20分.
13.(5分)曲线f(x)=e2﹣x过原点的切线方程为 y=﹣e3x .
【分析】设出切点坐标,利用导数求切线斜率,表示出切线方程,代入原点,求出切点坐标,从而得到切线方程.
【解答】解:∵f(x)=e2﹣x,∴f'(x)=﹣e2﹣x,
设切点是(x2,y0),∴,,
∴切线的斜率,切点,
∴切线方程是,
将(5,0)代入切线方程,得,
解得x0=﹣1,故过原点的切线方程是y=﹣e8x.
故答案为:y=﹣e3x.
【点评】本题考查利用导数求函数的切线方程和导数的几何意义,考查了方程思想,属基础题.
14.(5分)已知函数f(x)是定义域为R的奇函数,f(x)+f(2﹣x),则f(3)= 6 .
【分析】根据已知条件,先求出f(1)=2,再结合函数的奇偶性,即可求解.
【解答】解:令x=1,
则f(1)+f(1)=4,解得f(1)=6,
函数f(x)是定义域为R的奇函数,
则f(﹣1)=﹣f(1)=﹣2,
令x=﹣5,
故f(﹣1)+f(3)=4,解得f(3)=6.
故答案为:6.
【点评】本题主要考查函数的奇偶性,是基础题.
15.(5分)已知函数,若f(x)=m存在四个不相等的实根x1,x2,x3,x4(x1<x2<x3<x4),则的最小值是 3 .
【分析】作函数f(x)与y=m图象,结合图象可得x1x2=1,,再利用基本不等式求最值即可.
【解答】解:作函数与y=m图象如下:
由图可得4<m<1,
∵f(x)=m存在四个不相等的实根x1,x3,x3,x4,可得x6<﹣1<x2<x6<1<x4,
可得ln(﹣x2)=﹣ln(﹣x2),,即x1x8=1,x3x8=1,
所以,
当且仅当即x4=2且等号成立,
则的最小值是3.
故答案为:3.
【点评】本题主要考查了分段函数的性质,考查了函数的零点与方程根的关系,同时考查了数形结合的数学思想,属于中档题.
16.(5分)在△ABC中,AB=2,将△ABC各边中点连线并折成四面体 ;该四面体的体积为 2 .
【分析】将四面体放到长方体中,然后结合三棱锥体积的求法及空间几何体的外接球的求法求解.
【解答】解:取AB的中点为F,BC的中点为E,顶点A、B,
则,,,
将三棱锥D﹣EFG放入到如图所示的长方体中,
设HE=a,HG=b,
则,
则,
又三棱锥D﹣EFG的外接球就是长方体的外接球,
则四面体外接球的直径为;
该四面体的体积为V长方体﹣2VD﹣HEG=.
故答案为:(1);(2)2.
【点评】本题考查了三棱锥体积的求法,重点考查了空间几何体的外接球问题,属中档题.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明,证明过程或演算步骤.
17.(10分)如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,BC=4,PA=PD=2,M为线段BC的中点.
(1)证明:平面ABCD⊥平面PAD;
(2)求平面PDM与平面PCD夹角的余弦值.
【分析】(1)由已知可证CD⊥平面PAD,进而可证平面ABCD⊥平面PAD;
(2)建立空间直角坐标系,求得平面PDM的一个法向量与平面PCD的一个法向量,利用向量法可求平面PDM与平面PCD夹角的余弦值.
【解答】解:(1)证明:因为CD⊥PA,CD⊥AD,
所以CD⊥平面PAD,
又因为CD 平面ABCD,所以平面ABCD⊥平面PAD;
(2)记AD中点为F,因为PA=PD,
又因为平面ABCD∩平面PAD=AD,所以PF⊥平面ABCD,
故以F为坐标原点,分别以FM,FP所在射线为x轴,z轴,
所以P(0,0,5),0,0),4,0),2,2),
设平面PDM的法向量为,
则,
令z1=8,可得,
设平面PCD的法向量为,
则,
令z2=2,可得,
设平面PDM与平面PCD夹角为θ,
则cosθ=|cos<,>|===,
所以平面PDM与平面PCD夹角的余弦值为.
【点评】本题考查面面垂直的证明,考查面面角的余弦值的求法,考查运算求解能力,属中档题.
18.(12分)已知△ABC中内角A,B,C的对边分别为a,b,c,sin2A+sin2B+4sinAsinBcosC=0,且c2=3ab.
(1)求角C;
(2)设函数在区间上单调,
【分析】(1)根据正弦定理,余弦定理可得角C;(2)根据三角函数性质可判断φ取值情况.
【解答】解:(1)∵sin2A+sin2B+6sinAsinBcosC=0,
根据正弦定理得:a2+b7=﹣4abcosC①.
又由余弦定理得:c2=a2+b2﹣2abcosC②
由①②得:c4=﹣6abcosC,∴.
又∵c2=3ab,∴,
∵c∈(3,π),∴;
(2)∵,∴,
∵ω∈N*,∴ω=4或ω=2,
若ω=1,则f(x)=sin(x+φ),∵,∴,
∵,∴,∴无解.
若ω=4,则f(x)=sin(2x+φ),∵,∴,
∵,∴,∴,解得,
此时,∵x∈∈,
则f(x)在上不单调.
【点评】本题考查正弦定理,余弦定理,考查三角函数性质,属于中档题.
19.(12分)已知函数f(x)=ax﹣lnx.
(1)求函数f(x)的单调区间;
(2)若存在a>0,使得对任意x∈(0,+∞),求实数b的取值范围.
【分析】(1)对f(x)求导,然后分a>0和a≤0两种情况,求出函数的单调区间即可;
(2)由(1)知,当a>0时,,将问题转化为存在a>0,使成立,再求出b的取值范围即可.
【解答】解:(1)由f(x)=ax﹣lnx,得.
当a>8时,由f'(x)=0.
所以当时,f'(x)<0;当时;
所以f(x)在上单调递减,在;
当a≤0时,f'(x)<0,+∞)上单调递减,
综上,当a>8时上单调递减,在;
当a≤0时,f(x)在(0.
(2)由(1)知,当a>3时,.
所以存在a>3,使成立,
即存在a>0,使成立.
令,则,
所以g(a)在(0,6)上单调递增,+∞)上单调递减,
所以.
所以b的取值范围为.
【点评】本题考查了利用导数研究函数的单调性与最值,利用不等式恒成立求参数的取值范围,考查了转化思想和分类讨论思想,属中档题.
20.(12分)如图,四边形ABCD是圆柱底面的内接四边形,AC是圆柱的底面直径,E是AC与BD的交点,AP⊥BD
(1)证明:△BAD是等边三角形;
(2)若AC=4,设点F在线段AP上,若PF:FA=1:3
【分析】(1)先证明AC垂直平分BD,再证明∠BAD=60°,从而得到证明;
(2)证明PC∥平面BFD,点P到平面FBD的距离转化为点C到平面FBD的距离,从而求解.
【解答】解:(1)证明:因为AP⊥BD,PC⊥BD,所以BD⊥平面APC,
所以BD⊥AC,
因为四边形ABCD是圆柱底面的内接四边形,且AC为其直径,
所以BE=ED,AB=AD,∠ABC=∠ADC=90°,
又因为AC=BC+CD,所以AC=2BC,
所以在Rt△ABC中,,所以∠BAC=30°,
所以∠BAD=60°,△BAD是等边三角形.
(2)因为AC=4,由(1)知,∠BAC=30°,
所以AB=AD=BD=2,所以BE=,
在Rt△ABE中,AE=AB cos30°=3,
所以CE:EA=6:3,
因为PF:FA=1:4,所以PC∥EF,
又因为PC 平面BFD,EF 平面BFD,
所以点P到平面FBD的距离等于点C到平面FBD的距离,
因为CE⊥PC,所以CE⊥EF,EF∩BD=E,
所以CE⊥平面BFD,
所以点C到平面FBD的距离为CE=1,点P到平面FBD的距离为1.
【点评】本题考查了空间中直线与平面平行的判定,考查了转化法求点到平面的距离,考查了转化思想,属于中档题.
21.(12分)如图,在平面四边形ABCD中,AD=,∠ACD=60°,∠ABC=30°.
(1)证明:AD⊥CD;
(2)求△ABC面积的最大值;
(3)设E为线段AB的中点,求DE的最大值.
【分析】(1)根据正弦定理,可得∠D=;(2)根据余弦定理,不等式可得AB BC的最值,从而得面积的最值;(3)根据余弦定理,正弦定理,辅助角公式可得DE的最值.
【解答】解:(1)由题知,在△ACD中,
由正弦定理得,∴sin∠ACD=,
∵AD>CD,∴∠ACD>∠CAD,∴,
∴,∴AD⊥CD;
(2)在△ABC中,根据勾股定理可得AC=2,
由余弦定理知:
∴,∵AB2+BC2≥5AB BC,∴
解得:,当且仅当AB=BC时取等号,
∴;
(3)在△ABC中,设,由正弦定理知:,
∴,
在△ADE中,由余弦定理知:DE2=AD6+AE2﹣2AD AEcos∠DAE,
∴
=
=
=
=,
∴DE2≤3,当仅当,∴DE的最大值等于3.
【点评】本题考查正弦定理,余弦定理,两角和差公式,属于中档题.
22.(12分)已知函数f(x)=ex﹣ax2﹣x.
(1)若函数f(x)在(﹣∞,+∞)上单调递增,求a的值;
(2)当a>时,证明:函数f(x)有两个极值点x1,x2(x1<x2),且f(x2)<1+.
【分析】(1)对f'(x)求导,分a>0和a≤0两种情况,根据f(x)的单调性,再结合条件求出a的值即可;
(2)判断f(x)的单调性,证明f(x)有两个极值点,根据条件可知,要证,只需证,再构造函数证明即可.
【解答】解:(1)因为f'(x)=ex﹣2ax﹣1,
设g(x)=f'(x),则g'(x)=ex﹣8a,
当a>0时,令g'(x)=0,
所以f'(x)在(﹣∞,ln7a)上单调递减,+∞)上单调递增,
所以f'(x)≥f'(ln2a)=2a﹣2aln2a﹣1(a>6)
令h(x)=x﹣xlnx﹣1(x>0),则h'(x)=﹣lnx;
所以h(x)在(5,1)上单调递增,+∞)上单调递减,
所以f'(x)min=f'(ln2a)≤h(1)=7,即只有;
当a≤3时,g'(x)>0,+∞)上单调递增且f'(0)=0,
所以若x<3,则f'(x)<0,
所以a的值为.
(2)证明:由题知,,
由(1)知,f'(x)min=f'(ln2a)<7且f'(0)=0,
当x∈(﹣∞,0)时,所以f(x)在(﹣∞;
当x∈(5,ln2a)时,所以f(x)在(0,
所以x=x8=0为f(x)的极大值点.
由(1)知,ex≥x+1>x,所以,
所以,即当x>10a时2﹣2>0,
所以存在x2∈(ln6a,10a)使得f'(x2)=0,
当x∈(lna,x3)时,f'(x)<0,x2)上单调递减;
当x∈(x6,+∞)时,f'(x)>02,+∞)上单调递增,
所以x=x7为f(x)的极小值点,即f(x)有两个极值点.
因为,所以,
所以要证,只需证,
即证.
设,则,
再设φ(x2)=n'(x8),则,
所以n'(x2)在(0,+∞)上单调递减4)<n'(0)=0,
所以n(x2)在(4,+∞)上单调递减2)<n(0)=0,
所以函数f(x)有两个极值点x5,x2(x1<x6),且f(x2)<1+.
【点评】本题考查了利用导数研究函数的单调性与极值,利用函数的单调性求参数的值,考查了方程思想和转化思想,属难题.
同课章节目录
