第1章 有理数 期末单元综合复习题 (辽宁地区适用)(含解析)——2023-2024学年上学期人教版七年级数学
文档属性
| 名称 | 第1章 有理数 期末单元综合复习题 (辽宁地区适用)(含解析)——2023-2024学年上学期人教版七年级数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 676.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 00:00:00 | ||
图片预览




文档简介
第1章 有理数
一、单选题
1.(2023上·辽宁锦州·七年级统考期末)的相反数是( )
A. B. C. D.
2.(2023上·辽宁鞍山·七年级统考期末)某年我国人均水资源比上年的增幅是,后续三年各年比上年的增幅分别是,,,这些增幅中最小的是( )
A. B. C.13.0% D.
3.(2023上·辽宁锦州·七年级统考期末)我国是最早进行负数运算的国家,魏晋时期的数学家刘徽在其著作《九章算术注》中,用不同颜色的算筹《小棍形状的记数工具)分别表示正数和负数(白色为正,黑色为负),如图表示的是的计算过程,则图表示的计算过程是( )
A. B.
C. D.
4.(2023上·辽宁沈阳·七年级统考期末)如图是某市11月份连续四天的天气预报信息,其中日温差最大的一天是( )
11月11日 11月12日 11月13日 11月14日
多云 南风级 阵雨 北风级 阵雨 北风级 晴 西北风级
A.11月11日 B.11月12日 C.11月13日 D.11月14日
5.(2021上·辽宁盘锦·七年级统考期末)珠穆朗玛峰海拔高8848米,塔里木盆地海拔高—153米,求珠穆朗玛峰比塔里木盆地,高多少米列式正确的是( )
A.8848+153 B.8848+(-153)
C.8848-153 D.8848-(-153)
6.(2023上·辽宁锦州·七年级统考期末)如图,数轴上三点表示的有理数分别为,下列四个结论:①;②;③;④.其中正确结论的序号为( )
A.①②③ B.①②④ C.①③④ D.②③④
7.(2023上·辽宁葫芦岛·七年级统考期末)有理数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )
A. B. C. D.
8.(2023上·辽宁沈阳·七年级统考期末)下列说法正确的是( )
A.有理数的绝对值一定比0大
B.有理数的相反数一定比0小
C.如果两个数的绝对值相等,那么这两个数相等
D.乘积为1的两个数互为倒数
9.(2023上·辽宁辽阳·七年级统考期末)在,,,中,负数的个数是( )
A.4个 B.3个 C.2个 D.1个
10.(2023上·辽宁锦州·七年级统考期末)习近平总书记在中国共产党第二十次全国代表大会上的报告中指出:十年来,我国经济实力实现历史性跃升,国内生产总值从54万亿元增长到114万亿元,我国经济总量占世界经济的比重达18.5%,提高7.2个百分点,稳居世界第二位.数据114万亿用科学记数法表示为( )
A. B. C. D.
11.(2023上·辽宁葫芦岛·七年级统考期末)2022年我国新能源汽车保有量达辆,同比增长.请将用科学记数法表示为( )
A. B. C. D.
二、填空题
12.(2023上·辽宁葫芦岛·七年级统考期末)升降机在运行过程中,如果上升15米记作“+15米”,那么下降3米记作 米.
13.(2023上·辽宁沈阳·七年级统考期末)如图,数轴上点A,B,C,D表示的数分别为a,b,c,d,相邻两点间的距离均为2个单位长度.
(1)若a与c互为相反数,则 ;
(2)若这四个数中最小数与最大数的和等于10,则 .
14.(2023上·辽宁抚顺·七年级统考期末)计算:= .
15.(2023上·辽宁沈阳·七年级统考期末)计算: .
16.(2022·广西玉林·统考中考真题)计算: .
三、解答题
17.(2023上·辽宁沈阳·七年级统考期末)将下列各数填入所属的集合中:
0,,,,,3.5,0.6,,10,,,6.5
正数集合:{ …};
整数集合:{ …};
分数集合:{ …};
负整数集合:{ …};
正分数集合:{ …};
18.(2023上·辽宁抚顺·七年级统考期末)已知点A在数轴上的对应的数为a,点B对应的数为b,且满足.
(1)点A到点B的距离为_________;
(2)如图,点P是数轴上一点,点P到点A的距离是点P到点B的距离的3倍(即),求点P在数轴上对应的数.
19.(2023上·辽宁沈阳·七年级统考期末)(1)把6.5,,0,3,,表示在数轴上.
(2)请将上面的数用“<”连接起来;
(3)观察数轴,直接写出绝对值小于的所有整数.
20.(2023上·辽宁鞍山·七年级统考期末)阅读材料并回答问题:
的含义是数轴上表示数的点与原点的距离,即,也就是说,表示在数轴上数与数0对应的点之间的距离;因此可以推断表示在数轴上数与数1对应的点之间的距离.例如,,就是在数轴上到1的距离为2的点对应的数,即为或;回答问题:
(1)若,则的值是______;
(2)利用上述方法解下列方程:①;②
21.(2023上·辽宁抚顺·七年级统考期末)“新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩加工厂为满足市场需求,计划在本周每日生产个医用口罩,但是由于各种原因,实际每日生产量与计划每日生产量相比情况如下表(增加的口罩数为正数,减少的口罩数为负数):
星期 一 二 三 四 五 六 日
增减(单位:个)
(1)本周产量最多的一日生产了 个口罩;
(2)本周产量最少的一日生产了 个口罩;
(3)请你根据记录求出本周实际共生产多少个口罩?
22.(2023上·辽宁葫芦岛·七年级统考期末)式子“”表示从1开始的连续100个正整数的和,由于上述式子比较长,书写不方便,为了简便起见,可以将上述式子表示为,这里“”是求和的符号.例如“”用“”可以表示为;“.”用“”可以表示为.
(1)把写成加法的形式是______;
(2)“”用“”可以表示为______;
(3)计算:.
23.(2023上·辽宁辽阳·七年级统考期末)计算:
(1);
(2).
24.(2023上·辽宁朝阳·七年级统考期末)计算:
(1)
(2)
25.(2023上·辽宁抚顺·七年级统考期末)某空军举行特技飞行表演,其中一架飞机起飞0.5千米后的高度变化如下表:(“+”表示上升,“﹣”表示下降)
(1)完成表格;
高度变化 此刻高度记作
____
____
____
(2)飞机完成上述四个表演动作后,飞机高度是多少千米?
(3)如果飞机每上升1千米需消耗5升燃油,平均每下降1千米需消耗3升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
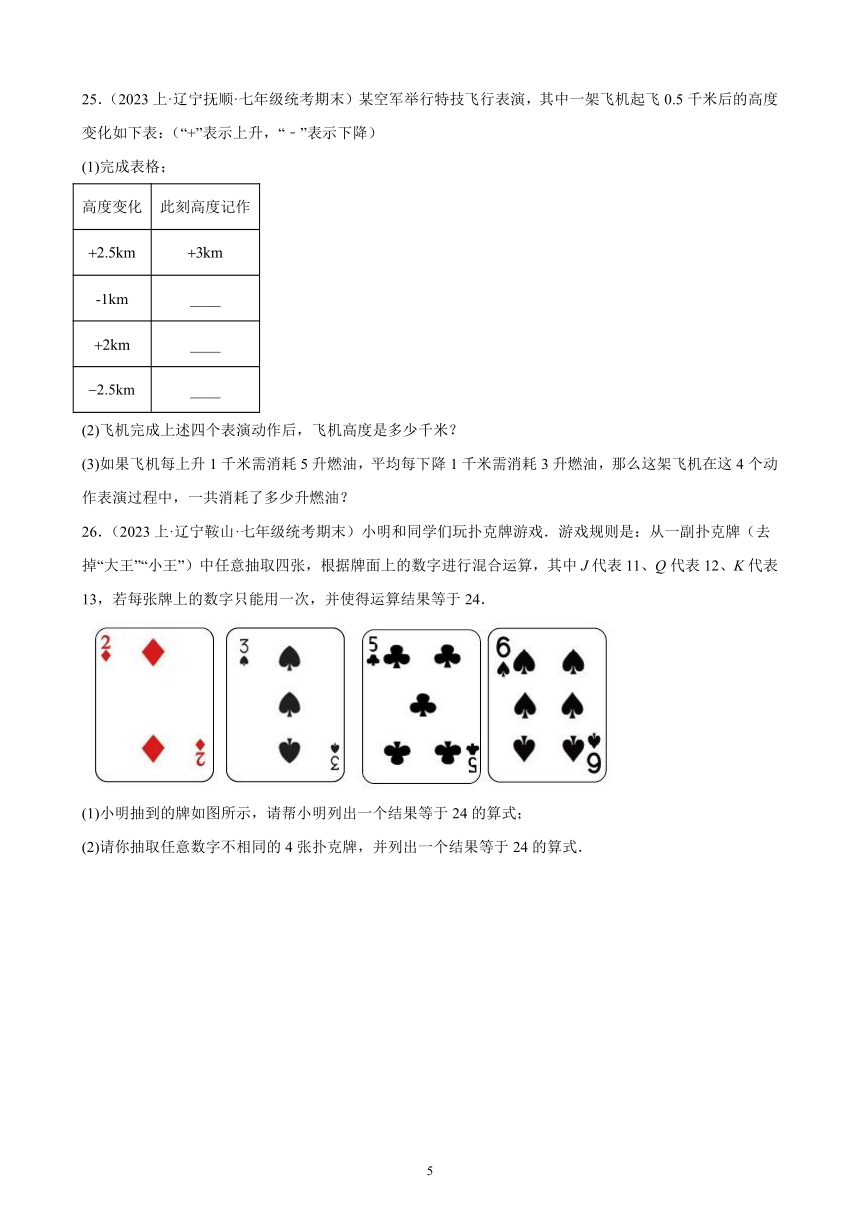
26.(2023上·辽宁鞍山·七年级统考期末)小明和同学们玩扑克牌游戏.游戏规则是:从一副扑克牌(去掉“大王”“小王”)中任意抽取四张,根据牌面上的数字进行混合运算,其中J代表11、Q代表12、K代表13,若每张牌上的数字只能用一次,并使得运算结果等于24.
(1)小明抽到的牌如图所示,请帮小明列出一个结果等于24的算式;
(2)请你抽取任意数字不相同的4张扑克牌,并列出一个结果等于24的算式.
参考答案:
1.D
【分析】只有符号不同的两个数叫做互为相反数,由此即可得到答案.
【详解】解:的相反数是.
故选:D.
【点睛】本题考查相反数,解题的关键是掌握相反数的定义.
2.D
【分析】根据有理数的大小得出结论即可.
【详解】解:,
故选:D.
【点睛】本题主要考查有理数大小的比较,熟练掌握有理数大小比较的方法是解题的关键.
3.A
【分析】通过观察图找到计算的过程与规律,类比图即可得出答案.
【详解】解:根据题意可知:一横表示,一竖表示,
通过观察,可知图和图的计算过程相同,只是数值的不同,
∴图中表示的计算过程是:,
故选:A.
【点睛】本题考查正数和负数,有理数的加法运算,解题关键能够类比题干中的信息从而解决问题.
4.C
【分析】分别求出每天的温差,然后进行比较即可.
【详解】解:11月11日温差为,
11月12日温差为,
11月13日温差为,
11月14日温差为,
∵,
∴日温差最大的一天是11月13日,故C正确.
故选:C.
【点睛】本题主要考查了有理数减法的应用,解题的关键是准确求出四天的温差.
5.D
【分析】直接用珠穆朗玛峰的海拔高度减去塔里木盆地的海拔高度即可表示.
【详解】,
故选:D.
【点睛】本题考查有理数减法的实际应用,理解用较大的数减去较小的数表示差值是解题关键.
6.B
【分析】根据即可判断①,根据即可判断②,根据,即可判断③,根据,即可判断④.
【详解】解:由题意可得,,
∴,故①正确;
∵,
∴,故②正确;
∵,,
∴,故③错误;
∵,,
∴,故④正确,
综上可知,正确结论是①②④,
故选:B
【点睛】此题考查了根据点在数轴上的位置判断式子的符号,熟练掌握有理数的运算法则是解题的关键.
7.C
【分析】由数轴可知,,,则,,据此逐一判断,即可得到答案.
【详解】解:由数轴可知,,,则,,
A、,原结论错误,不符合题意,选项错误;
B、,原结论错误,不符合题意,选项错误;
C、,原结论正确,符合题意,选项正确;
D、,原结论错误,不符合题意,选项错误;
故选:C.
【点睛】本题考查了数轴,有理数的加法、减法和乘法,熟练掌握数轴上点的特征是解题关键.
8.D
【分析】根据绝对值的非负性,相反数的定义,倒数的定义,逐一进行判断即可.
【详解】解:A、有理数的绝对值一定大于等于0,选项错误,不符合题意;
B、正有理数的相反数一定比0小,选项错误,不符合题意;
C、如果两个数的绝对值相等,那么这两个数相等或互为相反数,选项错误,不符合题意;
D、乘积为1的两个数互为倒数,选项正确,符合题意;
故选D.
【点睛】本题考查绝对值的意义,相反数和倒数.熟练掌握相关知识点,是解题的关键.
9.B
【分析】先将各数化简,然后根据负数的概念判断即可.
【详解】解:,,,
∴负数的个数是3.
故选B.
【点睛】本题主要考查多重符号的化简,乘方的运算以及绝对值的化简,熟练掌握计算方法是解决本题的关键.
10.C
【分析】科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正整数;当原数的绝对值时,n是负整数.
【详解】解:114万亿,
故选:C.
【点睛】本题主要考查科学记数法.科学记数法的表示形式为的形式,其中,n为整数.解题关键是正确确定a的值以及n的值.
11.C
【分析】用科学记数法表示较大的数时,一般形式为,其中,为整数,且比原来的整数位数少1,据此判断即可.
【详解】解:.
故选:C.
【点睛】本题考查了用科学记数法表示较大的数,一般形式为,其中,确定与的值是解本题的关键.
12.
【分析】根据升降机运行的过程中,如果上升米记作“米”,可以得到下降米应记作负数.
【详解】解:升降机运行的过程中,如果上升米记作“米”,那么下降3米应记作米.
故答案为:.
【点睛】本题考查了正数和负数的实际应用,掌握正数和负数的含义是解题的关键.
13. 4 2
【分析】(1)根据a与c互为相反数,知道点B是原点,根据相邻两点间的距离均为2个单位长度得到d的值;
(2)根据这四个数中最小数与最大数的和等于10,得到,由,得到一元一次方程,解方程即可得出答案.
【详解】(1)解:∵a与c互为相反数,
∴,,,,
故答案为:4;
(2)解:∵这四个数中最小数与最大数的和等于10,
∴,
∵相邻两点间的距离均为2个单位长度.
∴,即,
∴,
∴.
故答案为:2.
【点睛】本题考查了数轴,相反数,根据这四个数中最小数与最大数的和等于10列出方程是解题的关键.
14.0
【分析】乘以任何数结果为.
【详解】解:,
故答案为:0.
【点睛】本题考查有理数的乘除法,是基础考点,掌握相关知识是解题关键.
15.
【分析】先凑100,然后根据乘法分配律进行计算即可求解.
【详解】解:,
故答案为:.
【点睛】本题考查了有理数的简便运算,凑整计算是解题的关键.
16.-1
【分析】根据有理数的除法运算可进行求解.
【详解】解:原式=;
故答案为-1.
【点睛】本题主要考查有理数的除法,熟练掌握有理数的除法运算是解题的关键.
17.见解析
【分析】根据正数、整数、分数的概念,即可得出答案.
【详解】正数集合:;
整数集合:;
分数集合:;
负整数集合:;
正分数集合:;
【点睛】本题考查了正数、整数、分数的概念,掌握以上内容是解题的关键.
18.(1)8
(2)3或9
【分析】(1)根据,可以求得a、b的值,从而可以求得点A、B表示的数;
(2)分两种情况:①当点P在线段上时;②当点P在线段延长线上时;分别 求解即可.
【详解】(1)解:∵,
∴,,
∴,,
即点A表示的数是,点B表示的数是5,
∴
(2)解:分两种情况:①点P在线段之间时,如图,
由 (1)知: ,
∵,,
∴,
∴,
∴点P在数轴上对应的数是3;
②点P在点B右侧时,如图,
由 (1)知: ,
∵,,
∴,
∴,
∴点P在数轴上对应的数是9.
综上所述:点P对应的数为3或9.
【点睛】本题考查数轴、非负数性质,线段和差倍分计算,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题,注意分类讨论思想的应用.
19.(1)见解析;(2);(3),,0.
【分析】(1)根据数轴的定义解答即可;
(2)根据数轴上的点表示的数右边的总比左边的大解答即可;
(3)根据绝对值的定义结合数轴解答即可.
【详解】解:(1)如图所示:
(2)由(1)可得:;
(3)由(1)可得,绝对值小于的所有整数有:,,0.
【点睛】本题考查了数轴、有理数比较大小,熟知数轴上的点表示的数右边的总比左边的大是解答本题的关键.
20.(1)
(2)①或,②或
【分析】(1)根据表示在数轴上数与数0对应点之间的距离,求解即可;
(2)①根据,表示在数轴上与3的距离为2的点对应的数,求出答案;
②根据,表示在数轴上表示数的点到表示数1与表示数3的距离之和为8,求出答案.
【详解】(1)解:,数轴上表示数的点到原点的距离为2,因此或,
故答案为:;
(2)①在数轴上到3的距离为2的点对应的数,
或.
②在数轴上到1和3的距离和为8的点对应的数,
或.
【点睛】本题考查了绝对值的几何意义,读懂并理解题目材料,会利用绝对值的几何意义是解决本题的关键.
21.(1)
(2)
(3)个
【分析】(1)根据正负数的意义,可知星期六产量最多,用即可求解.
(2)根据正负数的意义,可知星期二产量最少,用即可求解.
(3)用乘以再加上表格中的数据,即可求解.
【详解】(1)解:星期六产量最多,
故答案为:.
(2)解:星期二产量最少,
故答案为:.
(3)解:(个)
答:本周实际共生产个口罩.
【点睛】本题考查了正负数的意义,有理数的加减运算的应用,有理数的乘法的应用,根据题意列出算式是解题的关键.
22.(1)
(2)
(3)
【分析】(1)根据新定义运算的含义可得;
(2)根据新定义运算的含义可得;
(3)根据新定义运算的含义先列式,再裂项相消进行计算即可.
【详解】(1)解:;
(2);
(3)
.
【点睛】本题考查的是新定义运算,含乘方的有理数的混合运算,理解新定义运算的含义是解本题的关键.
23.(1)
(2)2
【分析】对于(1),先将小数变为分数,同时去括号,再根据有理数的加减法法则计算即可;
对于(2),先算乘方,同时计算括号内的,再计算乘除法,最后计算加减.
【详解】(1)原式
;
(2)原式
.
【点睛】本题主要考查了有理数的混合运算,掌握运算法则是解题的关键.即先算乘方,再算乘除,最后算加减,有括号的先计算括号内的.
24.(1)8
(2)
【分析】根据先乘方,再算乘除法,最后再算加减的有理数混合运算顺序进行计算即可.
【详解】(1)解:原式
;
(2)解:原式
.
【点睛】本题考查了含乘方的有理数的混合运算,熟练掌握有理数的混合运算顺序是计算本题的关键.
25.(1)见解析
(2)千米
(3)升
【分析】(1)根据具有相反意义的量即可得;
(2)将与表格中记作的四个数字相加即可得;
(3)根据上升和下降消耗燃油的情况列出运算式子,再根据有理数的乘法与加法法则进行计算即可得.
【详解】(1)解:因为上升和下降是一对具有相反意义的量,且上升千米记作,
所以完成表格如下:
高度变化 此刻高度记作
(2)解:
(千米),
答:飞机完成上述四个表演动作后,飞机高度是千米.
(3)解:
(升),
答:这架飞机在这4个动作表演过程中,一共消耗了33升燃油.
【点睛】本题主要考查了正负数在生活中的实际应用、有理数乘法与加减法的应用,正确列出运算式子是解题关键.
26.(1),答案不唯一
(2)见解析
【分析】(1)根据题意将其进行有理数的混合运算得到24即可;
(2)假设一组数字,再进行计算即可.
【详解】(1)由题意得:;
(2)由题意得,假设抽取的卡牌上的数字为:2、3、4、6,
则.(答案不唯一)
【点睛】本题考查了有理数的混合运算的应用,灵活运用所学知识求解是解决本题的关键.
一、单选题
1.(2023上·辽宁锦州·七年级统考期末)的相反数是( )
A. B. C. D.
2.(2023上·辽宁鞍山·七年级统考期末)某年我国人均水资源比上年的增幅是,后续三年各年比上年的增幅分别是,,,这些增幅中最小的是( )
A. B. C.13.0% D.
3.(2023上·辽宁锦州·七年级统考期末)我国是最早进行负数运算的国家,魏晋时期的数学家刘徽在其著作《九章算术注》中,用不同颜色的算筹《小棍形状的记数工具)分别表示正数和负数(白色为正,黑色为负),如图表示的是的计算过程,则图表示的计算过程是( )
A. B.
C. D.
4.(2023上·辽宁沈阳·七年级统考期末)如图是某市11月份连续四天的天气预报信息,其中日温差最大的一天是( )
11月11日 11月12日 11月13日 11月14日
多云 南风级 阵雨 北风级 阵雨 北风级 晴 西北风级
A.11月11日 B.11月12日 C.11月13日 D.11月14日
5.(2021上·辽宁盘锦·七年级统考期末)珠穆朗玛峰海拔高8848米,塔里木盆地海拔高—153米,求珠穆朗玛峰比塔里木盆地,高多少米列式正确的是( )
A.8848+153 B.8848+(-153)
C.8848-153 D.8848-(-153)
6.(2023上·辽宁锦州·七年级统考期末)如图,数轴上三点表示的有理数分别为,下列四个结论:①;②;③;④.其中正确结论的序号为( )
A.①②③ B.①②④ C.①③④ D.②③④
7.(2023上·辽宁葫芦岛·七年级统考期末)有理数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )
A. B. C. D.
8.(2023上·辽宁沈阳·七年级统考期末)下列说法正确的是( )
A.有理数的绝对值一定比0大
B.有理数的相反数一定比0小
C.如果两个数的绝对值相等,那么这两个数相等
D.乘积为1的两个数互为倒数
9.(2023上·辽宁辽阳·七年级统考期末)在,,,中,负数的个数是( )
A.4个 B.3个 C.2个 D.1个
10.(2023上·辽宁锦州·七年级统考期末)习近平总书记在中国共产党第二十次全国代表大会上的报告中指出:十年来,我国经济实力实现历史性跃升,国内生产总值从54万亿元增长到114万亿元,我国经济总量占世界经济的比重达18.5%,提高7.2个百分点,稳居世界第二位.数据114万亿用科学记数法表示为( )
A. B. C. D.
11.(2023上·辽宁葫芦岛·七年级统考期末)2022年我国新能源汽车保有量达辆,同比增长.请将用科学记数法表示为( )
A. B. C. D.
二、填空题
12.(2023上·辽宁葫芦岛·七年级统考期末)升降机在运行过程中,如果上升15米记作“+15米”,那么下降3米记作 米.
13.(2023上·辽宁沈阳·七年级统考期末)如图,数轴上点A,B,C,D表示的数分别为a,b,c,d,相邻两点间的距离均为2个单位长度.
(1)若a与c互为相反数,则 ;
(2)若这四个数中最小数与最大数的和等于10,则 .
14.(2023上·辽宁抚顺·七年级统考期末)计算:= .
15.(2023上·辽宁沈阳·七年级统考期末)计算: .
16.(2022·广西玉林·统考中考真题)计算: .
三、解答题
17.(2023上·辽宁沈阳·七年级统考期末)将下列各数填入所属的集合中:
0,,,,,3.5,0.6,,10,,,6.5
正数集合:{ …};
整数集合:{ …};
分数集合:{ …};
负整数集合:{ …};
正分数集合:{ …};
18.(2023上·辽宁抚顺·七年级统考期末)已知点A在数轴上的对应的数为a,点B对应的数为b,且满足.
(1)点A到点B的距离为_________;
(2)如图,点P是数轴上一点,点P到点A的距离是点P到点B的距离的3倍(即),求点P在数轴上对应的数.
19.(2023上·辽宁沈阳·七年级统考期末)(1)把6.5,,0,3,,表示在数轴上.
(2)请将上面的数用“<”连接起来;
(3)观察数轴,直接写出绝对值小于的所有整数.
20.(2023上·辽宁鞍山·七年级统考期末)阅读材料并回答问题:
的含义是数轴上表示数的点与原点的距离,即,也就是说,表示在数轴上数与数0对应的点之间的距离;因此可以推断表示在数轴上数与数1对应的点之间的距离.例如,,就是在数轴上到1的距离为2的点对应的数,即为或;回答问题:
(1)若,则的值是______;
(2)利用上述方法解下列方程:①;②
21.(2023上·辽宁抚顺·七年级统考期末)“新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩加工厂为满足市场需求,计划在本周每日生产个医用口罩,但是由于各种原因,实际每日生产量与计划每日生产量相比情况如下表(增加的口罩数为正数,减少的口罩数为负数):
星期 一 二 三 四 五 六 日
增减(单位:个)
(1)本周产量最多的一日生产了 个口罩;
(2)本周产量最少的一日生产了 个口罩;
(3)请你根据记录求出本周实际共生产多少个口罩?
22.(2023上·辽宁葫芦岛·七年级统考期末)式子“”表示从1开始的连续100个正整数的和,由于上述式子比较长,书写不方便,为了简便起见,可以将上述式子表示为,这里“”是求和的符号.例如“”用“”可以表示为;“.”用“”可以表示为.
(1)把写成加法的形式是______;
(2)“”用“”可以表示为______;
(3)计算:.
23.(2023上·辽宁辽阳·七年级统考期末)计算:
(1);
(2).
24.(2023上·辽宁朝阳·七年级统考期末)计算:
(1)
(2)
25.(2023上·辽宁抚顺·七年级统考期末)某空军举行特技飞行表演,其中一架飞机起飞0.5千米后的高度变化如下表:(“+”表示上升,“﹣”表示下降)
(1)完成表格;
高度变化 此刻高度记作
____
____
____
(2)飞机完成上述四个表演动作后,飞机高度是多少千米?
(3)如果飞机每上升1千米需消耗5升燃油,平均每下降1千米需消耗3升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
26.(2023上·辽宁鞍山·七年级统考期末)小明和同学们玩扑克牌游戏.游戏规则是:从一副扑克牌(去掉“大王”“小王”)中任意抽取四张,根据牌面上的数字进行混合运算,其中J代表11、Q代表12、K代表13,若每张牌上的数字只能用一次,并使得运算结果等于24.
(1)小明抽到的牌如图所示,请帮小明列出一个结果等于24的算式;
(2)请你抽取任意数字不相同的4张扑克牌,并列出一个结果等于24的算式.
参考答案:
1.D
【分析】只有符号不同的两个数叫做互为相反数,由此即可得到答案.
【详解】解:的相反数是.
故选:D.
【点睛】本题考查相反数,解题的关键是掌握相反数的定义.
2.D
【分析】根据有理数的大小得出结论即可.
【详解】解:,
故选:D.
【点睛】本题主要考查有理数大小的比较,熟练掌握有理数大小比较的方法是解题的关键.
3.A
【分析】通过观察图找到计算的过程与规律,类比图即可得出答案.
【详解】解:根据题意可知:一横表示,一竖表示,
通过观察,可知图和图的计算过程相同,只是数值的不同,
∴图中表示的计算过程是:,
故选:A.
【点睛】本题考查正数和负数,有理数的加法运算,解题关键能够类比题干中的信息从而解决问题.
4.C
【分析】分别求出每天的温差,然后进行比较即可.
【详解】解:11月11日温差为,
11月12日温差为,
11月13日温差为,
11月14日温差为,
∵,
∴日温差最大的一天是11月13日,故C正确.
故选:C.
【点睛】本题主要考查了有理数减法的应用,解题的关键是准确求出四天的温差.
5.D
【分析】直接用珠穆朗玛峰的海拔高度减去塔里木盆地的海拔高度即可表示.
【详解】,
故选:D.
【点睛】本题考查有理数减法的实际应用,理解用较大的数减去较小的数表示差值是解题关键.
6.B
【分析】根据即可判断①,根据即可判断②,根据,即可判断③,根据,即可判断④.
【详解】解:由题意可得,,
∴,故①正确;
∵,
∴,故②正确;
∵,,
∴,故③错误;
∵,,
∴,故④正确,
综上可知,正确结论是①②④,
故选:B
【点睛】此题考查了根据点在数轴上的位置判断式子的符号,熟练掌握有理数的运算法则是解题的关键.
7.C
【分析】由数轴可知,,,则,,据此逐一判断,即可得到答案.
【详解】解:由数轴可知,,,则,,
A、,原结论错误,不符合题意,选项错误;
B、,原结论错误,不符合题意,选项错误;
C、,原结论正确,符合题意,选项正确;
D、,原结论错误,不符合题意,选项错误;
故选:C.
【点睛】本题考查了数轴,有理数的加法、减法和乘法,熟练掌握数轴上点的特征是解题关键.
8.D
【分析】根据绝对值的非负性,相反数的定义,倒数的定义,逐一进行判断即可.
【详解】解:A、有理数的绝对值一定大于等于0,选项错误,不符合题意;
B、正有理数的相反数一定比0小,选项错误,不符合题意;
C、如果两个数的绝对值相等,那么这两个数相等或互为相反数,选项错误,不符合题意;
D、乘积为1的两个数互为倒数,选项正确,符合题意;
故选D.
【点睛】本题考查绝对值的意义,相反数和倒数.熟练掌握相关知识点,是解题的关键.
9.B
【分析】先将各数化简,然后根据负数的概念判断即可.
【详解】解:,,,
∴负数的个数是3.
故选B.
【点睛】本题主要考查多重符号的化简,乘方的运算以及绝对值的化简,熟练掌握计算方法是解决本题的关键.
10.C
【分析】科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正整数;当原数的绝对值时,n是负整数.
【详解】解:114万亿,
故选:C.
【点睛】本题主要考查科学记数法.科学记数法的表示形式为的形式,其中,n为整数.解题关键是正确确定a的值以及n的值.
11.C
【分析】用科学记数法表示较大的数时,一般形式为,其中,为整数,且比原来的整数位数少1,据此判断即可.
【详解】解:.
故选:C.
【点睛】本题考查了用科学记数法表示较大的数,一般形式为,其中,确定与的值是解本题的关键.
12.
【分析】根据升降机运行的过程中,如果上升米记作“米”,可以得到下降米应记作负数.
【详解】解:升降机运行的过程中,如果上升米记作“米”,那么下降3米应记作米.
故答案为:.
【点睛】本题考查了正数和负数的实际应用,掌握正数和负数的含义是解题的关键.
13. 4 2
【分析】(1)根据a与c互为相反数,知道点B是原点,根据相邻两点间的距离均为2个单位长度得到d的值;
(2)根据这四个数中最小数与最大数的和等于10,得到,由,得到一元一次方程,解方程即可得出答案.
【详解】(1)解:∵a与c互为相反数,
∴,,,,
故答案为:4;
(2)解:∵这四个数中最小数与最大数的和等于10,
∴,
∵相邻两点间的距离均为2个单位长度.
∴,即,
∴,
∴.
故答案为:2.
【点睛】本题考查了数轴,相反数,根据这四个数中最小数与最大数的和等于10列出方程是解题的关键.
14.0
【分析】乘以任何数结果为.
【详解】解:,
故答案为:0.
【点睛】本题考查有理数的乘除法,是基础考点,掌握相关知识是解题关键.
15.
【分析】先凑100,然后根据乘法分配律进行计算即可求解.
【详解】解:,
故答案为:.
【点睛】本题考查了有理数的简便运算,凑整计算是解题的关键.
16.-1
【分析】根据有理数的除法运算可进行求解.
【详解】解:原式=;
故答案为-1.
【点睛】本题主要考查有理数的除法,熟练掌握有理数的除法运算是解题的关键.
17.见解析
【分析】根据正数、整数、分数的概念,即可得出答案.
【详解】正数集合:;
整数集合:;
分数集合:;
负整数集合:;
正分数集合:;
【点睛】本题考查了正数、整数、分数的概念,掌握以上内容是解题的关键.
18.(1)8
(2)3或9
【分析】(1)根据,可以求得a、b的值,从而可以求得点A、B表示的数;
(2)分两种情况:①当点P在线段上时;②当点P在线段延长线上时;分别 求解即可.
【详解】(1)解:∵,
∴,,
∴,,
即点A表示的数是,点B表示的数是5,
∴
(2)解:分两种情况:①点P在线段之间时,如图,
由 (1)知: ,
∵,,
∴,
∴,
∴点P在数轴上对应的数是3;
②点P在点B右侧时,如图,
由 (1)知: ,
∵,,
∴,
∴,
∴点P在数轴上对应的数是9.
综上所述:点P对应的数为3或9.
【点睛】本题考查数轴、非负数性质,线段和差倍分计算,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题,注意分类讨论思想的应用.
19.(1)见解析;(2);(3),,0.
【分析】(1)根据数轴的定义解答即可;
(2)根据数轴上的点表示的数右边的总比左边的大解答即可;
(3)根据绝对值的定义结合数轴解答即可.
【详解】解:(1)如图所示:
(2)由(1)可得:;
(3)由(1)可得,绝对值小于的所有整数有:,,0.
【点睛】本题考查了数轴、有理数比较大小,熟知数轴上的点表示的数右边的总比左边的大是解答本题的关键.
20.(1)
(2)①或,②或
【分析】(1)根据表示在数轴上数与数0对应点之间的距离,求解即可;
(2)①根据,表示在数轴上与3的距离为2的点对应的数,求出答案;
②根据,表示在数轴上表示数的点到表示数1与表示数3的距离之和为8,求出答案.
【详解】(1)解:,数轴上表示数的点到原点的距离为2,因此或,
故答案为:;
(2)①在数轴上到3的距离为2的点对应的数,
或.
②在数轴上到1和3的距离和为8的点对应的数,
或.
【点睛】本题考查了绝对值的几何意义,读懂并理解题目材料,会利用绝对值的几何意义是解决本题的关键.
21.(1)
(2)
(3)个
【分析】(1)根据正负数的意义,可知星期六产量最多,用即可求解.
(2)根据正负数的意义,可知星期二产量最少,用即可求解.
(3)用乘以再加上表格中的数据,即可求解.
【详解】(1)解:星期六产量最多,
故答案为:.
(2)解:星期二产量最少,
故答案为:.
(3)解:(个)
答:本周实际共生产个口罩.
【点睛】本题考查了正负数的意义,有理数的加减运算的应用,有理数的乘法的应用,根据题意列出算式是解题的关键.
22.(1)
(2)
(3)
【分析】(1)根据新定义运算的含义可得;
(2)根据新定义运算的含义可得;
(3)根据新定义运算的含义先列式,再裂项相消进行计算即可.
【详解】(1)解:;
(2);
(3)
.
【点睛】本题考查的是新定义运算,含乘方的有理数的混合运算,理解新定义运算的含义是解本题的关键.
23.(1)
(2)2
【分析】对于(1),先将小数变为分数,同时去括号,再根据有理数的加减法法则计算即可;
对于(2),先算乘方,同时计算括号内的,再计算乘除法,最后计算加减.
【详解】(1)原式
;
(2)原式
.
【点睛】本题主要考查了有理数的混合运算,掌握运算法则是解题的关键.即先算乘方,再算乘除,最后算加减,有括号的先计算括号内的.
24.(1)8
(2)
【分析】根据先乘方,再算乘除法,最后再算加减的有理数混合运算顺序进行计算即可.
【详解】(1)解:原式
;
(2)解:原式
.
【点睛】本题考查了含乘方的有理数的混合运算,熟练掌握有理数的混合运算顺序是计算本题的关键.
25.(1)见解析
(2)千米
(3)升
【分析】(1)根据具有相反意义的量即可得;
(2)将与表格中记作的四个数字相加即可得;
(3)根据上升和下降消耗燃油的情况列出运算式子,再根据有理数的乘法与加法法则进行计算即可得.
【详解】(1)解:因为上升和下降是一对具有相反意义的量,且上升千米记作,
所以完成表格如下:
高度变化 此刻高度记作
(2)解:
(千米),
答:飞机完成上述四个表演动作后,飞机高度是千米.
(3)解:
(升),
答:这架飞机在这4个动作表演过程中,一共消耗了33升燃油.
【点睛】本题主要考查了正负数在生活中的实际应用、有理数乘法与加减法的应用,正确列出运算式子是解题关键.
26.(1),答案不唯一
(2)见解析
【分析】(1)根据题意将其进行有理数的混合运算得到24即可;
(2)假设一组数字,再进行计算即可.
【详解】(1)由题意得:;
(2)由题意得,假设抽取的卡牌上的数字为:2、3、4、6,
则.(答案不唯一)
【点睛】本题考查了有理数的混合运算的应用,灵活运用所学知识求解是解决本题的关键.
