人教版数学九年级上册 24.1.4 圆周角 学案(含答案)
文档属性
| 名称 | 人教版数学九年级上册 24.1.4 圆周角 学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 159.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 00:00:00 | ||
图片预览



文档简介
圆周角
班级:_____________姓名:__________________组号:_________
第二课时
一、旧知回顾
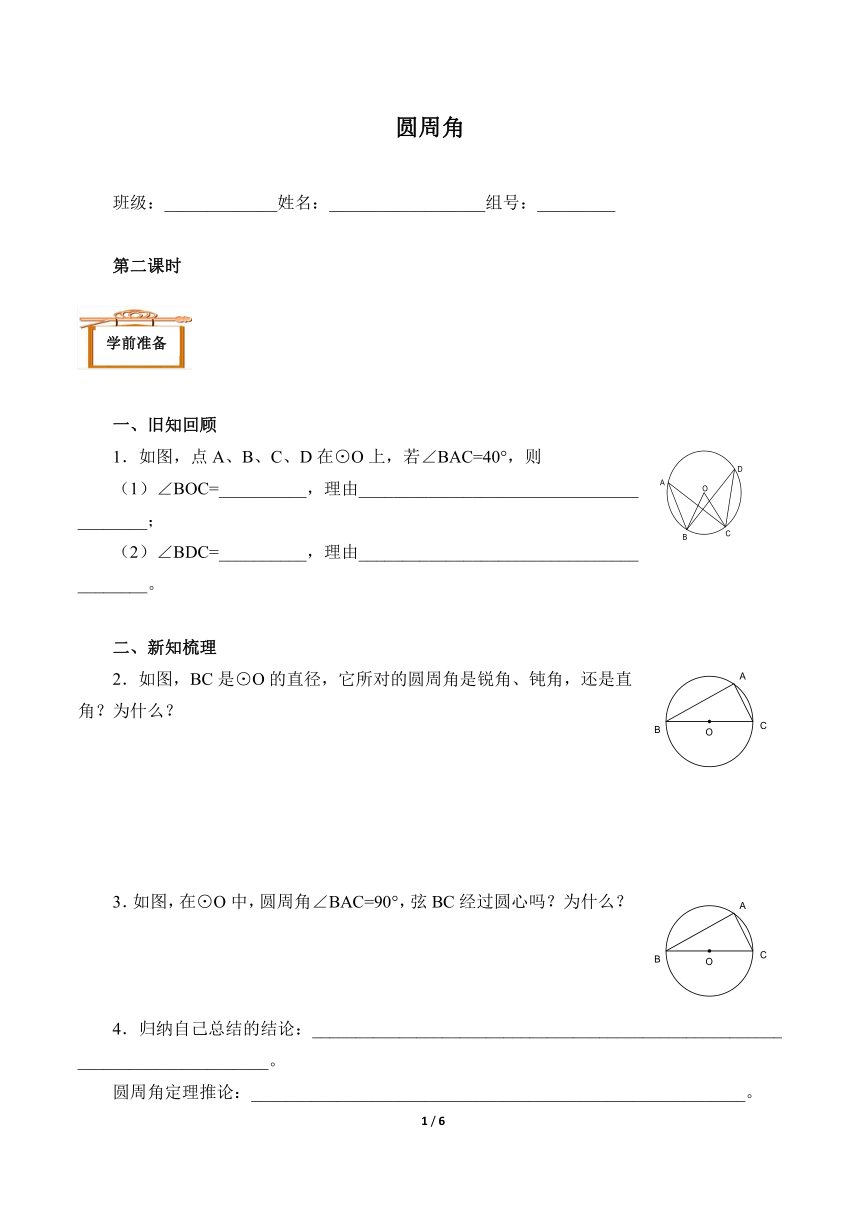
1.如图,点A、B、C、D在⊙O上,若∠BAC=40°,则
(1)∠BOC=__________,理由________________________________________;
(2)∠BDC=__________,理由________________________________________。
二、新知梳理
2.如图,BC是⊙O的直径,它所对的圆周角是锐角、钝角,还是直角?为什么?
3.如图,在⊙O中,圆周角∠BAC=90°,弦BC经过圆心吗?为什么?
4.归纳自己总结的结论:____________________________________________________________________________。
圆周角定理推论:_________________________________________________________。
注意:这里所对的角、90°的角必须是圆周角;
圆内接多边形的定义是什么?
_______________________________________________________________________________________________
5.如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。求证:∠A+∠C=180°。
三、试一试
6.如图,在⊙O中,△ABC是等边三角形,AD是直径,则∠ADB= ,∠DAB= 。
7.如图,AB是⊙O的直径,CD是弦,∠ACD=40°,则∠BCD=______,∠BOD=_ 。
★通过预习你还有什么困惑
一、课堂活动、记录
1.运用推理的方法说明推论的由来。
2.在应用推论时要注意什么?
3.圆内接四边形的四个角之间有什么关系?应用时应注意什么?
二、精练反馈
A组:
1.如图,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( )。
A.140° B.110° C.120° D.130°
2.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95
B组:
3.如图,AB是⊙O的直径,若AB=AC,求证:BD=CD。
三、课堂小结
1.圆周角的3个推论。
2.应用推论2时应注意什么?
3.圆内接四边形的对角互补的证明及应用。
四、拓展延伸(选做)
1.如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠CEB的度数。
2.如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E,AC=10,求AE的长。
【答案】
【学前准备】
旧知回顾
略
新知梳理
1.80°;同弧所对的圆周角等于它所对圆心角的一半;40°;同弧所对的圆周角相等
2.解:直角;∵∠BOC=180,∴∠BAC=∠BOC=
3.解:弦BC经过圆心,
∵∠BAC=90°,
∴∠BOC=2∠BAC=180°
∴弦BC经过圆心
4.直径所对的圆周角等于90°,90°的圆周角所对的弦为直径;如果一个多边形的所有顶点都在同一个圆上那么,这个多边形叫做圆的内接多边形
5.证明:连接OB、OD
∵弧BCD=弧BCD,
∴∠A=∠1,
∵弧BAD=弧BAD,∴∠BCD=∠2,
∵∠1+∠2=180°,∴∠A+∠C=180°
试一试
6.60°; 30°
7.50°; 100°
【课堂探究】
课堂活动、记录
略
精炼反馈
1.D
2.B
3.证明:连接AD
∵AB是⊙O的直径,
∴∠ADB=90°即,
∵AB=AC,∴BD=CD
课堂小结
略
拓展延伸(选做)
1.解:连接CB
∵AB是⊙O的直径
∴∠ACD+∠BCD=90°,
∵∠ACD=60°,∴∠BCD=30°
∵弧AC=弧AC,∴∠ABC=∠ADC=50°,
∵∠ECB+∠ABC+∠CEB=180°
∴∠CEB=100°
2.解:连接OE、OC
∵AO是⊙D的直径,
∴∠AEO=90°即OE⊥AC,
∵OA=OC,
∴AE=CE=AC=5
7 / 7
班级:_____________姓名:__________________组号:_________
第二课时
一、旧知回顾
1.如图,点A、B、C、D在⊙O上,若∠BAC=40°,则
(1)∠BOC=__________,理由________________________________________;
(2)∠BDC=__________,理由________________________________________。
二、新知梳理
2.如图,BC是⊙O的直径,它所对的圆周角是锐角、钝角,还是直角?为什么?
3.如图,在⊙O中,圆周角∠BAC=90°,弦BC经过圆心吗?为什么?
4.归纳自己总结的结论:____________________________________________________________________________。
圆周角定理推论:_________________________________________________________。
注意:这里所对的角、90°的角必须是圆周角;
圆内接多边形的定义是什么?
_______________________________________________________________________________________________
5.如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。求证:∠A+∠C=180°。
三、试一试
6.如图,在⊙O中,△ABC是等边三角形,AD是直径,则∠ADB= ,∠DAB= 。
7.如图,AB是⊙O的直径,CD是弦,∠ACD=40°,则∠BCD=______,∠BOD=_ 。
★通过预习你还有什么困惑
一、课堂活动、记录
1.运用推理的方法说明推论的由来。
2.在应用推论时要注意什么?
3.圆内接四边形的四个角之间有什么关系?应用时应注意什么?
二、精练反馈
A组:
1.如图,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( )。
A.140° B.110° C.120° D.130°
2.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95
B组:
3.如图,AB是⊙O的直径,若AB=AC,求证:BD=CD。
三、课堂小结
1.圆周角的3个推论。
2.应用推论2时应注意什么?
3.圆内接四边形的对角互补的证明及应用。
四、拓展延伸(选做)
1.如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠CEB的度数。
2.如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E,AC=10,求AE的长。
【答案】
【学前准备】
旧知回顾
略
新知梳理
1.80°;同弧所对的圆周角等于它所对圆心角的一半;40°;同弧所对的圆周角相等
2.解:直角;∵∠BOC=180,∴∠BAC=∠BOC=
3.解:弦BC经过圆心,
∵∠BAC=90°,
∴∠BOC=2∠BAC=180°
∴弦BC经过圆心
4.直径所对的圆周角等于90°,90°的圆周角所对的弦为直径;如果一个多边形的所有顶点都在同一个圆上那么,这个多边形叫做圆的内接多边形
5.证明:连接OB、OD
∵弧BCD=弧BCD,
∴∠A=∠1,
∵弧BAD=弧BAD,∴∠BCD=∠2,
∵∠1+∠2=180°,∴∠A+∠C=180°
试一试
6.60°; 30°
7.50°; 100°
【课堂探究】
课堂活动、记录
略
精炼反馈
1.D
2.B
3.证明:连接AD
∵AB是⊙O的直径,
∴∠ADB=90°即,
∵AB=AC,∴BD=CD
课堂小结
略
拓展延伸(选做)
1.解:连接CB
∵AB是⊙O的直径
∴∠ACD+∠BCD=90°,
∵∠ACD=60°,∴∠BCD=30°
∵弧AC=弧AC,∴∠ABC=∠ADC=50°,
∵∠ECB+∠ABC+∠CEB=180°
∴∠CEB=100°
2.解:连接OE、OC
∵AO是⊙D的直径,
∴∠AEO=90°即OE⊥AC,
∵OA=OC,
∴AE=CE=AC=5
7 / 7
同课章节目录
