人教版数学九年级上册第第二十四章 圆单元测试(含答案)
文档属性
| 名称 | 人教版数学九年级上册第第二十四章 圆单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 332.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 00:00:00 | ||
图片预览


文档简介
人教版数学9年级上册
第24单元测试
时间:120分钟 满分:120分
班级__________姓名__________得分__________
一、选择题(共12小题,满分36分,每小题3分)
1.(3分)(2022秋 邗江区校级月考)下列说法正确的是( )
A.同弧或等弧所对的圆心角相等
B.所对圆心角相等的弧是等弧
C.弧长相等的弧一定是等弧
D.平分弦的直径必垂直于弦
2.(3分)(2022秋 拱墅区月考)如图,四边形ABCD是⊙O的内接四边形,连接OA,OC.若∠ABC=108°,则∠AOC的度数为( )
A.72° B.108° C.144° D.150°
3.(3分)(2022秋 青秀区校级月考)如图,在Rt△ABC中,∠ACB=90°,⊙O与BC,AC分别相切于点E,F,BO平分∠ABC,连接OA.若BE=AC=6,⊙O的半径是2.则图中阴影部分的面积为( )
A.10π B.10 C.8﹣π D.6
4.(3分)(2022 鼓楼区校级模拟)如图,AD是⊙O的直径,PA,PB分别切⊙O于点A,B,若∠BCD=α,则∠P的度数是( )
A.90°﹣2α B.90°﹣α C.45° D.2α
5.(3分)(2022 汉阳区校级模拟)如图,将两个正方形如图放置(B,C,E共线,D,C,G共线),若AB=3,EF=2,点O在线段BC上,以OF为半径作⊙O,点A,点F都在⊙O上,则OD的长是( )
A.4 B. C. D.
6.(3分)(2022 巴中)如图,AB为⊙O的直径,弦CD交AB于点E,,∠CDB=30°,AC=2,则OE=( )
A. B. C.1 D.2
7.(3分)(2022 镇江)如图,在等腰△ABC中,∠BAC=120°,BC=6,⊙O同时与边BA的延长线、射线AC相切,⊙O的半径为3.将△ABC绕点A按顺时针方向旋转α(0°<α≤360°),B、C的对应点分别为B′、C′,在旋转的过程中边B′C′所在直线与⊙O相切的次数为( )
A.1 B.2 C.3 D.4
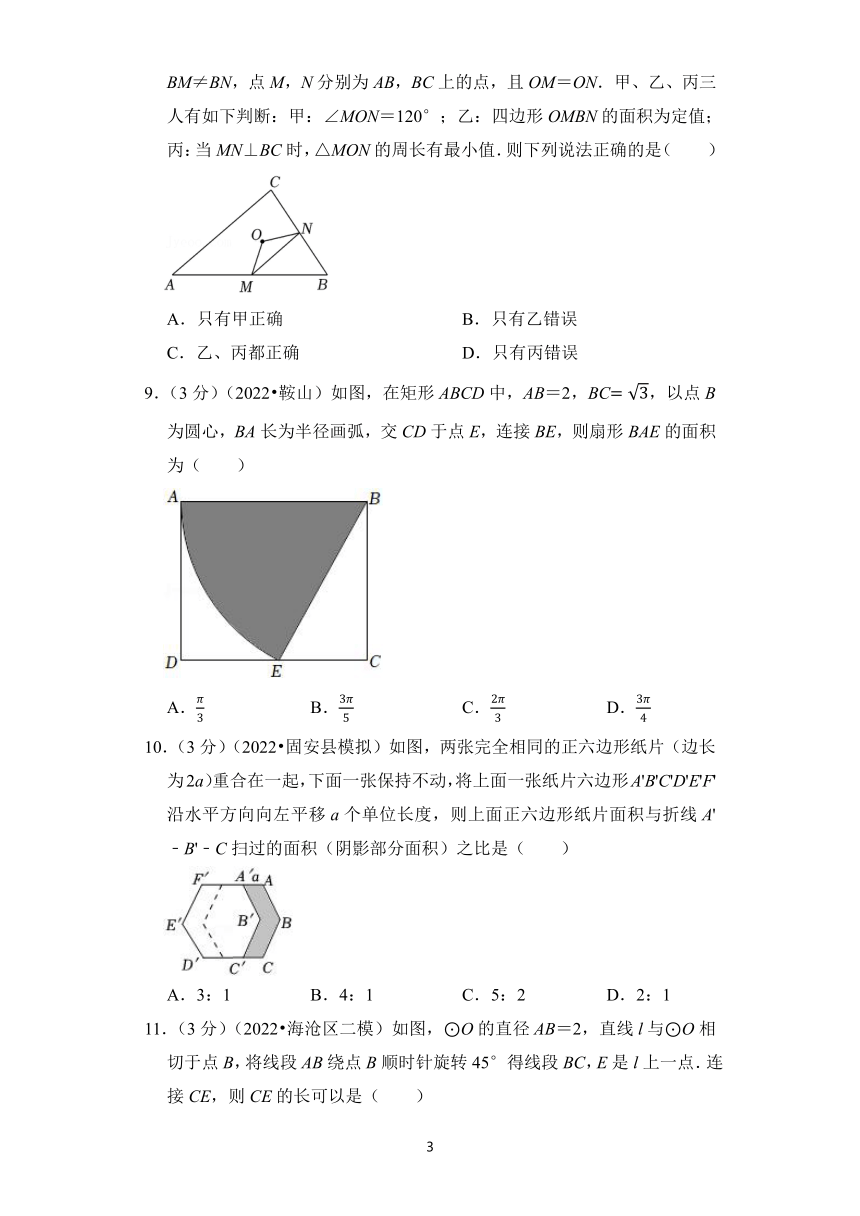
8.(3分)(2022 路南区三模)如图,点O为△ABC的内心,∠B=60°,BM≠BN,点M,N分别为AB,BC上的点,且OM=ON.甲、乙、丙三人有如下判断:甲:∠MON=120°;乙:四边形OMBN的面积为定值;丙:当MN⊥BC时,△MON的周长有最小值.则下列说法正确的是( )
A.只有甲正确 B.只有乙错误
C.乙、丙都正确 D.只有丙错误
9.(3分)(2022 鞍山)如图,在矩形ABCD中,AB=2,BC,以点B为圆心,BA长为半径画弧,交CD于点E,连接BE,则扇形BAE的面积为( )
A. B. C. D.
10.(3分)(2022 固安县模拟)如图,两张完全相同的正六边形纸片(边长为2a)重合在一起,下面一张保持不动,将上面一张纸片六边形A'B'C'D'E'F'沿水平方向向左平移a个单位长度,则上面正六边形纸片面积与折线A'﹣B'﹣C扫过的面积(阴影部分面积)之比是( )
A.3:1 B.4:1 C.5:2 D.2:1
11.(3分)(2022 海沧区二模)如图,⊙O的直径AB=2,直线l与⊙O相切于点B,将线段AB绕点B顺时针旋转45°得线段BC,E是l上一点.连接CE,则CE的长可以是( )
A.1 B.1.2 C.1.4 D.1.6
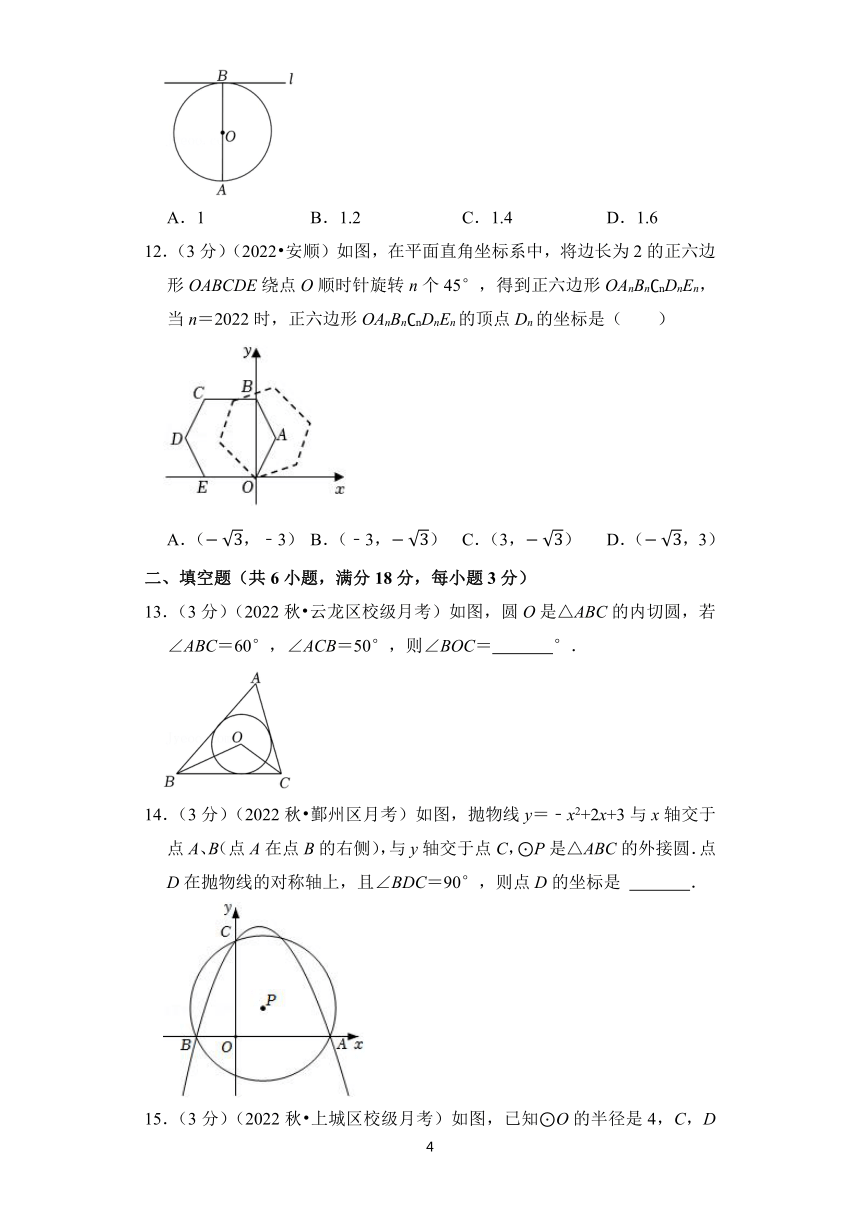
12.(3分)(2022 安顺)如图,在平面直角坐标系中,将边长为2的正六边形OABCDE绕点O顺时针旋转n个45°,得到正六边形OAnBn nDnEn,当n=2022时,正六边形OAnBn nDnEn的顶点Dn的坐标是( )
A.(,﹣3) B.(﹣3,) C.(3,) D.(,3)
二、填空题(共6小题,满分18分,每小题3分)
13.(3分)(2022秋 云龙区校级月考)如图,圆O是△ABC的内切圆,若∠ABC=60°,∠ACB=50°,则∠BOC= °.
14.(3分)(2022秋 鄞州区月考)如图,抛物线y=﹣x2+2x+3与x轴交于点A、B(点A在点B的右侧),与y轴交于点C,⊙P是△ABC的外接圆.点D在抛物线的对称轴上,且∠BDC=90°,则点D的坐标是 .
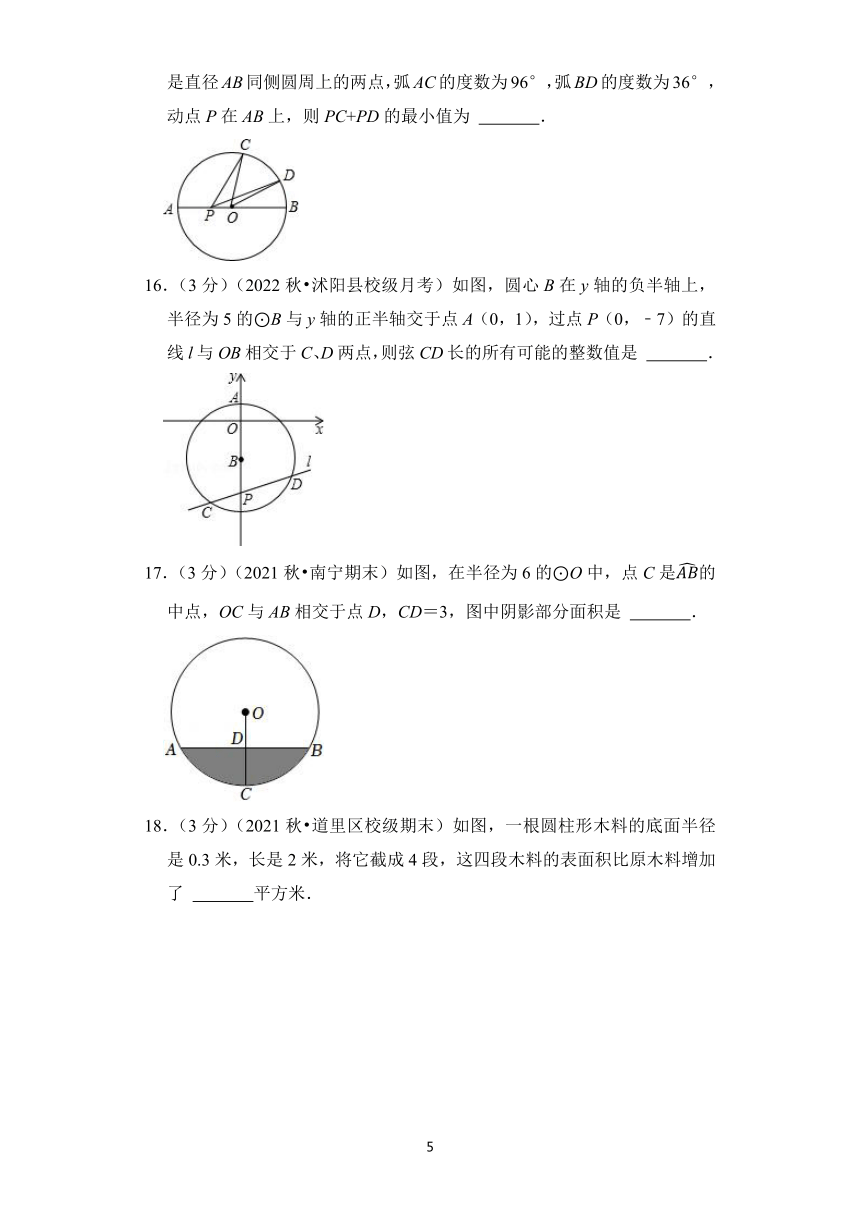
15.(3分)(2022秋 上城区校级月考)如图,已知⊙O的半径是4,C,D是直径AB同侧圆周上的两点,弧AC的度数为96°,弧BD的度数为36°,动点P在AB上,则PC+PD的最小值为 .
16.(3分)(2022秋 沭阳县校级月考)如图,圆心B在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与OB相交于C、D两点,则弦CD长的所有可能的整数值是 .
17.(3分)(2021秋 南宁期末)如图,在半径为6的⊙O中,点C是的中点,OC与AB相交于点D,CD=3,图中阴影部分面积是 .
18.(3分)(2021秋 道里区校级期末)如图,一根圆柱形木料的底面半径是0.3米,长是2米,将它截成4段,这四段木料的表面积比原木料增加了 平方米.
三、解答题(共7小题,满分66分)
19.(9分)(2022秋 滨江区校级月考)如图,已知AB是⊙O的直径,弦AC∥OD.
(1)求证:弧BD=弧CD;
(2)若的度数为58°,求∠AOD的度数.
20.(9分)(2022秋 泰州月考)如图,O是△ABC的外心,I是△ABC的内心,连接AI并延长交BC和⊙O于D,E.
(1)求证:EB=EI;
(2)若AB=8,AC=6,BE=4,求AI的长.
21.(9分)(2022秋 南京月考)如图,⊙O的弦AB、CD的延长线相交于点P,且PA=PC.求证:AB=CD.
22.(9分)(2022秋 仓山区校级月考)如图,将扇形AOB沿OB方向平移,使点O移到OB的中点O′处,得到扇形A′O′B′,若∠O=90°,OA=2,交O′A′于点C.
(1)连接OC,求∠AOC的度数;
(2)请直接写出阴影部分S阴影与S扇形AOC、S△OCO′的数量关系;并求出阴影部分的面积.
23.(10分)(2022 淮安)如图,△ABC是⊙O的内接三角形,∠ACB=60°,AD经过圆心O交⊙O于点E,连接BD,∠ADB=30°.
(1)判断直线BD与⊙O的位置关系,并说明理由;
(2)若AB=4,求图中阴影部分的面积.
24.(10分)(2021秋 乐清市期末)如图Rt△ABC中,∠ABC=90°,P是斜边AC上一个动点,以BP为直径作⊙O交BC于点D,与AC的另一个交点E,且,连接DE.
(1)若140°,求∠C的度数.
(2)求证AB=AP.
25.(10分)(2022 五华区校级模拟)如图,AB为⊙O直径,C,D为⊙O上的两点,且∠ACD=2∠A,CE⊥DB交DB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)若DE=2CE,AC=4,求⊙O的半径.
参考答案
一、选择题(共12小题,满分36分,每小题3分)
1.A
2.C
3.A
4.D
5.B
6.C
7.C
8.D
9.C
10.A
11.D
12.A;
二、填空题(共6小题,满分18分,每小题3分)
13.125
14.(1,1)或(1,2)
15.4
16.8,9,10
17.12π﹣9
18.1.6956;
三、解答题(共7小题,满分66分)
19.【解答】(1)证明:连接OC,
∵OC=OA,
∴∠C=∠A,
∵OD∥AC,
∴∠BOD=∠A,∠COD=∠C,
∴∠COD=∠BOD,
∴;
(2)解:∵的度数是58°,
∴∠AOC=58°,
∴∠BOC=180°﹣∠AOC=122°,
∵∠BOD=∠COD,
∴∠COD=∠BODBOC=61°,
∴∠AOD=∠AOC+∠COD=58°+61°=119°.
20.【解答】(1)证明:∵I是△ABC的内心,
∴AE平分∠CAB,BI平分∠ABC,
∴∠BAE=∠CAE,∠ABI=∠CBI,
∵∠BIE=∠BAE+∠ABI,∠IBE=∠IBD+∠EBD,
∵∠CBE=∠CAE,
∴∠BIE=∠EBI,
∴EB=EI;
(2)解:连接EC.
∵∠BAE=∠CAE,
∴,
∴BE=EC=4,
∵∠ADB=∠CDE,∠BAD=∠DCE,
∴△ADB∽△CDE,
∴2,设DE=m,CD=n,则BD=2m,AD=2n,
同法可证:△ADC∽△BDE,
∴,
∴,
∴n:m=3:2,设n=3k,m=2k,
∵∠CED=∠AEC,∠ECD=∠BAE=∠CAE,
∴△ECD∽△EAC,
∴EC2=ED EA,
∴8=m (m+2n),
∴8=2k(2k+6k)
∴k=1或﹣1(舍弃),
∴DE=2,AD=6,
∴AE=8,
∵EI=BE=4,
∴AI=AE﹣EI=4.
21.【解答】证明:连接AC,
∵PA=PC,
∴∠A=∠C,
∴,
∴,
∴,
∴AB=CD.
22.【解答】解:(1)如图,∵OC=OB,OO′=O′B,
∴OC=2OO′,
∵∠OO′C=90°,
∴∠O′CO=30°,∠COO′=60°,
∵∠AOB=90°,
∴∠AOC=90°﹣60°=30°;
(2)S阴=S扇形O′A′B′﹣(S扇形OCB﹣S△OCO′)
=S扇形AOB﹣S扇形OCB+S△OCO′
=S扇形AOC+S△OCO′.
∴S阴1.
23.【解答】解:(1)直线BD与⊙O相切,
理由:连接BE,
∵∠ACB=60°,
∴∠AEB=∠C=60°,
连接OB,
∵OB=OC,
∴△OBE是等边三角形,
∴∠BOD=60°,
∵∠ADB=30°,
∴∠OBD=180°﹣60°﹣30°=90°,
∴OB⊥BD,
∵OB是⊙O的半径,
∴直线BD与⊙O相切;
(2)∵AE是⊙O的直径,
∴∠ABE=90°,
∵AB=4,
∴sin∠AEB=sin60°,
∴AE=8,
∴OB=4,
∴BDOB=4,
∴图中阴影部分的面积=S△OBD﹣S扇形BOE48.
24.【解答】(1)解:连接BE,如图,
∵BP是直径,
∴∠BEC=90°,
∵140°,
∴40°,
∵,
∴80°,
∴∠CBE=40°,
∴∠C=50°;
②证明:∵,
∴∠CBP=∠EBP,
∵∠ABE+∠A=90°,∠C+∠A=90°,
∴∠C=∠ABE,
∵∠APB=∠CBP+∠C,∠ABP=∠EBP+∠ABE,
∴∠APB=∠ABP,
∴AP=AB.
25.【解答】(1)证明:连接OC,
∵CE⊥DE,
∴∠E=90°,
∵OA=OC,
∴∠A=∠ACO,
∵∠ACD=2∠A,
∴∠ACD=2∠ACO,
∴∠ACO=∠DCO,
∴∠A=∠DCO,
∵∠A=∠D,
∴∠D=∠DCO,
∴OC∥DE,
∴∠E+∠OCE=180°,
∴∠OCE=90°,
∵OC是⊙O的半径,
∴直线CE与⊙O相切;
(2)解:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠OCB=90°,
∵∠OCB+∠BCE=∠OCE=90°,
∴∠ACO=∠BCE,
∵∠D=∠A=∠ACO,
∴∠D=∠BCE,
又∠BEC=∠CED=90°,
∴△BCE∽△CDE,
∵2,
∴BCCE,
∵OC=OB,
∴∠OCB=∠OBC,
∵OC∥ED,
∴∠OCB=∠CBE,
∴∠CBE=∠OBC,
∵∠E=∠ACB=90°,
∴△BEC∽△BCA,
∴,
∴,
∵AC=4,
∴AB=2,
∴OA,
即⊙O的半径为.
2
第24单元测试
时间:120分钟 满分:120分
班级__________姓名__________得分__________
一、选择题(共12小题,满分36分,每小题3分)
1.(3分)(2022秋 邗江区校级月考)下列说法正确的是( )
A.同弧或等弧所对的圆心角相等
B.所对圆心角相等的弧是等弧
C.弧长相等的弧一定是等弧
D.平分弦的直径必垂直于弦
2.(3分)(2022秋 拱墅区月考)如图,四边形ABCD是⊙O的内接四边形,连接OA,OC.若∠ABC=108°,则∠AOC的度数为( )
A.72° B.108° C.144° D.150°
3.(3分)(2022秋 青秀区校级月考)如图,在Rt△ABC中,∠ACB=90°,⊙O与BC,AC分别相切于点E,F,BO平分∠ABC,连接OA.若BE=AC=6,⊙O的半径是2.则图中阴影部分的面积为( )
A.10π B.10 C.8﹣π D.6
4.(3分)(2022 鼓楼区校级模拟)如图,AD是⊙O的直径,PA,PB分别切⊙O于点A,B,若∠BCD=α,则∠P的度数是( )
A.90°﹣2α B.90°﹣α C.45° D.2α
5.(3分)(2022 汉阳区校级模拟)如图,将两个正方形如图放置(B,C,E共线,D,C,G共线),若AB=3,EF=2,点O在线段BC上,以OF为半径作⊙O,点A,点F都在⊙O上,则OD的长是( )
A.4 B. C. D.
6.(3分)(2022 巴中)如图,AB为⊙O的直径,弦CD交AB于点E,,∠CDB=30°,AC=2,则OE=( )
A. B. C.1 D.2
7.(3分)(2022 镇江)如图,在等腰△ABC中,∠BAC=120°,BC=6,⊙O同时与边BA的延长线、射线AC相切,⊙O的半径为3.将△ABC绕点A按顺时针方向旋转α(0°<α≤360°),B、C的对应点分别为B′、C′,在旋转的过程中边B′C′所在直线与⊙O相切的次数为( )
A.1 B.2 C.3 D.4
8.(3分)(2022 路南区三模)如图,点O为△ABC的内心,∠B=60°,BM≠BN,点M,N分别为AB,BC上的点,且OM=ON.甲、乙、丙三人有如下判断:甲:∠MON=120°;乙:四边形OMBN的面积为定值;丙:当MN⊥BC时,△MON的周长有最小值.则下列说法正确的是( )
A.只有甲正确 B.只有乙错误
C.乙、丙都正确 D.只有丙错误
9.(3分)(2022 鞍山)如图,在矩形ABCD中,AB=2,BC,以点B为圆心,BA长为半径画弧,交CD于点E,连接BE,则扇形BAE的面积为( )
A. B. C. D.
10.(3分)(2022 固安县模拟)如图,两张完全相同的正六边形纸片(边长为2a)重合在一起,下面一张保持不动,将上面一张纸片六边形A'B'C'D'E'F'沿水平方向向左平移a个单位长度,则上面正六边形纸片面积与折线A'﹣B'﹣C扫过的面积(阴影部分面积)之比是( )
A.3:1 B.4:1 C.5:2 D.2:1
11.(3分)(2022 海沧区二模)如图,⊙O的直径AB=2,直线l与⊙O相切于点B,将线段AB绕点B顺时针旋转45°得线段BC,E是l上一点.连接CE,则CE的长可以是( )
A.1 B.1.2 C.1.4 D.1.6
12.(3分)(2022 安顺)如图,在平面直角坐标系中,将边长为2的正六边形OABCDE绕点O顺时针旋转n个45°,得到正六边形OAnBn nDnEn,当n=2022时,正六边形OAnBn nDnEn的顶点Dn的坐标是( )
A.(,﹣3) B.(﹣3,) C.(3,) D.(,3)
二、填空题(共6小题,满分18分,每小题3分)
13.(3分)(2022秋 云龙区校级月考)如图,圆O是△ABC的内切圆,若∠ABC=60°,∠ACB=50°,则∠BOC= °.
14.(3分)(2022秋 鄞州区月考)如图,抛物线y=﹣x2+2x+3与x轴交于点A、B(点A在点B的右侧),与y轴交于点C,⊙P是△ABC的外接圆.点D在抛物线的对称轴上,且∠BDC=90°,则点D的坐标是 .
15.(3分)(2022秋 上城区校级月考)如图,已知⊙O的半径是4,C,D是直径AB同侧圆周上的两点,弧AC的度数为96°,弧BD的度数为36°,动点P在AB上,则PC+PD的最小值为 .
16.(3分)(2022秋 沭阳县校级月考)如图,圆心B在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与OB相交于C、D两点,则弦CD长的所有可能的整数值是 .
17.(3分)(2021秋 南宁期末)如图,在半径为6的⊙O中,点C是的中点,OC与AB相交于点D,CD=3,图中阴影部分面积是 .
18.(3分)(2021秋 道里区校级期末)如图,一根圆柱形木料的底面半径是0.3米,长是2米,将它截成4段,这四段木料的表面积比原木料增加了 平方米.
三、解答题(共7小题,满分66分)
19.(9分)(2022秋 滨江区校级月考)如图,已知AB是⊙O的直径,弦AC∥OD.
(1)求证:弧BD=弧CD;
(2)若的度数为58°,求∠AOD的度数.
20.(9分)(2022秋 泰州月考)如图,O是△ABC的外心,I是△ABC的内心,连接AI并延长交BC和⊙O于D,E.
(1)求证:EB=EI;
(2)若AB=8,AC=6,BE=4,求AI的长.
21.(9分)(2022秋 南京月考)如图,⊙O的弦AB、CD的延长线相交于点P,且PA=PC.求证:AB=CD.
22.(9分)(2022秋 仓山区校级月考)如图,将扇形AOB沿OB方向平移,使点O移到OB的中点O′处,得到扇形A′O′B′,若∠O=90°,OA=2,交O′A′于点C.
(1)连接OC,求∠AOC的度数;
(2)请直接写出阴影部分S阴影与S扇形AOC、S△OCO′的数量关系;并求出阴影部分的面积.
23.(10分)(2022 淮安)如图,△ABC是⊙O的内接三角形,∠ACB=60°,AD经过圆心O交⊙O于点E,连接BD,∠ADB=30°.
(1)判断直线BD与⊙O的位置关系,并说明理由;
(2)若AB=4,求图中阴影部分的面积.
24.(10分)(2021秋 乐清市期末)如图Rt△ABC中,∠ABC=90°,P是斜边AC上一个动点,以BP为直径作⊙O交BC于点D,与AC的另一个交点E,且,连接DE.
(1)若140°,求∠C的度数.
(2)求证AB=AP.
25.(10分)(2022 五华区校级模拟)如图,AB为⊙O直径,C,D为⊙O上的两点,且∠ACD=2∠A,CE⊥DB交DB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)若DE=2CE,AC=4,求⊙O的半径.
参考答案
一、选择题(共12小题,满分36分,每小题3分)
1.A
2.C
3.A
4.D
5.B
6.C
7.C
8.D
9.C
10.A
11.D
12.A;
二、填空题(共6小题,满分18分,每小题3分)
13.125
14.(1,1)或(1,2)
15.4
16.8,9,10
17.12π﹣9
18.1.6956;
三、解答题(共7小题,满分66分)
19.【解答】(1)证明:连接OC,
∵OC=OA,
∴∠C=∠A,
∵OD∥AC,
∴∠BOD=∠A,∠COD=∠C,
∴∠COD=∠BOD,
∴;
(2)解:∵的度数是58°,
∴∠AOC=58°,
∴∠BOC=180°﹣∠AOC=122°,
∵∠BOD=∠COD,
∴∠COD=∠BODBOC=61°,
∴∠AOD=∠AOC+∠COD=58°+61°=119°.
20.【解答】(1)证明:∵I是△ABC的内心,
∴AE平分∠CAB,BI平分∠ABC,
∴∠BAE=∠CAE,∠ABI=∠CBI,
∵∠BIE=∠BAE+∠ABI,∠IBE=∠IBD+∠EBD,
∵∠CBE=∠CAE,
∴∠BIE=∠EBI,
∴EB=EI;
(2)解:连接EC.
∵∠BAE=∠CAE,
∴,
∴BE=EC=4,
∵∠ADB=∠CDE,∠BAD=∠DCE,
∴△ADB∽△CDE,
∴2,设DE=m,CD=n,则BD=2m,AD=2n,
同法可证:△ADC∽△BDE,
∴,
∴,
∴n:m=3:2,设n=3k,m=2k,
∵∠CED=∠AEC,∠ECD=∠BAE=∠CAE,
∴△ECD∽△EAC,
∴EC2=ED EA,
∴8=m (m+2n),
∴8=2k(2k+6k)
∴k=1或﹣1(舍弃),
∴DE=2,AD=6,
∴AE=8,
∵EI=BE=4,
∴AI=AE﹣EI=4.
21.【解答】证明:连接AC,
∵PA=PC,
∴∠A=∠C,
∴,
∴,
∴,
∴AB=CD.
22.【解答】解:(1)如图,∵OC=OB,OO′=O′B,
∴OC=2OO′,
∵∠OO′C=90°,
∴∠O′CO=30°,∠COO′=60°,
∵∠AOB=90°,
∴∠AOC=90°﹣60°=30°;
(2)S阴=S扇形O′A′B′﹣(S扇形OCB﹣S△OCO′)
=S扇形AOB﹣S扇形OCB+S△OCO′
=S扇形AOC+S△OCO′.
∴S阴1.
23.【解答】解:(1)直线BD与⊙O相切,
理由:连接BE,
∵∠ACB=60°,
∴∠AEB=∠C=60°,
连接OB,
∵OB=OC,
∴△OBE是等边三角形,
∴∠BOD=60°,
∵∠ADB=30°,
∴∠OBD=180°﹣60°﹣30°=90°,
∴OB⊥BD,
∵OB是⊙O的半径,
∴直线BD与⊙O相切;
(2)∵AE是⊙O的直径,
∴∠ABE=90°,
∵AB=4,
∴sin∠AEB=sin60°,
∴AE=8,
∴OB=4,
∴BDOB=4,
∴图中阴影部分的面积=S△OBD﹣S扇形BOE48.
24.【解答】(1)解:连接BE,如图,
∵BP是直径,
∴∠BEC=90°,
∵140°,
∴40°,
∵,
∴80°,
∴∠CBE=40°,
∴∠C=50°;
②证明:∵,
∴∠CBP=∠EBP,
∵∠ABE+∠A=90°,∠C+∠A=90°,
∴∠C=∠ABE,
∵∠APB=∠CBP+∠C,∠ABP=∠EBP+∠ABE,
∴∠APB=∠ABP,
∴AP=AB.
25.【解答】(1)证明:连接OC,
∵CE⊥DE,
∴∠E=90°,
∵OA=OC,
∴∠A=∠ACO,
∵∠ACD=2∠A,
∴∠ACD=2∠ACO,
∴∠ACO=∠DCO,
∴∠A=∠DCO,
∵∠A=∠D,
∴∠D=∠DCO,
∴OC∥DE,
∴∠E+∠OCE=180°,
∴∠OCE=90°,
∵OC是⊙O的半径,
∴直线CE与⊙O相切;
(2)解:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠OCB=90°,
∵∠OCB+∠BCE=∠OCE=90°,
∴∠ACO=∠BCE,
∵∠D=∠A=∠ACO,
∴∠D=∠BCE,
又∠BEC=∠CED=90°,
∴△BCE∽△CDE,
∵2,
∴BCCE,
∵OC=OB,
∴∠OCB=∠OBC,
∵OC∥ED,
∴∠OCB=∠CBE,
∴∠CBE=∠OBC,
∵∠E=∠ACB=90°,
∴△BEC∽△BCA,
∴,
∴,
∵AC=4,
∴AB=2,
∴OA,
即⊙O的半径为.
2
同课章节目录
