11.6 轴对称 课件(共22张PPT)
文档属性
| 名称 | 11.6 轴对称 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 20:38:29 | ||
图片预览







文档简介
(共22张PPT)
第十一章 图形的运动
第3节 图形的翻折
11.6 轴对称
1.理解两个图形关于一条直线成轴对称的意义,知道轴对称的基本性质
2.掌握“轴对称图形”与“两个图形关于一条直线成轴对称”这两个概念的区别与联系
3.会用轴对称的有关性质画出已知图形关于某一条直线对称的图形
4.能画出成轴对称的两个图形的对称轴
下列图形,你能发现什么共同的特征
观察1
如图11-25,左、右两个图形中,左边的图形沿直线l翻折后.可以与右边的图形重合
l
观察中的图形都有这个特征:
如果把一个图形沿某一条直线翻折,能与另一个图形重合,那么叫做这两个图形关于这条直线成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做关于这条直线的对称点.
(1)图形的翻折变换就是轴对称变换
(2)对称轴是一条直线,而不是射线或线段
(3)轴对称是图形变换的一种方式.
注意
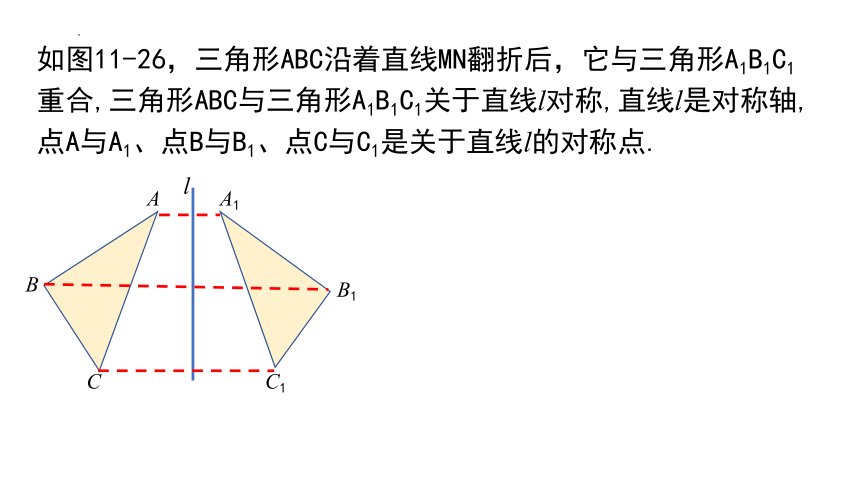
如图11-26,三角形ABC沿着直线MN翻折后,它与三角形A1B1C1重合,三角形ABC与三角形A1B1C1关于直线l对称,直线l是对称轴,点A与A1、点B与B1、点C与C1是关于直线l的对称点.
l
A
B
C
A1
B1
C1
两个图形关于一条直线成轴对称,这两个图形对应线段的长度相等,对应角的大小相等,它们的形状相同,大小不变.
两个图形关于一条直线成轴对称,对称点的联结线段被对称轴垂直平分;如果对应线段(或其延长线)相交,那么它们的交点在对称轴上.
轴对称的性质
例题1 如何画一个点的轴对称图形?
如图,画出点 A 关于直线 l 的对称点 A′.
·
l
A
·
A′
O
作法:
(1) 过点 A 作 l 的垂线,垂足为点 O;
(2) 在垂线上截取 OA′=OA.
点 A′ 就是点 A 关于直线 l 的对称点.
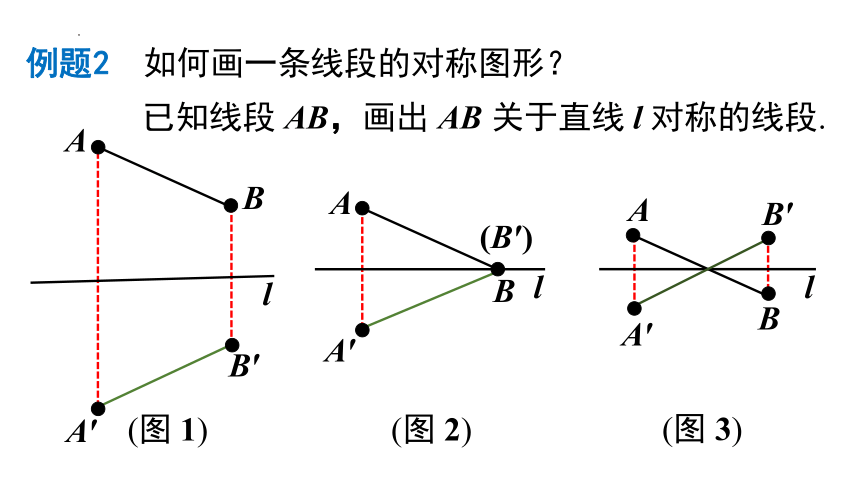
例题2 如何画一条线段的对称图形?
已知线段 AB,画出 AB 关于直线 l 对称的线段.
A
B
(图 1)
(图 2)
(图 3)
l
A
B
l
A′
A′
A′
B′
(B′)
B′
A
B
l
例题3 如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
A
B
C
分析:△ABC 可以由三个
顶点的位置确定,只要分
别画出这三个顶点关于直
线 l 的对称点,顺次连接
这些对称点,就能得到要
画的图形.
作法:(1) 过点 A 画直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,A′ 就是点 A 关于直线 l 的对称点.
(3) 连接 A′B′,B′C′,C′A′,得到的
△A′B′C′ 即为所求.
(2) 同理,分别画出点 B,C 关于直线 l 的对称点 B′,C′.
A
B
C
A′
B′
C′
O
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段的端点,三角形、四边形的顶点等)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
方法归纳
作轴对称图形的方法
例题4 在 3×3 的正方形格点图中,有格点△ABC 和△DEF,且△ABC 和△DEF 关于某直线成轴对称,
请在下面给出的图中画出 4 个这样的△DEF.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
1.如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到( )
A.三角形 B.梯形 C.正方形 D.五边形
C
2.如图,△AOD关于直线l进行轴对称变换后得到△BOC,则以下结论中不正确的是( )
A.∠1=∠2
B.∠3=∠4
C.l垂直平分AB,且l垂直平分CD
D.AC与BD互相平分
D
3.七巧板是我国的一种传统智力玩具,下列用七巧板拼成的图形是轴对称图形的是( )
D
4.下面是四名同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
B
5.如图,正三角形网格中,已有两个小三角形被涂黑.
(1)再将图①中其余小三角形涂黑一个,使整个被涂黑
的图案构成一个轴对称图形(画出两种不同的);
解:如图①所示.(答案不唯一)
(2)再将图②中其余小三角形涂黑两个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的).
解:如图②所示.(答案不唯一)
6. 如图,在 2×2 的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC 成轴对称且以格点为顶点的三角形,这样的三角形共有____个. 请在下面所给的格纸中一一画出 (所给的六个格纸未必全用).
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
5
1.(概念)如果把一个图形沿某一条直线翻折,能与另一个图形重合,那么叫做这两个图形关于这条直线成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做关于这条直线的对称点.
2.(性质)这两个图形对应线段的长度相等,对应角的大小相等,它们的形状相同,大小不变.两个图形关于一条直线成轴对称,对称点的联结线段被对称轴垂直平分;如果对应线段(或其延长线)相交,那么它们的交点在对称轴上.
3.(作图)几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段的端点,三角形、四边形的顶点等)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
第十一章 图形的运动
第3节 图形的翻折
11.6 轴对称
1.理解两个图形关于一条直线成轴对称的意义,知道轴对称的基本性质
2.掌握“轴对称图形”与“两个图形关于一条直线成轴对称”这两个概念的区别与联系
3.会用轴对称的有关性质画出已知图形关于某一条直线对称的图形
4.能画出成轴对称的两个图形的对称轴
下列图形,你能发现什么共同的特征
观察1
如图11-25,左、右两个图形中,左边的图形沿直线l翻折后.可以与右边的图形重合
l
观察中的图形都有这个特征:
如果把一个图形沿某一条直线翻折,能与另一个图形重合,那么叫做这两个图形关于这条直线成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做关于这条直线的对称点.
(1)图形的翻折变换就是轴对称变换
(2)对称轴是一条直线,而不是射线或线段
(3)轴对称是图形变换的一种方式.
注意
如图11-26,三角形ABC沿着直线MN翻折后,它与三角形A1B1C1重合,三角形ABC与三角形A1B1C1关于直线l对称,直线l是对称轴,点A与A1、点B与B1、点C与C1是关于直线l的对称点.
l
A
B
C
A1
B1
C1
两个图形关于一条直线成轴对称,这两个图形对应线段的长度相等,对应角的大小相等,它们的形状相同,大小不变.
两个图形关于一条直线成轴对称,对称点的联结线段被对称轴垂直平分;如果对应线段(或其延长线)相交,那么它们的交点在对称轴上.
轴对称的性质
例题1 如何画一个点的轴对称图形?
如图,画出点 A 关于直线 l 的对称点 A′.
·
l
A
·
A′
O
作法:
(1) 过点 A 作 l 的垂线,垂足为点 O;
(2) 在垂线上截取 OA′=OA.
点 A′ 就是点 A 关于直线 l 的对称点.
例题2 如何画一条线段的对称图形?
已知线段 AB,画出 AB 关于直线 l 对称的线段.
A
B
(图 1)
(图 2)
(图 3)
l
A
B
l
A′
A′
A′
B′
(B′)
B′
A
B
l
例题3 如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
A
B
C
分析:△ABC 可以由三个
顶点的位置确定,只要分
别画出这三个顶点关于直
线 l 的对称点,顺次连接
这些对称点,就能得到要
画的图形.
作法:(1) 过点 A 画直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,A′ 就是点 A 关于直线 l 的对称点.
(3) 连接 A′B′,B′C′,C′A′,得到的
△A′B′C′ 即为所求.
(2) 同理,分别画出点 B,C 关于直线 l 的对称点 B′,C′.
A
B
C
A′
B′
C′
O
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段的端点,三角形、四边形的顶点等)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
方法归纳
作轴对称图形的方法
例题4 在 3×3 的正方形格点图中,有格点△ABC 和△DEF,且△ABC 和△DEF 关于某直线成轴对称,
请在下面给出的图中画出 4 个这样的△DEF.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
1.如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到( )
A.三角形 B.梯形 C.正方形 D.五边形
C
2.如图,△AOD关于直线l进行轴对称变换后得到△BOC,则以下结论中不正确的是( )
A.∠1=∠2
B.∠3=∠4
C.l垂直平分AB,且l垂直平分CD
D.AC与BD互相平分
D
3.七巧板是我国的一种传统智力玩具,下列用七巧板拼成的图形是轴对称图形的是( )
D
4.下面是四名同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
B
5.如图,正三角形网格中,已有两个小三角形被涂黑.
(1)再将图①中其余小三角形涂黑一个,使整个被涂黑
的图案构成一个轴对称图形(画出两种不同的);
解:如图①所示.(答案不唯一)
(2)再将图②中其余小三角形涂黑两个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的).
解:如图②所示.(答案不唯一)
6. 如图,在 2×2 的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC 成轴对称且以格点为顶点的三角形,这样的三角形共有____个. 请在下面所给的格纸中一一画出 (所给的六个格纸未必全用).
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
5
1.(概念)如果把一个图形沿某一条直线翻折,能与另一个图形重合,那么叫做这两个图形关于这条直线成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做关于这条直线的对称点.
2.(性质)这两个图形对应线段的长度相等,对应角的大小相等,它们的形状相同,大小不变.两个图形关于一条直线成轴对称,对称点的联结线段被对称轴垂直平分;如果对应线段(或其延长线)相交,那么它们的交点在对称轴上.
3.(作图)几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段的端点,三角形、四边形的顶点等)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
