1.5 三角形函数的应用 课件(共21张PPT)
文档属性
| 名称 | 1.5 三角形函数的应用 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 26.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第一章 直角三角形的边角关系
第5节 三角函数的应用
学习目标
1.正确理解方位角、仰角和坡角的概念;(重点)
2.能运用解直角三角形知识解决方位角、仰角和坡角的问题.(难点)
情景引入
1.解直角三角形的意义:在直角三角形中,由已知元素求出所有未知元素的过程,叫做直角三角形.
2.直角三角形中诸元素之间的关系:
(1)三边之间的关系:a2+b2=c2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
把∠A换成∠B同样适用.
我们已经知道轮船在海中航行时,可以用方位角准确描述它的航行方向.
那你知道如何结合方位角等数据进行计算,帮助轮船在航行中远离危险吗?
三角函数的应用
1—
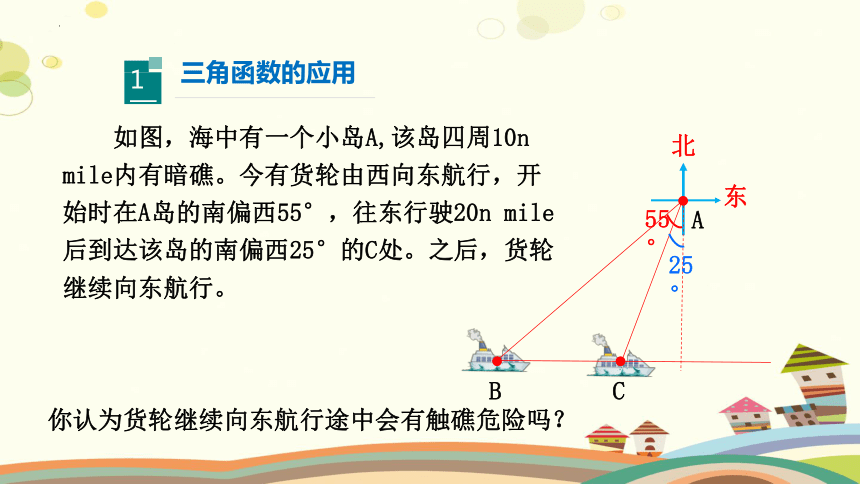
如图,海中有一个小岛A,该岛四周10n mile内有暗礁。今有货轮由西向东航行,开始时在A岛的南偏西55°,往东行驶20n mile后到达该岛的南偏西25°的C处。之后,货轮继续向东航行。
你认为货轮继续向东航行途中会有触礁危险吗?
东
北
A
B
C
25°
55°
A
B
55°
C
25°
你是怎样想的?与同伴进行交流.
20海里
D
解: 过A点作BC的垂线AD,则AD的长即为货轮距离小岛的最短距离.若AD>10海里,则货轮安全;反之则有触礁的危险.设AD=x.
x
Rt△ABD中,
Rt△ACD中,
∴BC=BD-CD=x·tan55°-x·tan25°
∴x= ≈20.79 海里
∴货轮继续向东航行途中没有触礁的危险.
1.运用锐角三角函数解决实际问题的方法:
(1)弄清题意,画出示意图;
(2)找出图形中的线段、角所表示的实际意义,并找到所要解决的问题;
(3)寻找要求解的直角三角形,有时需要作适当的辅助线;
(4)选择合适的边角关系式,进行有关锐角三角函数的计算;
(5)按照题目要求的精确度确定答案,并注明单位,作答.
典例精析
例1.如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高 (小明的身高忽略不计).
D
A
B
C
┌
50m
300
600
设CD长为x米,则∠ADC=60 ,∠BDC=30 ,
解:如图,根据题意知,∠A=300,∠DBC=600,AB=50m.求CD的长
在Rt△ADC中,tan60 =
在Rt△BDC中,tan30 =
∵AC-BC=AB
(
)
.
3
25
3
3
3
50
30
tan
60
tan
50
0
0
m
x
=
-
=
-
=
D
A
B
C
┌
50m
300
600
答:该塔约有 m高.
3
25
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?
65°
34°
P
B
C
A
议一议
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.8
在Rt△BPC中,∠B=34°
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130.23海里.
65°
34°
P
B
C
A
典例精析
例2.如图所示,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
总结
1.首先要弄清题意,结合实际问题中的示意图分清题目中的已知条件和所求结论.
2.找出问题中有几个直角三角形,或通过作辅助线构造直角三角形,把实际问题转化为解直角三角形的问题.
3.方程思想、转化思想的运用.
典例精析
例3.如图,一幢楼房AB背后有一台阶CD,台阶每层高0.2 m,且 AC=17.2 m,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10 m,现有一只小猫睡在台阶的MN这层上晒太阳( 取1.73).
(1)求楼房的高度约为多少米.
(2)过了一会儿,当α=45°时,
请说明理由.
(1)当α=60°时,在Rt△ABE中,
∵tan 60°=
∴AB=10·tan 60°=10 ≈10×1.73=17.3(m).
即楼房的高度约为17.3 m.
(2)当α=45°时,小猫仍可以晒到太阳.
理由如下:假设没有台阶,当α=45°时,从点B射
下的光线与地面AD的交点为点F,与射线CM的交点
为点H(如下图).
解:
∵∠BFA=45°,
∴tan 45°= =1,此时的影长AF=AB≈17.3m.
∴CF=AF-AC≈17.3-17.2=0.1(m).∴CH=CF≈0.1 m.
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳。
随堂练习
1.如图,一条斜坡长130 m,坡顶离水平地面的距离为50 m,那么这条斜坡的坡度是( )
A. B. C. D.
120 m
2.如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
A.5sin 36°米
B.5cos 36°米
C.5tan 36°米
D.10tan 36°米
3.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为________.
课堂总结
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直角三角形的有关性质解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
第一章 直角三角形的边角关系
第5节 三角函数的应用
学习目标
1.正确理解方位角、仰角和坡角的概念;(重点)
2.能运用解直角三角形知识解决方位角、仰角和坡角的问题.(难点)
情景引入
1.解直角三角形的意义:在直角三角形中,由已知元素求出所有未知元素的过程,叫做直角三角形.
2.直角三角形中诸元素之间的关系:
(1)三边之间的关系:a2+b2=c2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
把∠A换成∠B同样适用.
我们已经知道轮船在海中航行时,可以用方位角准确描述它的航行方向.
那你知道如何结合方位角等数据进行计算,帮助轮船在航行中远离危险吗?
三角函数的应用
1—
如图,海中有一个小岛A,该岛四周10n mile内有暗礁。今有货轮由西向东航行,开始时在A岛的南偏西55°,往东行驶20n mile后到达该岛的南偏西25°的C处。之后,货轮继续向东航行。
你认为货轮继续向东航行途中会有触礁危险吗?
东
北
A
B
C
25°
55°
A
B
55°
C
25°
你是怎样想的?与同伴进行交流.
20海里
D
解: 过A点作BC的垂线AD,则AD的长即为货轮距离小岛的最短距离.若AD>10海里,则货轮安全;反之则有触礁的危险.设AD=x.
x
Rt△ABD中,
Rt△ACD中,
∴BC=BD-CD=x·tan55°-x·tan25°
∴x= ≈20.79 海里
∴货轮继续向东航行途中没有触礁的危险.
1.运用锐角三角函数解决实际问题的方法:
(1)弄清题意,画出示意图;
(2)找出图形中的线段、角所表示的实际意义,并找到所要解决的问题;
(3)寻找要求解的直角三角形,有时需要作适当的辅助线;
(4)选择合适的边角关系式,进行有关锐角三角函数的计算;
(5)按照题目要求的精确度确定答案,并注明单位,作答.
典例精析
例1.如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高 (小明的身高忽略不计).
D
A
B
C
┌
50m
300
600
设CD长为x米,则∠ADC=60 ,∠BDC=30 ,
解:如图,根据题意知,∠A=300,∠DBC=600,AB=50m.求CD的长
在Rt△ADC中,tan60 =
在Rt△BDC中,tan30 =
∵AC-BC=AB
(
)
.
3
25
3
3
3
50
30
tan
60
tan
50
0
0
m
x
=
-
=
-
=
D
A
B
C
┌
50m
300
600
答:该塔约有 m高.
3
25
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?
65°
34°
P
B
C
A
议一议
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.8
在Rt△BPC中,∠B=34°
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130.23海里.
65°
34°
P
B
C
A
典例精析
例2.如图所示,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
总结
1.首先要弄清题意,结合实际问题中的示意图分清题目中的已知条件和所求结论.
2.找出问题中有几个直角三角形,或通过作辅助线构造直角三角形,把实际问题转化为解直角三角形的问题.
3.方程思想、转化思想的运用.
典例精析
例3.如图,一幢楼房AB背后有一台阶CD,台阶每层高0.2 m,且 AC=17.2 m,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10 m,现有一只小猫睡在台阶的MN这层上晒太阳( 取1.73).
(1)求楼房的高度约为多少米.
(2)过了一会儿,当α=45°时,
请说明理由.
(1)当α=60°时,在Rt△ABE中,
∵tan 60°=
∴AB=10·tan 60°=10 ≈10×1.73=17.3(m).
即楼房的高度约为17.3 m.
(2)当α=45°时,小猫仍可以晒到太阳.
理由如下:假设没有台阶,当α=45°时,从点B射
下的光线与地面AD的交点为点F,与射线CM的交点
为点H(如下图).
解:
∵∠BFA=45°,
∴tan 45°= =1,此时的影长AF=AB≈17.3m.
∴CF=AF-AC≈17.3-17.2=0.1(m).∴CH=CF≈0.1 m.
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳。
随堂练习
1.如图,一条斜坡长130 m,坡顶离水平地面的距离为50 m,那么这条斜坡的坡度是( )
A. B. C. D.
120 m
2.如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
A.5sin 36°米
B.5cos 36°米
C.5tan 36°米
D.10tan 36°米
3.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为________.
课堂总结
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直角三角形的有关性质解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
