等腰三角形复习题(2008中考)(陕西省西安市长安县)无答案
文档属性
| 名称 | 等腰三角形复习题(2008中考)(陕西省西安市长安县)无答案 |  | |
| 格式 | rar | ||
| 文件大小 | 123.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-27 12:59:00 | ||
图片预览

文档简介
等腰三角形复习题
1、 选择题。
1、(2008乌鲁木齐).某等腰三角形的两条边长分别为3cm和6cm,则它的周长为( )
A.9cm B.12cm C.15cm D.12cm或15cm
2、(2008年广东湛江市)如图2所示,已知等边三角形ABC的边长为,按图中所示的规律,用个这样的三角形镶嵌而成的四边形的周长是( )C
A. B. C. D.
3、(2008嘉兴市)已知等腰三角形的一个内角为,则这个等腰三角形的顶角为( )
A. B. C.或 D.或
4、(2008年安徽省)如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN等于( )
A. B. C. D.
5、(云南省2008年)已知,等腰三角形的一条边长等于,另一条边长等于,则此等腰三角形的周长是( )
A. B. C. D.或
6、(2008年龙岩市)如图,在边长为4的等边三角形ABC中,AD是BC边上的高,点E、F是AD上的两点,则图中阴影部分的面积是( )
A.4 B.3 C.2 D.
二、填空题。
1、(2008年郴州市)如图5,D是AB边上的中点,将沿过D的直线
折叠,使点A落在BC上F处,若,则 __________度.
2、(08年宁夏回族自治区)已知a、b、c为三个正整数,如果a+b+c=12,那么以a、b、c为边能组成的三角形是:①等腰三角形;②等边三角形;③直角三角形;④钝角三角形。以上符合条件的正确结论是 。(只填序号)
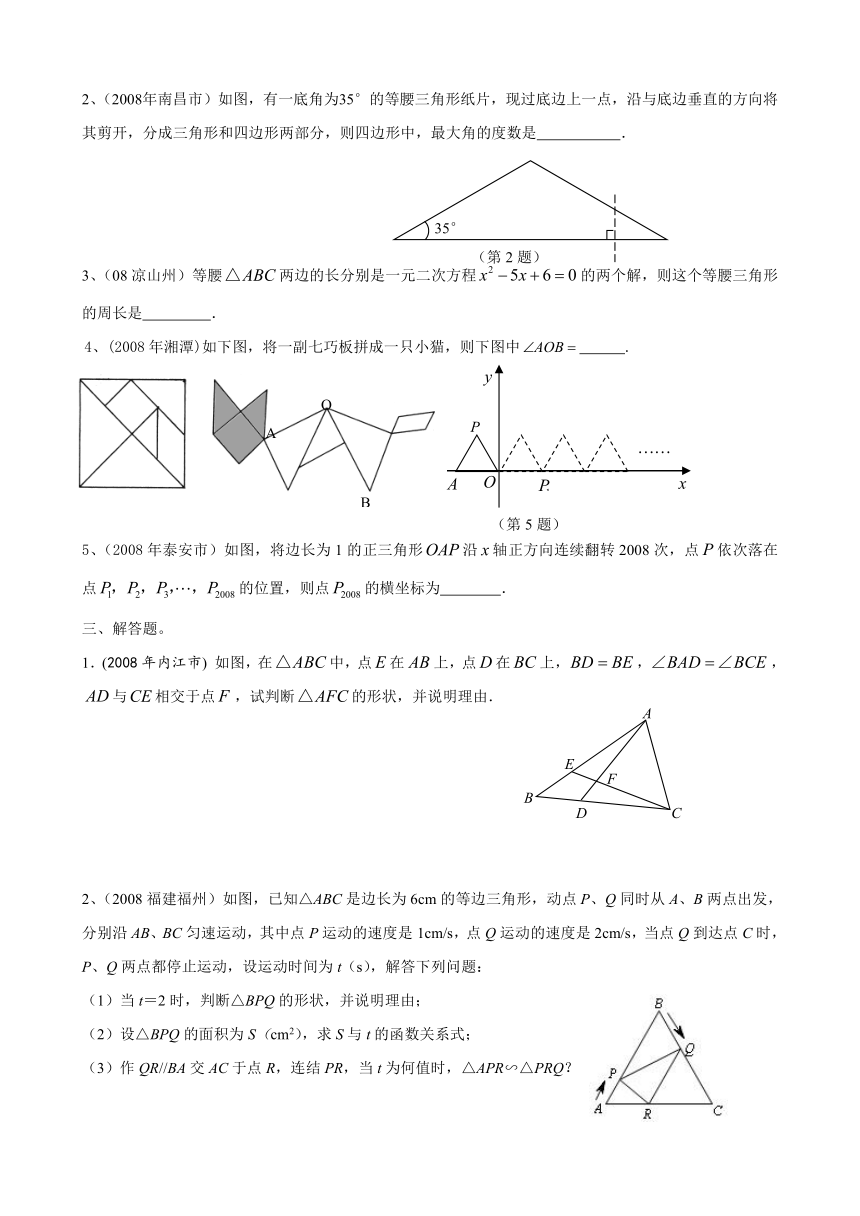
2、(2008年南昌市)如图,有一底角为35°的等腰三角形纸片,现过底边上一点,沿与底边垂直的方向将其剪开,分成三角形和四边形两部分,则四边形中,最大角的度数是 .
3、(08凉山州)等腰两边的长分别是一元二次方程的两个解,则这个等腰三角形的周长是 .
4、(2008年湘潭)如下图,将一副七巧板拼成一只小猫,则下图中 .
5、(2008年泰安市)如图,将边长为1的正三角形沿轴正方向连续翻转2008次,点依次落在点的位置,则点的横坐标为 .
三、解答题。
1.(2008年内江市) 如图,在中,点在上,点在上,,,与相交于点,试判断的形状,并说明理由.
2、(2008福建福州)如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?
3、 ( 2008年杭州市) 如图,在等腰△中,是底边上的高线,点是线段上不与端点重合的任意一点,连接交于点,连接交于点.
(1) 证明:;
(2) 证明:;
(3) 以线段和为边构成一个新的三角形(点与点重合于点),记△和△的面积分别为和,如果存在点,能使得 , 求∠的取值范围.
4、 (2008年·东莞市)如图5,在△ABC中,BC>AC, 点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF.
(1)求证:EF∥BC.
(2)若四边形BDFE的面积为6,求△ABD的面积.
5、(2008年益阳) (本题10分)△ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
Ⅰ.证明:△BDG≌△CEF;
Ⅱ. 探究:怎样在铁片上准确地画出正方形.
小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb
的两个问题中选择一个你喜欢的问题解答. 如果
两题都解,只以Ⅱa的解答记分.
Ⅱa. 小聪想:要画出正方形DEFG,只要能计算出
正方形的边长就能求出BD和CE的长,从而确定D点和
E点,再画正方形DEFG就容易了. 设△ABC的边长为2 ,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化) .
Ⅱb. 小明想:不求正方形的边长也能画出正方形. 具体作法是:
①在AB边上任取一点G’,如图作正方形G’D’E’F’;
②连结BF’并延长交AC于F;
③作FE∥F’E’交BC于E,FG∥F′G′交AB于G,
GD∥G’D’交BC于D,则四边形DEFG即为所求.
你认为小明的作法正确吗?说明理由.
图2
C
A
B
┅┅
第6题图
图5
(第2题)
35°
A
O
B
(第5题)
P
B
C
D
F
A
E
A
B
C
D
E
F
G
图10(1)
A
B
C
D
E
F
G
图10(2)
A
B
C
D
E
F
G
图10(3)
G′
F′
E′
D′
1、 选择题。
1、(2008乌鲁木齐).某等腰三角形的两条边长分别为3cm和6cm,则它的周长为( )
A.9cm B.12cm C.15cm D.12cm或15cm
2、(2008年广东湛江市)如图2所示,已知等边三角形ABC的边长为,按图中所示的规律,用个这样的三角形镶嵌而成的四边形的周长是( )C
A. B. C. D.
3、(2008嘉兴市)已知等腰三角形的一个内角为,则这个等腰三角形的顶角为( )
A. B. C.或 D.或
4、(2008年安徽省)如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN等于( )
A. B. C. D.
5、(云南省2008年)已知,等腰三角形的一条边长等于,另一条边长等于,则此等腰三角形的周长是( )
A. B. C. D.或
6、(2008年龙岩市)如图,在边长为4的等边三角形ABC中,AD是BC边上的高,点E、F是AD上的两点,则图中阴影部分的面积是( )
A.4 B.3 C.2 D.
二、填空题。
1、(2008年郴州市)如图5,D是AB边上的中点,将沿过D的直线
折叠,使点A落在BC上F处,若,则 __________度.
2、(08年宁夏回族自治区)已知a、b、c为三个正整数,如果a+b+c=12,那么以a、b、c为边能组成的三角形是:①等腰三角形;②等边三角形;③直角三角形;④钝角三角形。以上符合条件的正确结论是 。(只填序号)
2、(2008年南昌市)如图,有一底角为35°的等腰三角形纸片,现过底边上一点,沿与底边垂直的方向将其剪开,分成三角形和四边形两部分,则四边形中,最大角的度数是 .
3、(08凉山州)等腰两边的长分别是一元二次方程的两个解,则这个等腰三角形的周长是 .
4、(2008年湘潭)如下图,将一副七巧板拼成一只小猫,则下图中 .
5、(2008年泰安市)如图,将边长为1的正三角形沿轴正方向连续翻转2008次,点依次落在点的位置,则点的横坐标为 .
三、解答题。
1.(2008年内江市) 如图,在中,点在上,点在上,,,与相交于点,试判断的形状,并说明理由.
2、(2008福建福州)如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?
3、 ( 2008年杭州市) 如图,在等腰△中,是底边上的高线,点是线段上不与端点重合的任意一点,连接交于点,连接交于点.
(1) 证明:;
(2) 证明:;
(3) 以线段和为边构成一个新的三角形(点与点重合于点),记△和△的面积分别为和,如果存在点,能使得 , 求∠的取值范围.
4、 (2008年·东莞市)如图5,在△ABC中,BC>AC, 点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF.
(1)求证:EF∥BC.
(2)若四边形BDFE的面积为6,求△ABD的面积.
5、(2008年益阳) (本题10分)△ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
Ⅰ.证明:△BDG≌△CEF;
Ⅱ. 探究:怎样在铁片上准确地画出正方形.
小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb
的两个问题中选择一个你喜欢的问题解答. 如果
两题都解,只以Ⅱa的解答记分.
Ⅱa. 小聪想:要画出正方形DEFG,只要能计算出
正方形的边长就能求出BD和CE的长,从而确定D点和
E点,再画正方形DEFG就容易了. 设△ABC的边长为2 ,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化) .
Ⅱb. 小明想:不求正方形的边长也能画出正方形. 具体作法是:
①在AB边上任取一点G’,如图作正方形G’D’E’F’;
②连结BF’并延长交AC于F;
③作FE∥F’E’交BC于E,FG∥F′G′交AB于G,
GD∥G’D’交BC于D,则四边形DEFG即为所求.
你认为小明的作法正确吗?说明理由.
图2
C
A
B
┅┅
第6题图
图5
(第2题)
35°
A
O
B
(第5题)
P
B
C
D
F
A
E
A
B
C
D
E
F
G
图10(1)
A
B
C
D
E
F
G
图10(2)
A
B
C
D
E
F
G
图10(3)
G′
F′
E′
D′
同课章节目录
