实际问题与一元二次方程(4)(浙江省台州市温岭市)
文档属性
| 名称 | 实际问题与一元二次方程(4)(浙江省台州市温岭市) |

|
|
| 格式 | rar | ||
| 文件大小 | 341.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-06 00:00:00 | ||
图片预览





文档简介
课件16张PPT。22.3 实际问题与一元二次方程(四)行程问题:匀速运动匀变速运动复习回顾(1) S=VT(2) 匀变速运动中平均每秒速度变化值为:
(初速度-末速度) ÷变化时间(3) 匀变速运动中的平均速度为:
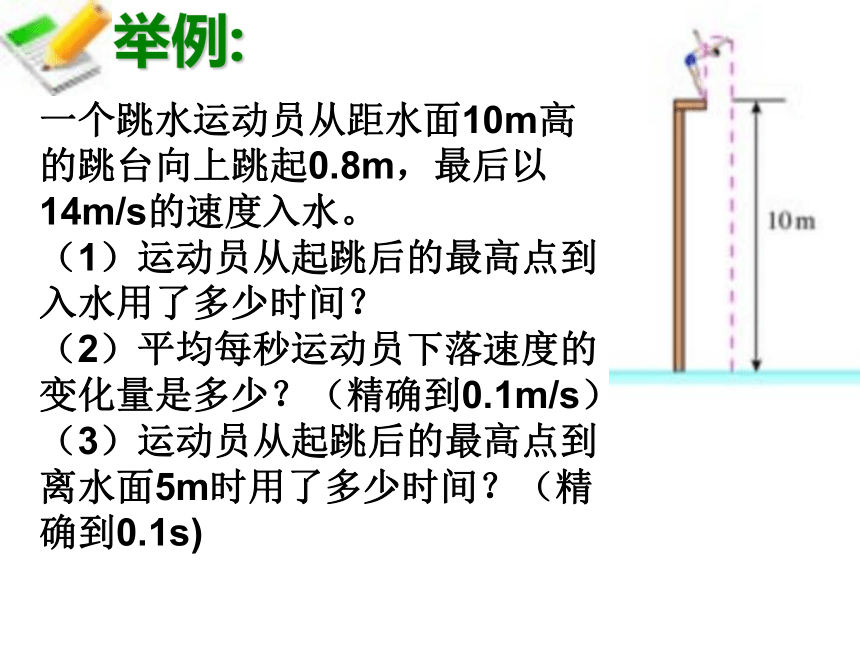
υ=(初速度+末速度)/2一个跳水运动员从距水面10m高的跳台向上跳起0.8m,最后以14m/s的速度入水。
(1)运动员从起跳后的最高点到入水用了多少时间?
(2)平均每秒运动员下落速度的变化量是多少?(精确到0.1m/s)
(3)运动员从起跳后的最高点到离水面5m时用了多少时间?(精确到0.1s)举例:利润问题 某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进价不变的情况下,若每千克涨价0.5元,日销售量将减少10千克,现该商场要保证每天盈利6000元,同时又让顾客得到实惠,那么每千克应涨价多少元?每千克的盈利×每天的销售量=每天的盈利解:设每千克应涨价x元.
由题意得:
(10+x)(500-20x)=6000
解得: x1=5,x2=10
因为为了使顾客得到实惠,所以x=5
答:每千克应涨价5元.(10+x)元(500-20x)千克6000元某零售商购进一批单价为16元的玩具,销售一段时间后,为了获得更多利润,商店决定提高销售价格,经过试验发现,若按每件20元的价格销售时每月能卖360件,若按每件25元的价格销信时,每月能卖210件,假设每月销售件数为y(件)是价格x(元/件)的一次函数。
(1)试求y与x之间的关系式;
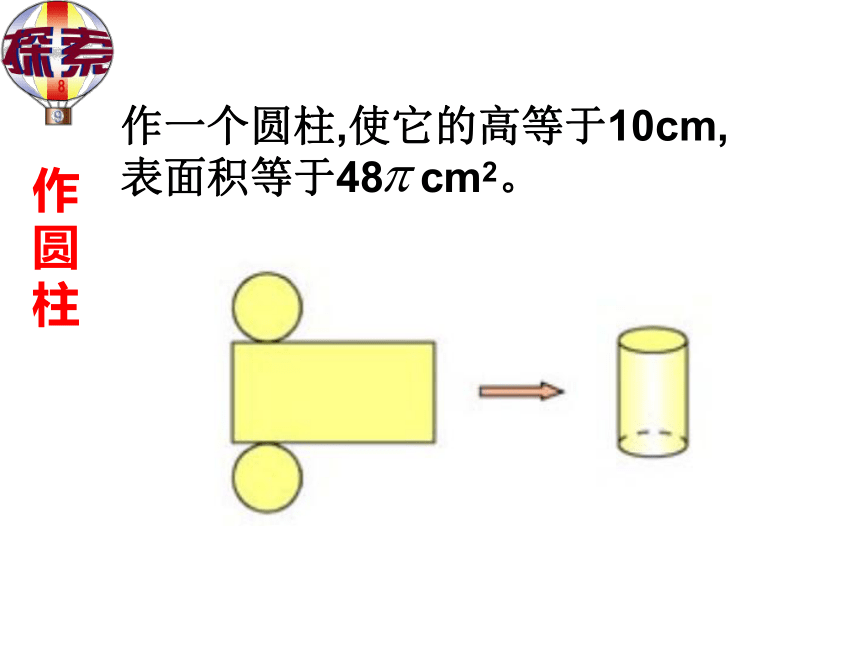
(2)在商品不积压且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?作一个圆柱,使它的高等于10cm,
表面积等于48 cm2。作圆柱变化率哈尔滨市政府为了申办2010年冬奥会,计划用两年的时间把城市绿地面积提高44%,每年比前一年提高的百分数相同。你能求出这个百分数吗?浓度问题一个容器盛满纯药液20升,第一次倒出若干升后,用水加满;第二次又倒出同样体积的溶液,这时容器里只剩下纯药液5升,每次倒出的液体是多少升?有变化的增长率问题王梅同学将100元压岁钱第一次按一年定期储蓄存入“少儿银行”,到期后将本金和利息支出,并将其中的50元捐给“希望工程”,剩余的又全部按一年定期存入,这时存款的年利率已下降到第一次存款时年利率的一半,到期后可得本金和利息共63元,求第一次存款时的年利率。 例: 如图,某海军基地位于A处,在其正南方向200海里处有一目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC上且恰好处于小岛D的正南方向.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰. (1)小岛D与小岛F相距多少海里?
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
∠C=450.解:(1)连接DF,则DF⊥BC.驶向胜利的彼岸CBF∟∟A 解:(2)设相遇时补给船航行了x海里,则DE=x海里,AB+BE=2x海里,EF=AB+BC-(AB+BE)-CF=(300-2x)海里.
在Rt△DEF中,根据勾股定理可得方程∴相遇时补给船大约航行了118.4海里练习:1、在矩形ABCD中,点P从点A沿AB向点B以每秒2cm的速度移动,点Q从点B开始沿BC向点C以每秒1cm的速度移动,AB=6cm,BC=4cm,若P、Q两点分别从A、B同时出发,问几秒后P、Q两点之间的距离为 cm?小结本节课应掌握:
运用路程=速度×时间,建立一元二次方程的数学模型,并解决一些实际问题.ABC如图,点C把线段AB分成两条线段AC和BC,如果 那么称线段AB被点C黄金分割(golden section),点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.为什么是0.618(1)
(初速度-末速度) ÷变化时间(3) 匀变速运动中的平均速度为:
υ=(初速度+末速度)/2一个跳水运动员从距水面10m高的跳台向上跳起0.8m,最后以14m/s的速度入水。
(1)运动员从起跳后的最高点到入水用了多少时间?
(2)平均每秒运动员下落速度的变化量是多少?(精确到0.1m/s)
(3)运动员从起跳后的最高点到离水面5m时用了多少时间?(精确到0.1s)举例:利润问题 某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进价不变的情况下,若每千克涨价0.5元,日销售量将减少10千克,现该商场要保证每天盈利6000元,同时又让顾客得到实惠,那么每千克应涨价多少元?每千克的盈利×每天的销售量=每天的盈利解:设每千克应涨价x元.
由题意得:
(10+x)(500-20x)=6000
解得: x1=5,x2=10
因为为了使顾客得到实惠,所以x=5
答:每千克应涨价5元.(10+x)元(500-20x)千克6000元某零售商购进一批单价为16元的玩具,销售一段时间后,为了获得更多利润,商店决定提高销售价格,经过试验发现,若按每件20元的价格销售时每月能卖360件,若按每件25元的价格销信时,每月能卖210件,假设每月销售件数为y(件)是价格x(元/件)的一次函数。
(1)试求y与x之间的关系式;
(2)在商品不积压且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?作一个圆柱,使它的高等于10cm,
表面积等于48 cm2。作圆柱变化率哈尔滨市政府为了申办2010年冬奥会,计划用两年的时间把城市绿地面积提高44%,每年比前一年提高的百分数相同。你能求出这个百分数吗?浓度问题一个容器盛满纯药液20升,第一次倒出若干升后,用水加满;第二次又倒出同样体积的溶液,这时容器里只剩下纯药液5升,每次倒出的液体是多少升?有变化的增长率问题王梅同学将100元压岁钱第一次按一年定期储蓄存入“少儿银行”,到期后将本金和利息支出,并将其中的50元捐给“希望工程”,剩余的又全部按一年定期存入,这时存款的年利率已下降到第一次存款时年利率的一半,到期后可得本金和利息共63元,求第一次存款时的年利率。 例: 如图,某海军基地位于A处,在其正南方向200海里处有一目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC上且恰好处于小岛D的正南方向.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰. (1)小岛D与小岛F相距多少海里?
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
∠C=450.解:(1)连接DF,则DF⊥BC.驶向胜利的彼岸CBF∟∟A 解:(2)设相遇时补给船航行了x海里,则DE=x海里,AB+BE=2x海里,EF=AB+BC-(AB+BE)-CF=(300-2x)海里.
在Rt△DEF中,根据勾股定理可得方程∴相遇时补给船大约航行了118.4海里练习:1、在矩形ABCD中,点P从点A沿AB向点B以每秒2cm的速度移动,点Q从点B开始沿BC向点C以每秒1cm的速度移动,AB=6cm,BC=4cm,若P、Q两点分别从A、B同时出发,问几秒后P、Q两点之间的距离为 cm?小结本节课应掌握:
运用路程=速度×时间,建立一元二次方程的数学模型,并解决一些实际问题.ABC如图,点C把线段AB分成两条线段AC和BC,如果 那么称线段AB被点C黄金分割(golden section),点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.为什么是0.618(1)
同课章节目录
