人教版 六年级上册 6 百分数(一) 解决问题(例5)课件(共28张PPT)
文档属性
| 名称 | 人教版 六年级上册 6 百分数(一) 解决问题(例5)课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
解决问题(例5)
第六单元 百分数
1.在理解数量关系的基础上,会用假设法解决有关“一个量两次增(减)后的变化幅度”的问题。
2.经历发现问题、提出问题、分析问题、解决问题的全过程,发展问题意识和探究意识。
学习目标
说一说下面题目中百分数的意义,再填( )。
1. 连环画的本数是故事书本数的37.5%。
2. 果园里苹果树的棵树比梨树多50%。
3. 一件商品在“十一”黄金周降价20%。
现价比原价降了20%
复习
“1”
( )×37.5%=连环画本数
“1”
苹果树比梨树多的棵数是梨树的50%
梨树棵数×( )= 苹果树比梨树多的棵数
“1”
( )×( )= 现价
故事书本数
50%
原价
1-20%
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
例5
读题,知道了什么?
阅读与理解
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
什么是变化幅度?
4月的变化幅度
5月的变化幅度
(数学书第88页)
例5
阅读与理解
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
例5
阅读与理解
降了20%后又涨回20%,价格不变。
降了。
涨了。
商品原来的价格未知啊,无法确定。
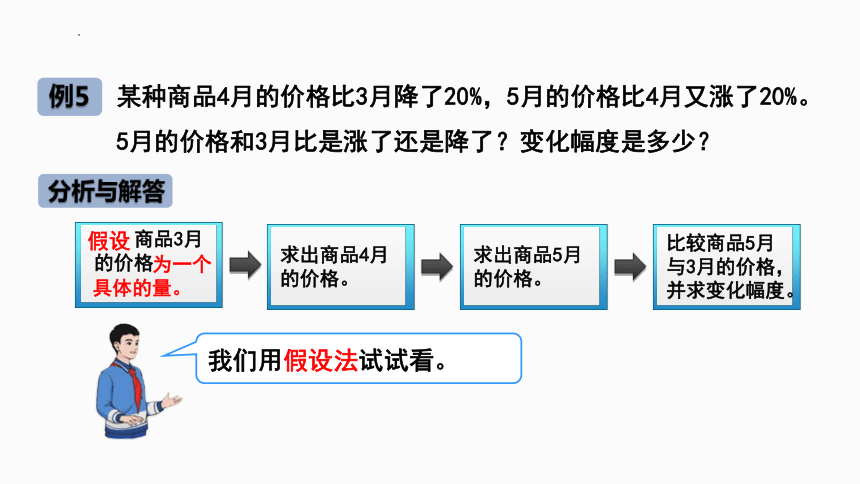
商品3月的价格
求出商品4月的价格。
求出商品5月的价格。
比较商品5月与3月的价格,并求变化幅度。
我们用假设法试试看。
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
例5
分析与解答
假设
为一个
具体的量。
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
(1)4月价格:
100 ×(1-20%)=100 ×0.8=80(元)
可以假设此商品3月的价格是100元。
(2)5月价格:
80 ×(1+20%)=80 ×1.2=96(元)
(4)变化幅度:
(100-96)÷100=4 ÷100=4%
答:5月的价格比3月降了,降低了4%。
(3)5月和3月价格比较:
96元<100元
(数学书第90页)
“1”
“1”
求5月价格比3月降了百分之几?
例5
分析与解答
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
例5
分析与解答
降了。
涨了。
商品原来的价格未知啊,无法确定。
降了20%后又涨回20%,价格不变。
?
×
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
“1”
“1”
降了20%后又涨回20%,价格不变。
4月的价格比3月降了20% → (3月价格)的20%
5月的价格比4月又涨了20%。 → (4月价格)的20%
(1)4月价格:
100 ×(1-20%)=100 ×0.8=80(元)
(2)5月价格:
80 ×(1+20%)=80 ×1.2=96(元)
例5
分析与解答
×
?
还能假设3月的价格是多少呢?
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
例5
分析与解答
(1)4月价格:
1000 ×(1-20%)=1000 ×0.8=800(元)
(2)5月价格:
800 ×(1+20%)=800 ×1.2=960(元)
(4)变化幅度:
(1000-960)÷1000=40 ÷1000=4%
答:5月的价格比3月降了,降低了4%。
(3)5月和3月价格比较:
960元<1000元
可以假设此商品3月的价格是1000元。
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
分析与解答
例5
比一比,你有什么发现?
假设3月的价格 4月的价格 5月的价格 变化幅度
100元 80 96 降低了4%
1000元 800 960 降低了4%
数学书第42页例7
(1)4月价格:
1 ×(1-20%)=1 ×0.8=0.8
(2)5月价格:
0.8 ×(1+20%)=0.8 ×1.2=0.96
(4)变化幅度:
(1-0.96)÷1=0.04 = 4%
答:5月的价格比3月降了,降低了4%。
(3)5月和3月价格比较:
0.96 < 1
也可以直接假设此商品3月的价格是1。
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
分析与解答
例5
也可以直接假设此商品3月的价格是1。
“1”不是1元,但可以代表“1元”“100元”“1000元”……
1×(1-20%)×(1+20%)=0.96
0.96 < 1
(1-0.96)÷1=0.04=4%
答:5月的价格比3月降了,降低了4%。
4月的价格
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
分析与解答
例5
5月的价格
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
(1)4月价格:
a ×(1-20%)= a ×0.8=0.8 a
(2)5月价格:
0.8 a ×(1+20%)=0.8a ×1.2=0.96 a
(4)变化幅度:
( a -0.96 a )÷ a =0.04 = 4%
答:5月的价格比3月降了,降低了4%。
(3)5月和3月价格比较:
0.96 a < a
如果此商品3月的价格是a(a>0)元呢?结论是否一致?
例5
回顾与反思
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
如果此商品3月的价格是a(a>0)元呢?结论是否一致?
结论一致!
a ×(1-20%)×(1+20%)=0.96 a
0.96 a < a
( a -0.96a )÷ a =0.04=4%
答:5月的价格比3月降了,降低了4%。
例5
回顾与反思
假设3月的价格 4月的价格 5月的价格 变化幅度
100元 80 96 降低了4%
1000元 800 960 降低了4%
1 0.8 0.96 降低了4%
a 0.8a 0.96a 降低了4%
(数学书第89页“做一做”第3题)
1.某电视机厂计划某种型号的电视机比去年增产50%,
实际又比计划的产量多生产了10%。此型号的电视机
今年的实际产量是去年的百分之多少?
(1)今年计划产量:
100×(1+50%)=100×1.5=150(台)
答:此型号的电视机今年的实际产量是去年的165%。
(2)今年实际产量:
150×(1+10%)=150×1.1=165(台)
(3)165÷100=1.65 = 165%
练一练
“1”
“1”
方法一:假设去年产量是100台。
方法二:假设去年产量是1。
1×(1+50%)×(1+10%)=1.65
计划产量
实际产量
1.65 ÷ 1 = 165%
(数学书第89页“做一做”第3题)
1.某电视机厂计划某种型号的电视机比去年增产50%,
实际又比计划的产量多生产了10%。此型号的电视机
今年的实际产量是去年的百分之多少?
练一练
“1”
“1”
答:今年的实际产量是去年的165%。
2.9月初鸡蛋价格比7月初涨了还是跌了?涨跌幅度是多少?
(数学书第91页第11题)
练一练
8月初鸡蛋价格比7月初上涨了10%。
9月初又比8月初回落了15%。
2.9月初鸡蛋价格比7月初涨了还是
跌了?涨跌幅度是多少?
(数学书第91页第11题)
1×(1+10%) ×(1-15%)=0.935
练一练
假设7月初的价格是1。
8月初价格
9月初价格
0.935< 1
(1-0.935)÷1=0.065=6.5%
答:9月初鸡蛋价格比7月初跌了,跌了6.5%。
“1”
“1”
小林买一台电视机,她看上的电视机两家商场都有售,且原价相同。近来两家商场都在做促销活动。小林在( )买电视机比较划算。
A商场
“比原价降低了20%”。
B商场
“上个月比原价降低10%,这个月在上个月的基础上再次降低10%”。
A. A商场 B. B商场 C.无法判断
练一练
B商场:5000×(1-10%)×(1-10%)=4050(元)
小林在A商场买电视机比较划算。
假设这台电视机原来的价格为5000元。
A商场:5000×(1-20%)=4000(元)
4000元<4050元
A商场
“比原价降低了20%”。
B商场
“上个月比原价降低10%,这个月在上个月的基础上再次降低10%”。
小林买一台电视机,她看上的电视机两家商场都有售,且原价相同。近来两家商场都在做促销活动。小林在( )买电视机比较划算。
A商场
“比原价降低了20%”。
B商场
“上个月比原价降低10%,这个月在上个月的基础上再次降低10%”。
A. A商场 B. B商场 C.无法判断
练一练
A
运用了“求比一个数多(或少)百分之几的数是多少”的知识解决新问题。
课堂小结
可以直接假设商品原来的价格是1。
要找准分率的单位“1”。
解决问题(例5)
第六单元 百分数
1.在理解数量关系的基础上,会用假设法解决有关“一个量两次增(减)后的变化幅度”的问题。
2.经历发现问题、提出问题、分析问题、解决问题的全过程,发展问题意识和探究意识。
学习目标
说一说下面题目中百分数的意义,再填( )。
1. 连环画的本数是故事书本数的37.5%。
2. 果园里苹果树的棵树比梨树多50%。
3. 一件商品在“十一”黄金周降价20%。
现价比原价降了20%
复习
“1”
( )×37.5%=连环画本数
“1”
苹果树比梨树多的棵数是梨树的50%
梨树棵数×( )= 苹果树比梨树多的棵数
“1”
( )×( )= 现价
故事书本数
50%
原价
1-20%
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
例5
读题,知道了什么?
阅读与理解
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
什么是变化幅度?
4月的变化幅度
5月的变化幅度
(数学书第88页)
例5
阅读与理解
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
例5
阅读与理解
降了20%后又涨回20%,价格不变。
降了。
涨了。
商品原来的价格未知啊,无法确定。
商品3月的价格
求出商品4月的价格。
求出商品5月的价格。
比较商品5月与3月的价格,并求变化幅度。
我们用假设法试试看。
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
例5
分析与解答
假设
为一个
具体的量。
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
(1)4月价格:
100 ×(1-20%)=100 ×0.8=80(元)
可以假设此商品3月的价格是100元。
(2)5月价格:
80 ×(1+20%)=80 ×1.2=96(元)
(4)变化幅度:
(100-96)÷100=4 ÷100=4%
答:5月的价格比3月降了,降低了4%。
(3)5月和3月价格比较:
96元<100元
(数学书第90页)
“1”
“1”
求5月价格比3月降了百分之几?
例5
分析与解答
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
例5
分析与解答
降了。
涨了。
商品原来的价格未知啊,无法确定。
降了20%后又涨回20%,价格不变。
?
×
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
“1”
“1”
降了20%后又涨回20%,价格不变。
4月的价格比3月降了20% → (3月价格)的20%
5月的价格比4月又涨了20%。 → (4月价格)的20%
(1)4月价格:
100 ×(1-20%)=100 ×0.8=80(元)
(2)5月价格:
80 ×(1+20%)=80 ×1.2=96(元)
例5
分析与解答
×
?
还能假设3月的价格是多少呢?
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
例5
分析与解答
(1)4月价格:
1000 ×(1-20%)=1000 ×0.8=800(元)
(2)5月价格:
800 ×(1+20%)=800 ×1.2=960(元)
(4)变化幅度:
(1000-960)÷1000=40 ÷1000=4%
答:5月的价格比3月降了,降低了4%。
(3)5月和3月价格比较:
960元<1000元
可以假设此商品3月的价格是1000元。
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
分析与解答
例5
比一比,你有什么发现?
假设3月的价格 4月的价格 5月的价格 变化幅度
100元 80 96 降低了4%
1000元 800 960 降低了4%
数学书第42页例7
(1)4月价格:
1 ×(1-20%)=1 ×0.8=0.8
(2)5月价格:
0.8 ×(1+20%)=0.8 ×1.2=0.96
(4)变化幅度:
(1-0.96)÷1=0.04 = 4%
答:5月的价格比3月降了,降低了4%。
(3)5月和3月价格比较:
0.96 < 1
也可以直接假设此商品3月的价格是1。
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
分析与解答
例5
也可以直接假设此商品3月的价格是1。
“1”不是1元,但可以代表“1元”“100元”“1000元”……
1×(1-20%)×(1+20%)=0.96
0.96 < 1
(1-0.96)÷1=0.04=4%
答:5月的价格比3月降了,降低了4%。
4月的价格
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
分析与解答
例5
5月的价格
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
(1)4月价格:
a ×(1-20%)= a ×0.8=0.8 a
(2)5月价格:
0.8 a ×(1+20%)=0.8a ×1.2=0.96 a
(4)变化幅度:
( a -0.96 a )÷ a =0.04 = 4%
答:5月的价格比3月降了,降低了4%。
(3)5月和3月价格比较:
0.96 a < a
如果此商品3月的价格是a(a>0)元呢?结论是否一致?
例5
回顾与反思
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
如果此商品3月的价格是a(a>0)元呢?结论是否一致?
结论一致!
a ×(1-20%)×(1+20%)=0.96 a
0.96 a < a
( a -0.96a )÷ a =0.04=4%
答:5月的价格比3月降了,降低了4%。
例5
回顾与反思
假设3月的价格 4月的价格 5月的价格 变化幅度
100元 80 96 降低了4%
1000元 800 960 降低了4%
1 0.8 0.96 降低了4%
a 0.8a 0.96a 降低了4%
(数学书第89页“做一做”第3题)
1.某电视机厂计划某种型号的电视机比去年增产50%,
实际又比计划的产量多生产了10%。此型号的电视机
今年的实际产量是去年的百分之多少?
(1)今年计划产量:
100×(1+50%)=100×1.5=150(台)
答:此型号的电视机今年的实际产量是去年的165%。
(2)今年实际产量:
150×(1+10%)=150×1.1=165(台)
(3)165÷100=1.65 = 165%
练一练
“1”
“1”
方法一:假设去年产量是100台。
方法二:假设去年产量是1。
1×(1+50%)×(1+10%)=1.65
计划产量
实际产量
1.65 ÷ 1 = 165%
(数学书第89页“做一做”第3题)
1.某电视机厂计划某种型号的电视机比去年增产50%,
实际又比计划的产量多生产了10%。此型号的电视机
今年的实际产量是去年的百分之多少?
练一练
“1”
“1”
答:今年的实际产量是去年的165%。
2.9月初鸡蛋价格比7月初涨了还是跌了?涨跌幅度是多少?
(数学书第91页第11题)
练一练
8月初鸡蛋价格比7月初上涨了10%。
9月初又比8月初回落了15%。
2.9月初鸡蛋价格比7月初涨了还是
跌了?涨跌幅度是多少?
(数学书第91页第11题)
1×(1+10%) ×(1-15%)=0.935
练一练
假设7月初的价格是1。
8月初价格
9月初价格
0.935< 1
(1-0.935)÷1=0.065=6.5%
答:9月初鸡蛋价格比7月初跌了,跌了6.5%。
“1”
“1”
小林买一台电视机,她看上的电视机两家商场都有售,且原价相同。近来两家商场都在做促销活动。小林在( )买电视机比较划算。
A商场
“比原价降低了20%”。
B商场
“上个月比原价降低10%,这个月在上个月的基础上再次降低10%”。
A. A商场 B. B商场 C.无法判断
练一练
B商场:5000×(1-10%)×(1-10%)=4050(元)
小林在A商场买电视机比较划算。
假设这台电视机原来的价格为5000元。
A商场:5000×(1-20%)=4000(元)
4000元<4050元
A商场
“比原价降低了20%”。
B商场
“上个月比原价降低10%,这个月在上个月的基础上再次降低10%”。
小林买一台电视机,她看上的电视机两家商场都有售,且原价相同。近来两家商场都在做促销活动。小林在( )买电视机比较划算。
A商场
“比原价降低了20%”。
B商场
“上个月比原价降低10%,这个月在上个月的基础上再次降低10%”。
A. A商场 B. B商场 C.无法判断
练一练
A
运用了“求比一个数多(或少)百分之几的数是多少”的知识解决新问题。
课堂小结
可以直接假设商品原来的价格是1。
要找准分率的单位“1”。
