24.1.3 弧、弦、圆心角 培优练习(无答案) 人教版数学九年级上册
文档属性
| 名称 | 24.1.3 弧、弦、圆心角 培优练习(无答案) 人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 655.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 21:25:05 | ||
图片预览



文档简介
24.1.3 弧、弦、圆心角 培优练习
一、选择题
1.同圆中,两条弦长分别为a和b,它们的弦心距分别为c和d,若c>d,则有( )
A.a>b B.a<b C.a=b D.不能确定
2.如图,点A、B、C在⊙O上,∠AOC=70°,则∠ABC的度数为( )
A.10°; B.20°; C.35°; D.55°.
3.如图,在⊙O中,AB是⊙O的直径,AB=10,==,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=30°;②∠DOB=2∠CED;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
4.如图,已知AB是⊙O的直径,BC=CD=DE,∠BOC=40°,那么∠AOE等于( )
A.40° B.50° C.60° D.120°
5.如图,四边形ABCD内接于直径为6的⊙O,AB=AC,E是弦AC和直径BD的交点,ED=,则弦AC的长为( )
A.2 B.3 C.2 D.2
6.如图,、、度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
A.55° B.60° C.65° D.70°
7.如图,为的直径,点C是弧的中点.过点C作于点G,交于点D,若,则的半径长是( )
A.5 B.6.5 C.7.5 D.8
8.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比,下面是同一个任务进行到不同阶段时进度条的示意图:
当任务完成的百分比为时,线段的长度记为.下列描述正确的是( )
A.当时, B.当时,
C.当时, D.当时,
9.如图,在⊙O中,弦AB=CD,图中的线段、角、弧分别具有相等关系的量共有(不包括AB=CD)( )
A.10组 B.7组 C.6组 D.5组
10.已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
①∠PAD=∠PDA=60 ; ②△PAO≌△ADE;③PO=r;④AO∶OP∶PA=1∶∶.
A.①④ B.②③ C.③④ D.①③④
二、填空题
1.如图,AB是⊙O的直径,D.C是弧BE的三等分点,∠COD=32°,则∠E的度数是 .
2.如图,点C是直径的三等分点,点D是弧的三等分点,若直径,则的长为 .
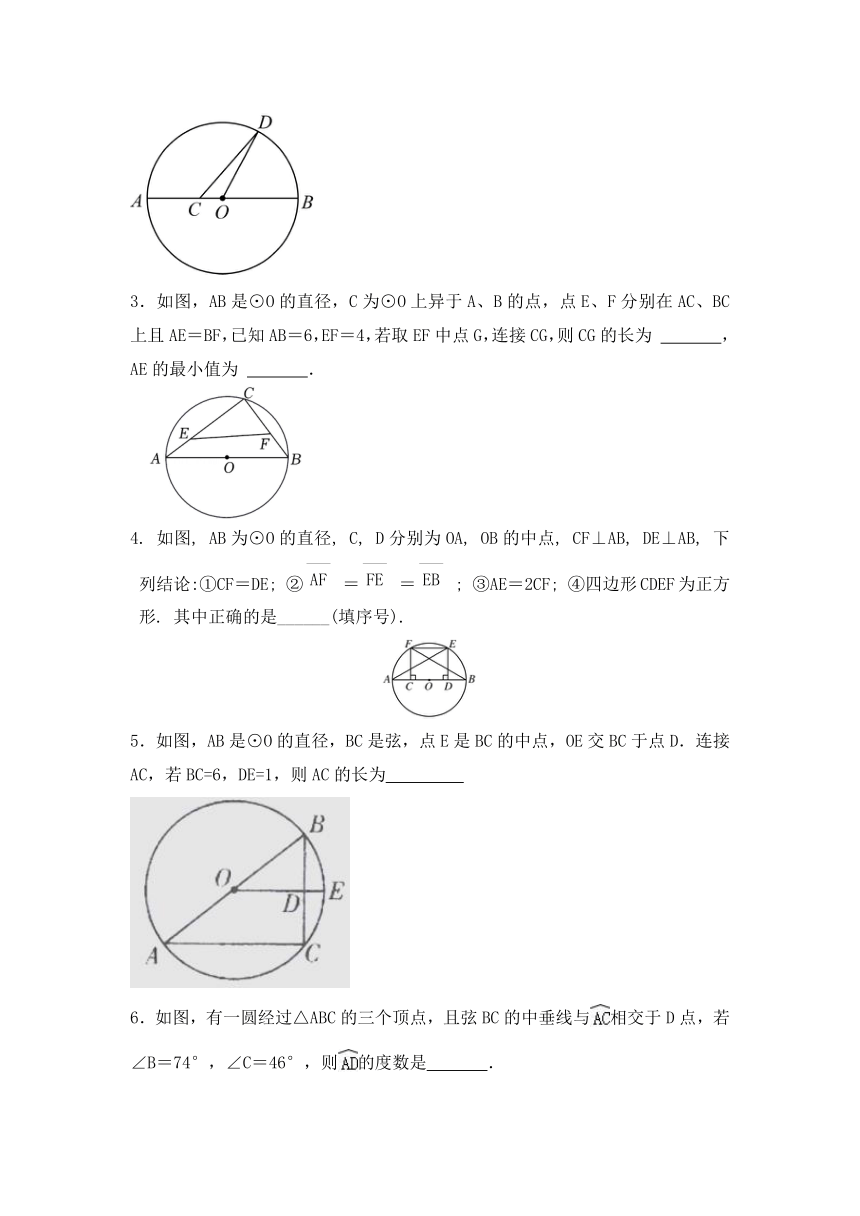
3.如图,AB是⊙O的直径,C为⊙O上异于A、B的点,点E、F分别在AC、BC上且AE=BF,已知AB=6,EF=4,若取EF中点G,连接CG,则CG的长为 ,AE的最小值为 .
4. 如图, AB为⊙O的直径, C, D分别为OA, OB的中点, CF⊥AB, DE⊥AB, 下列结论:①CF=DE; ②==; ③AE=2CF; ④四边形CDEF为正方形. 其中正确的是______(填序号).
5.如图,AB是⊙O的直径,BC是弦,点E是BC的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为
6.如图,有一圆经过△ABC的三个顶点,且弦BC的中垂线与相交于D点,若∠B=74°,∠C=46°,则的度数是 .
7.如图,AB是⊙O的弦,连接BO,作AC⊥BO交BO的延长线于点C,已知OC=,BO=2,点D是的中点,连接CD,则CD的长为 .
8.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是 cm.
解答题
1.在中,弦,求证.
2.如图,AB是⊙O的直径,点C,E都在⊙O上,OC⊥AB,=2,DE∥AB交OC于点D,延长OC至点F,使FC=OC,连接EF.
(1)求证:CD=OD.
(2)若⊙O的直径是4,求EF的长.
3. 如图,、是上两点,点是弧的中点,.
求证:四边形是菱形;
延长至使得,连接,,求的半径.
4.如图,是的两条弦.
(1)如果,那么__________,___________.
(2)如果,那么__________,___________.
(3)如果,那么__________,___________.
(4)如果,垂足分别为与相等吗?为什么?
5.请阅读下面材料,并完成相应的任务.
阿基米德(,公元前287-公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.
阿基米德折弦定理:如图1,和是的两条弦(即折线是圆的一条折弦),.M是的中点,则从点M向所作垂线的垂足D是折弦的中点,即.
这个定理有很多证明方法,下面是运用“垂线法”证明的部分证明过程.
证明:如图2,过点M作射线AB,垂足为点H,连接.
∵M是的中点,
∴.
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,已知等边三角形内接于,D为上一点,.于点E,,连接,求的周长.
一、选择题
1.同圆中,两条弦长分别为a和b,它们的弦心距分别为c和d,若c>d,则有( )
A.a>b B.a<b C.a=b D.不能确定
2.如图,点A、B、C在⊙O上,∠AOC=70°,则∠ABC的度数为( )
A.10°; B.20°; C.35°; D.55°.
3.如图,在⊙O中,AB是⊙O的直径,AB=10,==,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=30°;②∠DOB=2∠CED;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
4.如图,已知AB是⊙O的直径,BC=CD=DE,∠BOC=40°,那么∠AOE等于( )
A.40° B.50° C.60° D.120°
5.如图,四边形ABCD内接于直径为6的⊙O,AB=AC,E是弦AC和直径BD的交点,ED=,则弦AC的长为( )
A.2 B.3 C.2 D.2
6.如图,、、度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
A.55° B.60° C.65° D.70°
7.如图,为的直径,点C是弧的中点.过点C作于点G,交于点D,若,则的半径长是( )
A.5 B.6.5 C.7.5 D.8
8.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比,下面是同一个任务进行到不同阶段时进度条的示意图:
当任务完成的百分比为时,线段的长度记为.下列描述正确的是( )
A.当时, B.当时,
C.当时, D.当时,
9.如图,在⊙O中,弦AB=CD,图中的线段、角、弧分别具有相等关系的量共有(不包括AB=CD)( )
A.10组 B.7组 C.6组 D.5组
10.已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
①∠PAD=∠PDA=60 ; ②△PAO≌△ADE;③PO=r;④AO∶OP∶PA=1∶∶.
A.①④ B.②③ C.③④ D.①③④
二、填空题
1.如图,AB是⊙O的直径,D.C是弧BE的三等分点,∠COD=32°,则∠E的度数是 .
2.如图,点C是直径的三等分点,点D是弧的三等分点,若直径,则的长为 .
3.如图,AB是⊙O的直径,C为⊙O上异于A、B的点,点E、F分别在AC、BC上且AE=BF,已知AB=6,EF=4,若取EF中点G,连接CG,则CG的长为 ,AE的最小值为 .
4. 如图, AB为⊙O的直径, C, D分别为OA, OB的中点, CF⊥AB, DE⊥AB, 下列结论:①CF=DE; ②==; ③AE=2CF; ④四边形CDEF为正方形. 其中正确的是______(填序号).
5.如图,AB是⊙O的直径,BC是弦,点E是BC的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为
6.如图,有一圆经过△ABC的三个顶点,且弦BC的中垂线与相交于D点,若∠B=74°,∠C=46°,则的度数是 .
7.如图,AB是⊙O的弦,连接BO,作AC⊥BO交BO的延长线于点C,已知OC=,BO=2,点D是的中点,连接CD,则CD的长为 .
8.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是 cm.
解答题
1.在中,弦,求证.
2.如图,AB是⊙O的直径,点C,E都在⊙O上,OC⊥AB,=2,DE∥AB交OC于点D,延长OC至点F,使FC=OC,连接EF.
(1)求证:CD=OD.
(2)若⊙O的直径是4,求EF的长.
3. 如图,、是上两点,点是弧的中点,.
求证:四边形是菱形;
延长至使得,连接,,求的半径.
4.如图,是的两条弦.
(1)如果,那么__________,___________.
(2)如果,那么__________,___________.
(3)如果,那么__________,___________.
(4)如果,垂足分别为与相等吗?为什么?
5.请阅读下面材料,并完成相应的任务.
阿基米德(,公元前287-公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.
阿基米德折弦定理:如图1,和是的两条弦(即折线是圆的一条折弦),.M是的中点,则从点M向所作垂线的垂足D是折弦的中点,即.
这个定理有很多证明方法,下面是运用“垂线法”证明的部分证明过程.
证明:如图2,过点M作射线AB,垂足为点H,连接.
∵M是的中点,
∴.
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,已知等边三角形内接于,D为上一点,.于点E,,连接,求的周长.
同课章节目录
