第四章 图形的相似 单元培优测试题(无答案) 北师大版九年级数学上册
文档属性
| 名称 | 第四章 图形的相似 单元培优测试题(无答案) 北师大版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 236.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 22:23:28 | ||
图片预览

文档简介
第四章 图形的相似 单元培优测试题 2023-2024学年北师大版九年级数学上册
一、选择题(每小题3分,共30分).
1、若,则等于( )
A. B. C. D.
2、如图,由下列条件不能判定△ABC与△ADE相似的是( )
A. B.∠B=∠ADE C. D.∠C=∠AED
3、如图,△ABC∽△ACP,若∠A=75°,∠APC=65°,则∠B的大小为( )
A.40° B.50° C.65° D.75°
4、如图,∠ACB=∠ADC=90°,BC=a,AC=b,AD=c,要使⊿ABC∽⊿CAD,只要CD等于( )
A. B. C. D.
5、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面直径为1.2米,桌面离地面1米.若灯泡离地面3 米,则地面上阴影部分的面积为( )
A.0..36π米2 B. 0.81π米2 C.2π米2 D.3. 24π米2
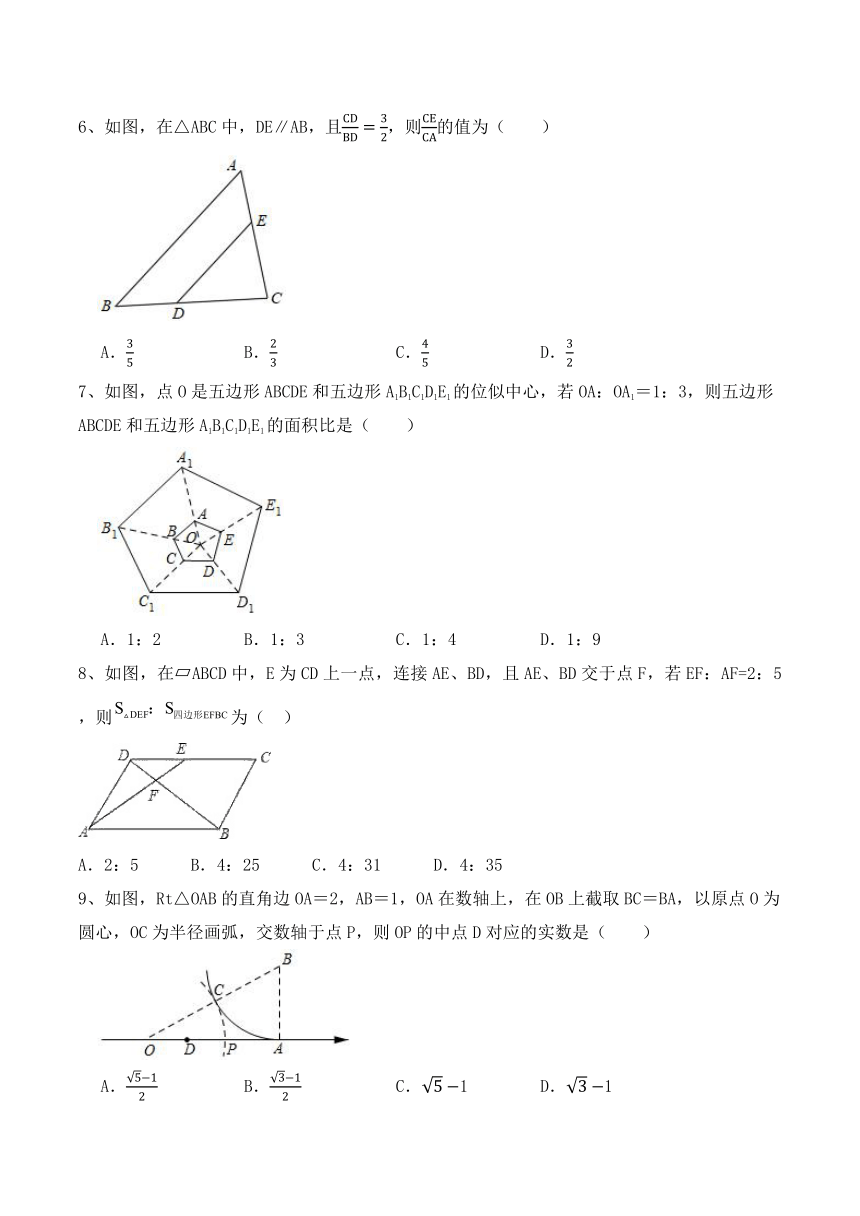
6、如图,在△ABC中,DE∥AB,且,则的值为( )
A. B. C. D.
7、如图,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA:OA1=1:3,则五边形ABCDE和五边形A1B1C1D1E1的面积比是( )
A.1:2 B.1:3 C.1:4 D.1:9
8、如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,若EF:AF=2:5,则为( )
A.2:5 B.4:25 C.4:31 D.4:35
9、如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A. B. C.1 D.1
10、如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为,,,.动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.作于点G,则运动过程中,AG的最大值为( )
A. B. C. D.8
二、填空题(每小题3分,共18分).
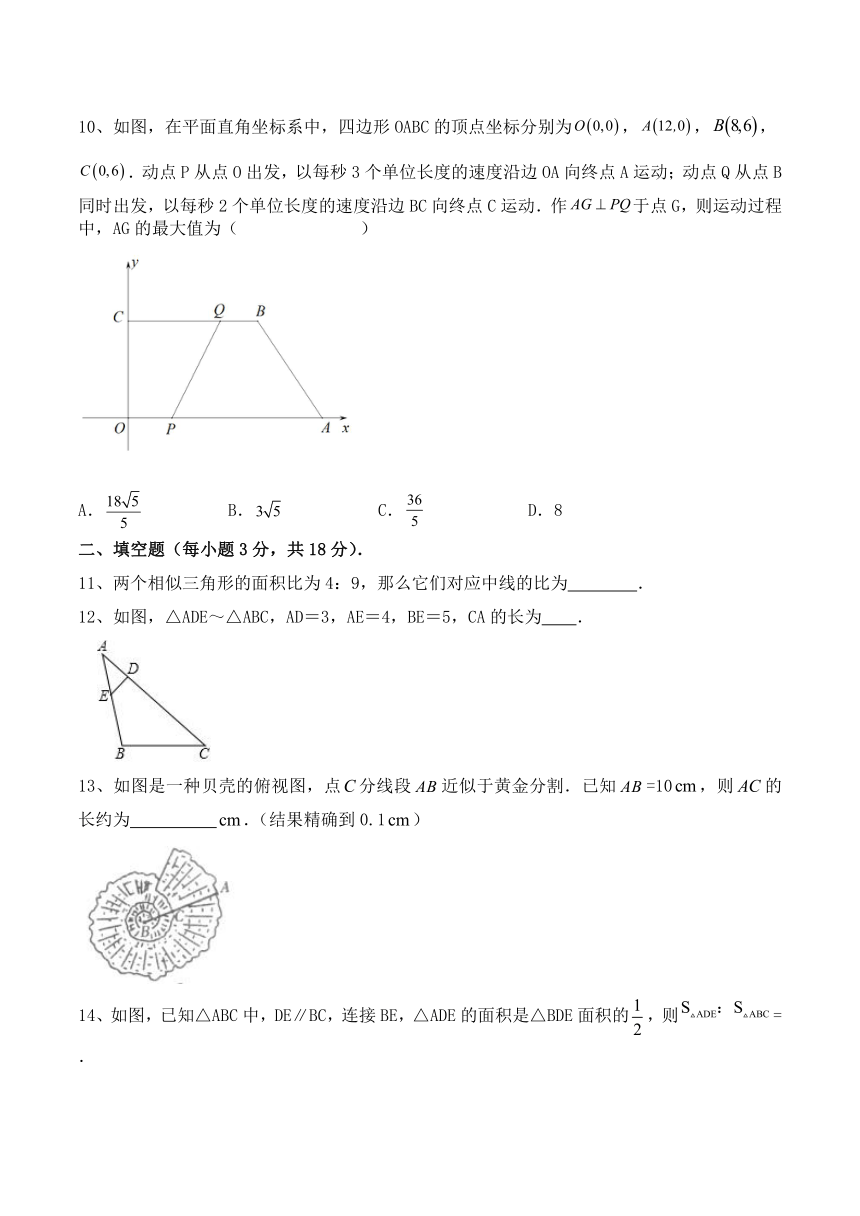
11、两个相似三角形的面积比为4:9,那么它们对应中线的比为 .
12、如图,△ADE~△ABC,AD=3,AE=4,BE=5,CA的长为 .
13、如图是一种贝壳的俯视图,点分线段近似于黄金分割.已知=10,则的长约为 .(结果精确到0.1)
14、如图,已知△ABC中,DE∥BC,连接BE,△ADE的面积是△BDE面积的,则= .
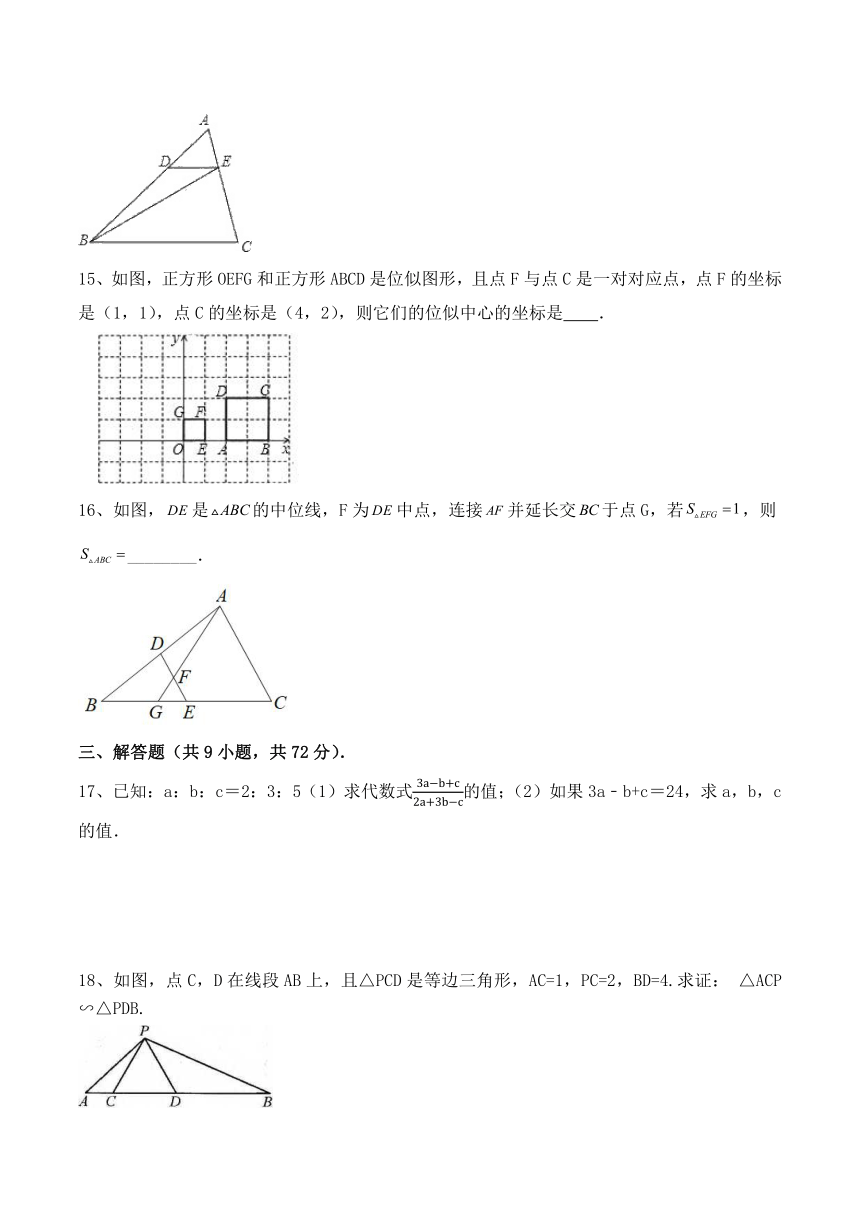
15、如图,正方形OEFG和正方形ABCD是位似图形,且点F与点C是一对对应点,点F的坐标是(1,1),点C的坐标是(4,2),则它们的位似中心的坐标是 .
16、如图,是的中位线,F为中点,连接并延长交于点G,若,则________.
三、解答题(共9小题,共72分).
17、已知:a:b:c=2:3:5(1)求代数式的值;(2)如果3a﹣b+c=24,求a,b,c的值.
18、如图,点C,D在线段AB上,且△PCD是等边三角形,AC=1,PC=2,BD=4.求证: △ACP∽△PDB.
19、为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面1.6米,标杆高为3.2米,且BC=2米,CD=6米,求树ED的高.
20、如图,AD是△ABC的中线,E是AD上一点,AE:AD=1:4,BE的延长线交AC于F,求AF:CF的值.
21、如图,在□ABCD中,E是 BC 边上一点,且 BE=EC,BD和AE 相交于F点.
(1)求△BEF 的周长与△AFD 的周长之比;
(2)若△BEF 的面积S△BEF=6 cm ,求△AFD 的面积.
22、小明放学回家途经一个小广场,广场的中央有一个羽毛球场地,场地的周围是片平坦的草坪,同时与羽毛球网在同一平面内有两个一样高的路灯,小明想测量路灯的高度AB,但是他没有带任何测量工具.于是,小明调整自己的步伐,尽量使得每一步步长相同,小明测出离路灯较近的网杆在路灯AB下的影长DF为2步,离路灯较远的网杆在路灯AB下的影长EC为5步,回家后小明上网查资料得到羽毛球网杆高DM=NE=1.55米,网长MN=61米,同时测得1步≈1米,求路灯的高度(结果保留一位小数).
23、如图,在方格纸中:
(1)请在方格纸上建立平面直角坐标系,使,并求出点坐标;
(2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形;
(3)计算的面积.
24、如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),BE⊥EF,且∠ABE+∠CEF=45°.
(1)求证:四边形ABCD是正方形;
(2)连接BD,交EF于点Q,求证:DQ BC=CE DF.
25、问题情境:如图1所示,在△ABC中,D、E分别是AB、AC上的点,DEBC,在图1中将ADE绕A点顺时针旋转一定角度,得到图2,然后将BD、CE分别延长至M、N,使DM=BD,EN=CE,得到图3,请解答下列问题:
(1)猜想证明:若AB=AC,请探究下列数量关系:
①在图2中,BD与CE的数量关系是_________.
②在图3中,猜想∠MAN与∠BAC的数量关系,并证明你的猜想;
(2)拓展应用:其他条件不变,若AB=AC,按上述操作方法,得到图4,请你继续探究:∠MAN与∠BAC的数量关系?AM与AN的数量关系?直接写出你的猜想.
一、选择题(每小题3分,共30分).
1、若,则等于( )
A. B. C. D.
2、如图,由下列条件不能判定△ABC与△ADE相似的是( )
A. B.∠B=∠ADE C. D.∠C=∠AED
3、如图,△ABC∽△ACP,若∠A=75°,∠APC=65°,则∠B的大小为( )
A.40° B.50° C.65° D.75°
4、如图,∠ACB=∠ADC=90°,BC=a,AC=b,AD=c,要使⊿ABC∽⊿CAD,只要CD等于( )
A. B. C. D.
5、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面直径为1.2米,桌面离地面1米.若灯泡离地面3 米,则地面上阴影部分的面积为( )
A.0..36π米2 B. 0.81π米2 C.2π米2 D.3. 24π米2
6、如图,在△ABC中,DE∥AB,且,则的值为( )
A. B. C. D.
7、如图,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA:OA1=1:3,则五边形ABCDE和五边形A1B1C1D1E1的面积比是( )
A.1:2 B.1:3 C.1:4 D.1:9
8、如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,若EF:AF=2:5,则为( )
A.2:5 B.4:25 C.4:31 D.4:35
9、如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A. B. C.1 D.1
10、如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为,,,.动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.作于点G,则运动过程中,AG的最大值为( )
A. B. C. D.8
二、填空题(每小题3分,共18分).
11、两个相似三角形的面积比为4:9,那么它们对应中线的比为 .
12、如图,△ADE~△ABC,AD=3,AE=4,BE=5,CA的长为 .
13、如图是一种贝壳的俯视图,点分线段近似于黄金分割.已知=10,则的长约为 .(结果精确到0.1)
14、如图,已知△ABC中,DE∥BC,连接BE,△ADE的面积是△BDE面积的,则= .
15、如图,正方形OEFG和正方形ABCD是位似图形,且点F与点C是一对对应点,点F的坐标是(1,1),点C的坐标是(4,2),则它们的位似中心的坐标是 .
16、如图,是的中位线,F为中点,连接并延长交于点G,若,则________.
三、解答题(共9小题,共72分).
17、已知:a:b:c=2:3:5(1)求代数式的值;(2)如果3a﹣b+c=24,求a,b,c的值.
18、如图,点C,D在线段AB上,且△PCD是等边三角形,AC=1,PC=2,BD=4.求证: △ACP∽△PDB.
19、为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面1.6米,标杆高为3.2米,且BC=2米,CD=6米,求树ED的高.
20、如图,AD是△ABC的中线,E是AD上一点,AE:AD=1:4,BE的延长线交AC于F,求AF:CF的值.
21、如图,在□ABCD中,E是 BC 边上一点,且 BE=EC,BD和AE 相交于F点.
(1)求△BEF 的周长与△AFD 的周长之比;
(2)若△BEF 的面积S△BEF=6 cm ,求△AFD 的面积.
22、小明放学回家途经一个小广场,广场的中央有一个羽毛球场地,场地的周围是片平坦的草坪,同时与羽毛球网在同一平面内有两个一样高的路灯,小明想测量路灯的高度AB,但是他没有带任何测量工具.于是,小明调整自己的步伐,尽量使得每一步步长相同,小明测出离路灯较近的网杆在路灯AB下的影长DF为2步,离路灯较远的网杆在路灯AB下的影长EC为5步,回家后小明上网查资料得到羽毛球网杆高DM=NE=1.55米,网长MN=61米,同时测得1步≈1米,求路灯的高度(结果保留一位小数).
23、如图,在方格纸中:
(1)请在方格纸上建立平面直角坐标系,使,并求出点坐标;
(2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形;
(3)计算的面积.
24、如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),BE⊥EF,且∠ABE+∠CEF=45°.
(1)求证:四边形ABCD是正方形;
(2)连接BD,交EF于点Q,求证:DQ BC=CE DF.
25、问题情境:如图1所示,在△ABC中,D、E分别是AB、AC上的点,DEBC,在图1中将ADE绕A点顺时针旋转一定角度,得到图2,然后将BD、CE分别延长至M、N,使DM=BD,EN=CE,得到图3,请解答下列问题:
(1)猜想证明:若AB=AC,请探究下列数量关系:
①在图2中,BD与CE的数量关系是_________.
②在图3中,猜想∠MAN与∠BAC的数量关系,并证明你的猜想;
(2)拓展应用:其他条件不变,若AB=AC,按上述操作方法,得到图4,请你继续探究:∠MAN与∠BAC的数量关系?AM与AN的数量关系?直接写出你的猜想.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
