人教版六年级下册数学3.3《圆柱的体积》课件(共20张PPT)
文档属性
| 名称 | 人教版六年级下册数学3.3《圆柱的体积》课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 581.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 11:00:37 | ||
图片预览




文档简介
(共20张PPT)
圆柱的体积
教学目标
1.经历推导圆柱的体积计算公式的过程,掌握圆柱的体积计算公式,体会转化思想在公式推导中的作用,培养空间观念。
2.能运用圆柱的体积计算公式求圆柱的体积,并解决相关的实际问题,培养应用意识。
3.在推导公式的过程中进一步培养动手操作能力,发展空间观念,
增强学习数学的兴趣。
教学重点:
掌握圆柱体积的计算公式,并应用公式解决问题。
教学难点:
建立圆柱与其转化后的长方体之间的对应关系。
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
底面积
底面积
长方体的体积= ×高
正方体的体积= ×高
复习:
之前学过哪些立体图形的体积?
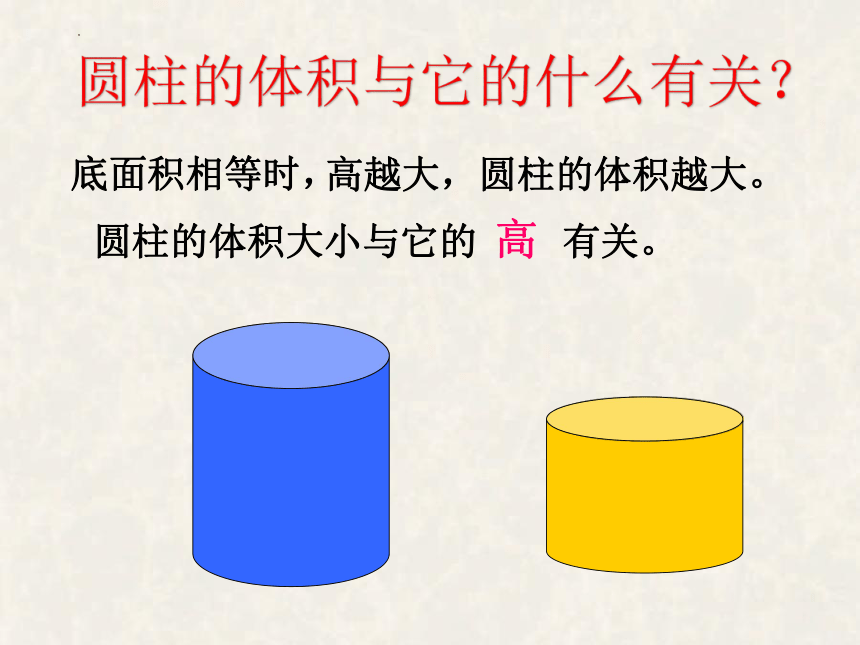
底面积相等时,
圆柱的体积大小与它的 有关。
高
高越大,圆柱的体积越大。
圆柱的体积与它的什么有关?
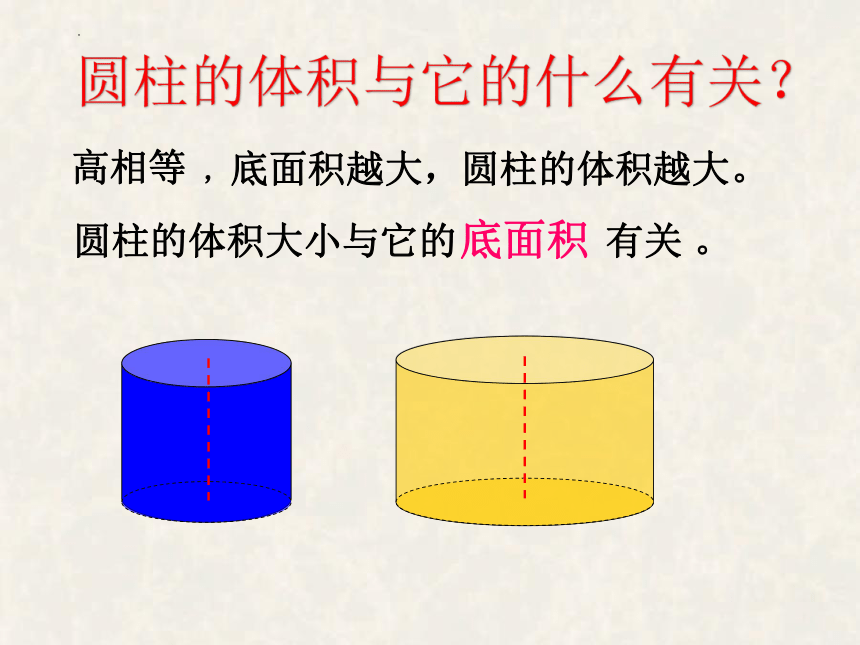
高相等
,底面积越大,圆柱的体积越大。
圆柱的体积大小与它的 有关 。
底面积
圆柱的体积与它的什么有关?
底面积、高
圆柱的体积大小,
与它的底面积和高的大小有关。
小结
圆柱体的体积=底面积×高
猜想:
圆柱的体积公式
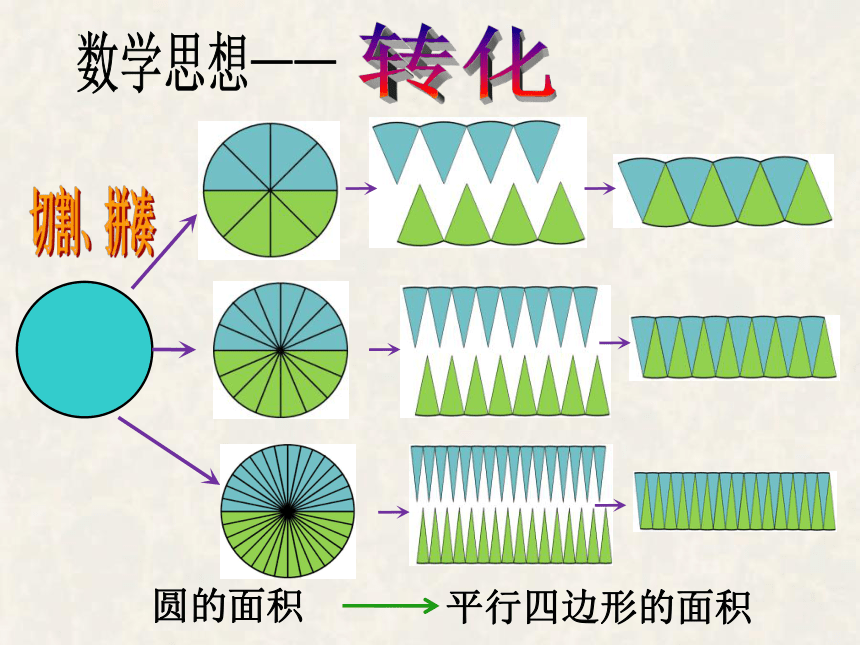
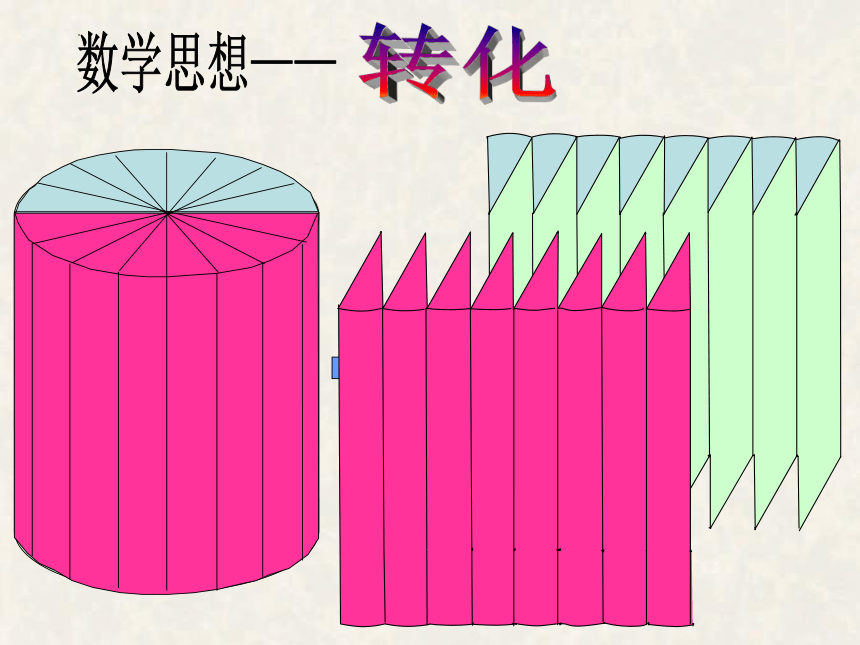
数学思想——
转化
圆的面积
平行四边形的面积
切割、拼凑
数学思想——
转化
将圆柱分的份数越多,拼成的立体图就越接近长方体
数学思想——
转化
同样的物体改变形状,
体积不变
圆柱的体积
长方体的体积
1.圆柱转化成长方体,什么变了,什么不变?
2.你能找出它们之间哪些相等的关系?
思考:
表面积变了,体积不变
3.圆柱的体积该如何计算?
高
底面积
πr
高
1.圆柱转化成长方体,什么变了,什么不变?
2.你能找出它们之间哪些相等的关系?
表面积变了,体积不变
长方体的体积
C÷2=πr
r
圆柱的体积
长
πr
宽
r
高
h
思考:
底面积
πr
高
底面积
Πr
高
C÷2=πr
r
3.圆柱的体积该如何计算?
思考:
=πr h
V=Sh
圆柱的体积
长
πr
宽
r
高
h
底面积
πr
= 底面积 × 高
长方体的体积
总结:
高
高
利用 的数学思想 ,将圆柱转化成 ,发现长方体的底面积与圆柱的 相等,长方体的高
等于圆柱的 ,因此得出圆柱的体积= 。
转化
长方体
底面积
高
底面积×高
它们都可以想成由形状、大小相等的平面图形,一层一层的叠加所形成的立体图形。
它们有什么共同的特点?
思考:
体积= 底面积×高
判断下列立体图形的体积能否用底面积乘高来计算?
如果可以的话,它们分别可以看做是哪些形状、大小相等的平面图形叠加组成的呢?
由形状、大小相等的三角形叠加而成
体积=底面积×高
由形状、大小相等的圆环叠加而成
体积=底面积×高
不是由形状、大小相等的圆叠加而成
练一练
一个圆柱体零件,底面半径是5厘米,高是10厘米,这个零件的体积是多少立方厘米?
S :5×5×3.14=78.5(平方厘米)
V :78.5× 10=785(立方厘米)
答:这个零件的体积是785立方厘米。
V=Sh
5CM
10CM
一个圆柱形容器的底面周长是18.84厘米,放入一个鸡蛋后水面上升2cm(水完全淹没鸡蛋),鸡蛋的体积是多少立方厘米?
拓展:
底面周长
半径
底面面积
上升的水的体积
鸡蛋的体积
1.我们学过的哪些立体图形的体积能用“体积=底面积×高”来表示呢?把你想到的图形写出来。
作业:
2.你想到的这些图形的表面积可以用“表面积=侧面积+ ”来表示。
3.下面这三个立体图形的体积能用底面积×高计算的请在括号里画“ “,不能的画“×”,说说你是怎么想的。
( )
( )
( )
谢谢观看
圆柱的体积
教学目标
1.经历推导圆柱的体积计算公式的过程,掌握圆柱的体积计算公式,体会转化思想在公式推导中的作用,培养空间观念。
2.能运用圆柱的体积计算公式求圆柱的体积,并解决相关的实际问题,培养应用意识。
3.在推导公式的过程中进一步培养动手操作能力,发展空间观念,
增强学习数学的兴趣。
教学重点:
掌握圆柱体积的计算公式,并应用公式解决问题。
教学难点:
建立圆柱与其转化后的长方体之间的对应关系。
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
底面积
底面积
长方体的体积= ×高
正方体的体积= ×高
复习:
之前学过哪些立体图形的体积?
底面积相等时,
圆柱的体积大小与它的 有关。
高
高越大,圆柱的体积越大。
圆柱的体积与它的什么有关?
高相等
,底面积越大,圆柱的体积越大。
圆柱的体积大小与它的 有关 。
底面积
圆柱的体积与它的什么有关?
底面积、高
圆柱的体积大小,
与它的底面积和高的大小有关。
小结
圆柱体的体积=底面积×高
猜想:
圆柱的体积公式
数学思想——
转化
圆的面积
平行四边形的面积
切割、拼凑
数学思想——
转化
将圆柱分的份数越多,拼成的立体图就越接近长方体
数学思想——
转化
同样的物体改变形状,
体积不变
圆柱的体积
长方体的体积
1.圆柱转化成长方体,什么变了,什么不变?
2.你能找出它们之间哪些相等的关系?
思考:
表面积变了,体积不变
3.圆柱的体积该如何计算?
高
底面积
πr
高
1.圆柱转化成长方体,什么变了,什么不变?
2.你能找出它们之间哪些相等的关系?
表面积变了,体积不变
长方体的体积
C÷2=πr
r
圆柱的体积
长
πr
宽
r
高
h
思考:
底面积
πr
高
底面积
Πr
高
C÷2=πr
r
3.圆柱的体积该如何计算?
思考:
=πr h
V=Sh
圆柱的体积
长
πr
宽
r
高
h
底面积
πr
= 底面积 × 高
长方体的体积
总结:
高
高
利用 的数学思想 ,将圆柱转化成 ,发现长方体的底面积与圆柱的 相等,长方体的高
等于圆柱的 ,因此得出圆柱的体积= 。
转化
长方体
底面积
高
底面积×高
它们都可以想成由形状、大小相等的平面图形,一层一层的叠加所形成的立体图形。
它们有什么共同的特点?
思考:
体积= 底面积×高
判断下列立体图形的体积能否用底面积乘高来计算?
如果可以的话,它们分别可以看做是哪些形状、大小相等的平面图形叠加组成的呢?
由形状、大小相等的三角形叠加而成
体积=底面积×高
由形状、大小相等的圆环叠加而成
体积=底面积×高
不是由形状、大小相等的圆叠加而成
练一练
一个圆柱体零件,底面半径是5厘米,高是10厘米,这个零件的体积是多少立方厘米?
S :5×5×3.14=78.5(平方厘米)
V :78.5× 10=785(立方厘米)
答:这个零件的体积是785立方厘米。
V=Sh
5CM
10CM
一个圆柱形容器的底面周长是18.84厘米,放入一个鸡蛋后水面上升2cm(水完全淹没鸡蛋),鸡蛋的体积是多少立方厘米?
拓展:
底面周长
半径
底面面积
上升的水的体积
鸡蛋的体积
1.我们学过的哪些立体图形的体积能用“体积=底面积×高”来表示呢?把你想到的图形写出来。
作业:
2.你想到的这些图形的表面积可以用“表面积=侧面积+ ”来表示。
3.下面这三个立体图形的体积能用底面积×高计算的请在括号里画“ “,不能的画“×”,说说你是怎么想的。
( )
( )
( )
谢谢观看
