1.5三角函数的应用 北师大版初中数学九年级下册同步练习(含解析)
文档属性
| 名称 | 1.5三角函数的应用 北师大版初中数学九年级下册同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 642.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.5三角函数的应用北师大版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为,缆车速度为每分钟米,从山脚下到达山顶缆车需要分钟,则山的高度为( )
A. B. C. D.
2.某车库出口安装的栏杆如图所示,点是栏杆转动的支点,点是栏杆两段的联结点.当车辆经过时,栏杆最多只能升起到如图所示的位置,其示意图如图所示栏杆宽度忽略不计,其中,,,米,米,那么适合该地下车库的车辆限高标志牌为参考数据:,,( )
A. B. C. D.
3.如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点,测得,米,,则这棵树的高约为参考数据:,,( )
A. 米 B. 米 C. 米 D. 米
4.如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成角,房屋朝南的窗子高,要在窗子外面上方安装水平挡光板,使午间光线不能直接射入室内,那么挡光板的宽度应为
( )
A. B. C. D.
5.如图,一块矩形木板斜靠在墙边在同一平面内,已知,,,则点到的距离等于
( )
A. B. C. D.
6.小甬和小真两位同学来到体育馆前一个半圆形公益广告牌前,广告牌如图所示,两位同学认为如果要测得广告牌的半径,按以下方案获取数据后即可求得:他们先测得广告牌的影长为米,然后小甬让小真站立,测得小真的影长为米,已知小真同学身高为米,那么广告牌的半径是( )
A. 米 B. 米 C. 米 D. 米
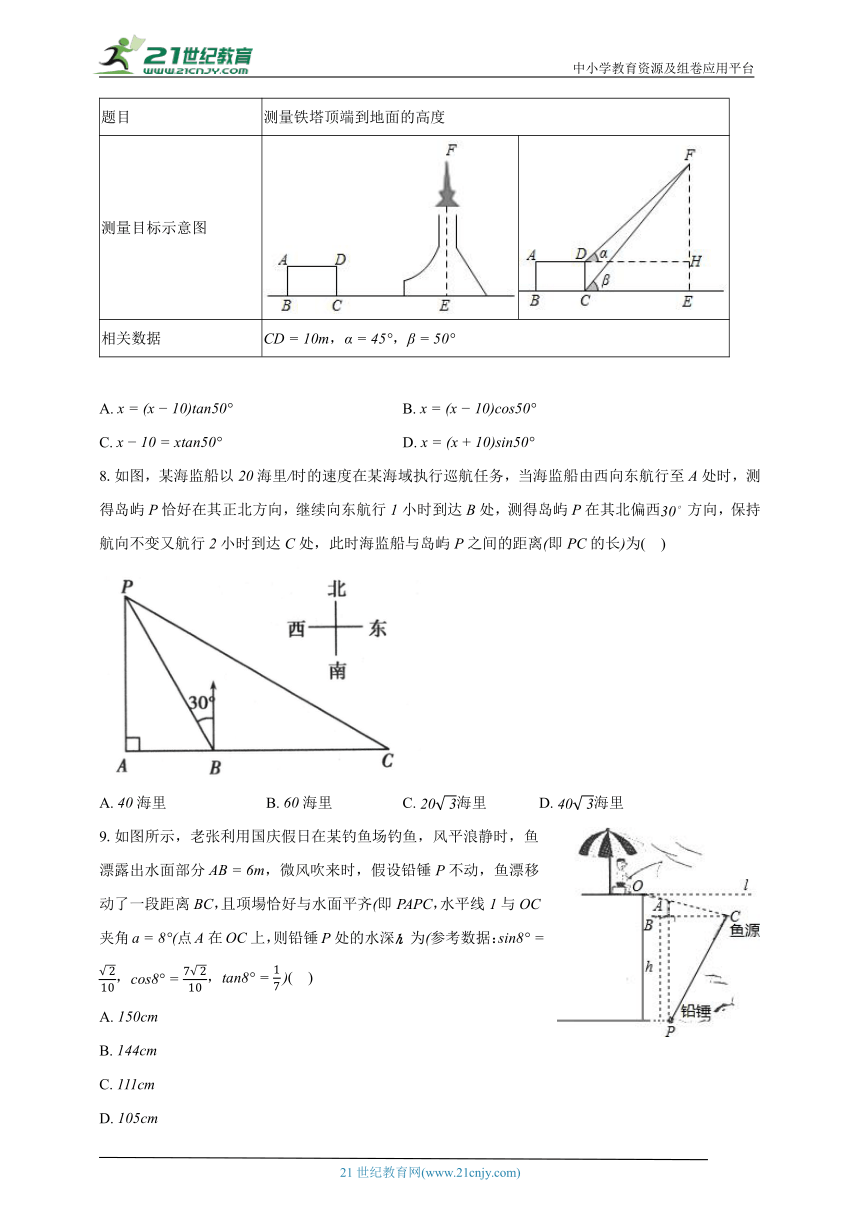
7.下表是小红填写的实践活动报告的部分内容:设铁塔顶端到地面的高度为,根据以上条件,可以列出的方程为( )
题目 测量铁塔顶端到地面的高度
测量目标示意图
相关数据 ,,
A. B.
C. D.
8.如图,某海监船以海里时的速度在某海域执行巡航任务,当海监船由西向东航行至处时,测得岛屿恰好在其正北方向,继续向东航行小时到达处,测得岛屿在其北偏西方向,保持航向不变又航行小时到达处,此时海监船与岛屿之间的距离即的长为( )
A. 海里 B. 海里 C. 海里 D. 海里
9.如图所示,老张利用国庆假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分,微风吹来时,假设铅锤不动,鱼漂移动了一段距离,且项場恰好与水面平齐即,水平线与夹角点在上,则铅锤处的水深为参考数据:,,( )
A.
B.
C.
D.
10.为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度或坡比:的山坡上发现有一棵古树测得古树底端到山脚点的距离米,在距山脚点水平距离米的点处,测得古树顶端的仰角古树与山坡的剖面、点在同一平面上,古树与直线垂直,则古树的高度约为( )
参考数据:,,
A. 米 B. 米 C. 米 D. 米
11.如图,某同学用圆规画一个半径为的圆,测得此时,为了画一个半径更大的圆,固定端不动,将端向左移至处,此时测得,则的长为.( )
A. B. C. D.
12. 某地、两市被大山阻隔,若要从市到市,只能沿着公路先从市到市,再由市到市.现计划开凿隧道使,两地直线贯通.下表是九年级兴趣小组设计的实践活动报告的部分内容:结果精确到,参考数据:,
题目 隧道开通后缩短的路程
测量目标示意图
相关数据 ,,
通过计算隧道开通后缩短的路程是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
13.已知不等臂跷跷板长为米,当的一端点碰到地面时如图,与地面的夹角为,当的另一端点碰到地面时如图,与地面的夹角的正弦值为,那么跷跷板的支撑点到地面的距离 米
14.如图是一台手机支架的侧面示意图,,可分别绕点,转动,测量知,当,转动到,时,点到的距离为 结果保留小数点后一位,参考数据:,.
15.如图,某小区两幢楼房的间距为,在某一时刻太阳光线与水平线的夹角为若两幢楼高均为,则楼甲的影子落在楼乙上的高度为
16.如图,在离水面高度为米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为,此人以每秒米收绳.问:未开始收绳子的时候,图中绳子的长度是______米;收绳秒后船向岸边移动了______米.结果保留根号
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
某兴趣小组为了测量大楼的高度,先沿着斜坡走了米到达坡顶点处,然后在点处测得大楼顶点的仰角为,已知斜坡的坡度为:,点到大楼的距离为米,求大楼的高度.
参考数据:,,
18.本小题分
如图,一座钢结构桥梁的框架是,水平横梁长米,中柱高米,其中是的中点,且.
求的值;
现需要加装支架、,其中点在上,,且,垂足为点,求支架的长.
19.本小题分
某地下车库出口处安装了“两段式栏杆”,如图所示,点是栏杆转动的支点,点是栏杆两段的联结点.当车辆经过时,栏杆最多只能升起到如图所示的位置,其示意图如图所示栏杆宽度忽略不计,其中,,,米,那么适合该地下车库的车辆限高标志牌为多少米?结果精确到参考数据:,,
20.本小题分
如图,山顶上有一个信号塔,已知信号塔高米,在山脚下点处测得塔底的仰角,塔顶的仰角,求山高点,,在同一条竖直线上.
参考数据:,,
21.本小题分
如图,某旅游景区为方便游客,修建了一条东西走向的木栈道,栈道与景区道路平行.在处测得栈道一端位于北偏西方向,在处测得栈道另一端位于北偏西方向.已知,,求木栈道的长度结果保留整数.
参考数据:,,,,,
22.本小题分
图是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线上,转到地面的距离小亮在荡秋千过程中,当秋千摆动到最高点时,测得点到的距离,点到地面的距离;当他从处摆动到处时,有.
求到的距离;
求到地面的距离.
23.本小题分
成都“”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶处测得塔处的仰角为,塔底部处的俯角为已知建筑物的高约为米,请计算观景台的高的值.
结果精确到米;参考数据:,,
24.本小题分
如图是一辆吊车的实物图,图是其工作示意图,其转动点离地面的高度为,是可以伸缩的起重臂,当长度为,张角为时,求起重臂顶点离地面的高度结果保留小数点后一位参考数据:,,
25.本小题分
如图,水库大坝的横截面是梯形,其中,坝顶,坡长,坡底,.
求的度数结果精确到;
如果坝长,那么建筑这个大坝共需多少土石料?结果精确到
答案和解析
1.【答案】
【解析】解:如图,作,垂足为.
在中,,
,米,
,
.
故选:.
作,垂足为,在中,利用三角函数解答即可.
本题考查了解直角三角形的应用,找到直角三角形并熟悉三角函数的运算是解题的关键.
2.【答案】
【解析】【分析】
本题主要考查解直角三角形的应用,解题的关键是结合题意构建直角三角形,并熟练掌握正弦函数的概念.
延长、,交于点,根据,知,由知,根据,米,求出的长,继而可得的值,从而得出答案.
【解答】
解:如图,延长、,交于点,
,,
,即,
,
,
在中,
,米,
米,
则米,
故选:.
3.【答案】
【解析】【分析】
本题考查解直角三角形的应用,勾股定理的应用等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于常考题型.
如图,作于设,构建方程即可解决问题.
【解答】
解:如图,作于.
,,
设,
,
,
,
,
,
故选:.
4.【答案】
【解析】【分析】
此题主要考查了解直角三角形的应用,正确掌握锐角三角函数关系是解题关键.根据题意得出:,,再利用锐角三角函数关系得出答案.
【解答】
解:如图所示:
由题意可得:,,,
.
故选D.
5.【答案】
【解析】略
6.【答案】
【解析】解:如图,设圆心为,是半径,点是光线与半圆的切点,延长交于,过点作交光线于,设米.
由题意米,
,
米,
,都是切线,
,
在中,,
,,
∽,
,
,
,
故选:.
如图,设圆心为,是半径,点是光线与半圆的切点,延长交于,过点作交的延长线于,设米.求出,再利用相似三角形的性质即可解决问题.
本题考查相似三角形的判定和性质等知识,解题的关键是理解题意,学会添加常用辅助线,构造相似三角形解决问题.
7.【答案】
【解析】解:过作于,
则四边形是矩形,
,,
,
,
,
,
,
,
故选:.
过作于,则四边形是矩形,根据矩形的性质得到,,求得,得到,根据三角函数的定义列方程即可得到结论.
本题考查了解直角三角形的应用,由实际问题抽象出一元一次方程,正确的识别图形是解题的关键.
8.【答案】
【解析】【分析】本题考查解直角三角形的应用方向角问题,解题的关键是证明,推出,可得,求出即可解决问题。
【解答】解:在中,
,
,
由题意知,
,
,
,
,,
,
海里.
故选D.
9.【答案】
【解析】解:,,
在中,,
,
根据题意,得,
.
故选:.
在中,已知,,根据三角函数就可以求出的长;在直角中,根据已知条件,利用勾股定理就可以求出水深.
本题考查了学生运用三角函数知识解决实际问题的能力,又让学生感受到生活处处有数学,数学在生产生活中有着广泛的作用.
10.【答案】
【解析】【分析】本题考查解直角三角形的应用仰角俯角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
如图,根据已知条件得到:,设,,根据勾股定理得到,求得,,得到,根据三角函数的定义即可得到结论.
【解答】解:如图,:,
设,,
,
,
,,
,
,
,
,
,
,
答:古树的高度约为米,
故选:.
11.【答案】
【解析】【分析】
此题考查了解直角三角形的应用,主要是三角函数的概念及运算,关键把实际问题转化为数学问题加以计算.
根据是等腰直角三角形,利用三角函数即可求得的长,过作于点,在直角中利用三角函数求得的长,则,然后根据即可求解.
【解答】
解:在等腰直角中,,则,
如图,过作于点,
,
则.
则,
故BB.
故选:.
12.【答案】
【解析】【分析】
此题主要考查了解直角三角形的应用,正确掌握边角关系是解题关键.
直接利用锐角三角函数关系分别得出,,,的长进而得出答案.
【解答】
解:由题意可得:,
解得:,
,
,
,
则,
则,
,
故隧道开通后缩短的路程是:.
故选:.
13.【答案】
【解析】【分析】
此题主要考查了解直角三角形的应用,正确用未知数表示出的长是解题关键.
利用锐角三角函数关系以及特殊角的三角函数关系表示出的长,进而求出即可.
【解答】
解:设米,
当的一端点碰到地面时,与地面的夹角为,
米,
当的另一端点碰到地面时,与地面的夹角的正弦值为,
米,
则米,
解得米.
故答案为.
14.【答案】
【解析】解:如图,过点,分别作的垂线,垂足为点,过点作 ,垂足为点.
在中,,,
,.
在中,,
.
又,
,
即点到的距离约为.
15.【答案】
【解析】【分析】
本题主要考查了三角函数定义的应用在中,根据三角函数可求的长,,即可解答.
【解答】
解:如图:作,垂足为,可得,矩形,
,
,
.
.
故答案为:.
16.【答案】
【解析】解:如图,在中,,
米;
未收绳时米
收绳秒后,绳子缩短了米,只有米,即米,
在中,由米,米,
根据勾股定理得船到河岸的距离米.
故移动距离米,
故答案为
利用的正弦值可得未开始收绳子的时候,图中绳子的长度;
利用的余弦值可得未开始收绳子的时候长,易得收绳后长,利用勾股定理可得收绳后长,让未收绳时长减去收绳后长即为船向岸边移动的距离.
考查解直角三角形在实际生活中的应用,用到的知识点为:知道对边求斜边,可用正弦值,用除法;知道对边,求邻边,用除法,用正切值.
17.【答案】解:如图,过点作于点,于点,
,
易得四边形是矩形,
,,
在中,:::,
设,,
根据勾股定理,得,
,
解得,
,
,
,
在中,,
米.
答:大楼的高度约为米.
【解析】本题考查了解直角三角形的应用仰角俯角问题和坡度坡角问题,解决本题的关键是掌握仰角俯角和坡度坡角定义.
过点作于点,于点,可得四边形是矩形,根据斜坡的坡度为:,设,,利用勾股定理可得的值,再根据锐角三角函数即可进一步求大楼的高度.
18.【答案】解:在中,,,
,
.
,,
,
,
又,
,
又,
,
,
,,
,
在中,.
【解析】在中,利用勾股定理求出,再根据计算即可;
由,,可得,求出、即可利用勾股定理解决问题;
本题考查解直角三角形的应用,相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
19.【答案】解:如图,过点作的平行线,过点作于,
则,
,
,,
在中,,,米,
米,
米,
米
答:适合该地下车库的车辆限高标志牌为米.
【解析】本题考查了解直角三角形在实际中的应用,难度适中.关键是通过作辅助线,构造直角三角形,把实际问题转化为数学问题加以计算.过点作的平行线,过点作于,则,先求出,则,然后在中,利用正弦函数的定义得出,则栏杆段距离地面的高度为:,代入数值计算即可.
20.【答案】解:由题意,在中,,
,
,
在中,,
,
,
,
,
米,
米,
答:山高约为米.
【解析】本题考查了解直角三角形的应用仰角俯角问题,注意方程思想与数形结合思想的应用.
根据锐角三角函数的定义得出,,利用,求出的长,即可求出的长.
21.【答案】解:过作于,交的延长线于,
则,
,
四边形是矩形,
,,
在中,,,
,,
,
在中,,,
,
,
答:木栈道的长度约为.
【解析】本题考查解直角三角形方向角问题,解题的关键是学会添加常用辅助线.构造直角三角形解决问题,属于中考常考题型.
过作于,交的延长线于,于是得到,推出四边形是矩形,得到,,解直角三角形即可得到结论.
22.【答案】解:如图,作,垂足为
,
;
在中,;
图又,
,
;
在和中,,
≌;
,
且,,
;
,
,
即到的距离是.
由知:≌,
,
作,垂足为.
,
,
,
即到地面的距离是.
【解析】本题主要考查了三角形全等的判定与性质的应用熟练掌握定理是解题的关键.
作,垂足为,利用三角形全等得到≌,根据三角形全等的性质得到,可以求出结果;
由知:≌,根据三角形全等的性质得到:, 作,垂足为,得到,可以求出结果.
23.【答案】解:过点作于点,
根据题意可得四边形是矩形,
,米,
在中,
,
,
,
在中,,
,
米.
答:观景台的高的值约为米.
【解析】本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
过点作于点,根据题意可得四边形是矩形,,,再根据锐角三角函数可得的长,进而可得的值.
24.【答案】解:过点作于过点作于.
矩形,,,.
,.
在中,.
,
点离地面的高度为.
【解析】作于,于,则四边形为矩形,得出,,求出,在中利用正弦可计算出,然后计算即可.
本题考查了解直角三角形的应用:先将实际问题抽象为数学问题,构造出直角三角形转化为解直角三角形问题,然后利用勾股定理和三角函数的定义进行计算.
25.【答案】解:作于点,于点,则.
梯形中,,
,
.
,
在直角中,,
则,则;
,
则建筑这个大坝共需土石料
答:建筑这个大坝共需土石料.
【解析】作于点,于点,在直角中,求得的长,即的长,在直角中即可求得的正切值,即可求解;
求得截面积,然后乘以即可求解.
本题考查了解直角三角形的应用,以及三角函数,解题的基本依据是转化为解直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.5三角函数的应用北师大版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为,缆车速度为每分钟米,从山脚下到达山顶缆车需要分钟,则山的高度为( )
A. B. C. D.
2.某车库出口安装的栏杆如图所示,点是栏杆转动的支点,点是栏杆两段的联结点.当车辆经过时,栏杆最多只能升起到如图所示的位置,其示意图如图所示栏杆宽度忽略不计,其中,,,米,米,那么适合该地下车库的车辆限高标志牌为参考数据:,,( )
A. B. C. D.
3.如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点,测得,米,,则这棵树的高约为参考数据:,,( )
A. 米 B. 米 C. 米 D. 米
4.如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成角,房屋朝南的窗子高,要在窗子外面上方安装水平挡光板,使午间光线不能直接射入室内,那么挡光板的宽度应为
( )
A. B. C. D.
5.如图,一块矩形木板斜靠在墙边在同一平面内,已知,,,则点到的距离等于
( )
A. B. C. D.
6.小甬和小真两位同学来到体育馆前一个半圆形公益广告牌前,广告牌如图所示,两位同学认为如果要测得广告牌的半径,按以下方案获取数据后即可求得:他们先测得广告牌的影长为米,然后小甬让小真站立,测得小真的影长为米,已知小真同学身高为米,那么广告牌的半径是( )
A. 米 B. 米 C. 米 D. 米
7.下表是小红填写的实践活动报告的部分内容:设铁塔顶端到地面的高度为,根据以上条件,可以列出的方程为( )
题目 测量铁塔顶端到地面的高度
测量目标示意图
相关数据 ,,
A. B.
C. D.
8.如图,某海监船以海里时的速度在某海域执行巡航任务,当海监船由西向东航行至处时,测得岛屿恰好在其正北方向,继续向东航行小时到达处,测得岛屿在其北偏西方向,保持航向不变又航行小时到达处,此时海监船与岛屿之间的距离即的长为( )
A. 海里 B. 海里 C. 海里 D. 海里
9.如图所示,老张利用国庆假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分,微风吹来时,假设铅锤不动,鱼漂移动了一段距离,且项場恰好与水面平齐即,水平线与夹角点在上,则铅锤处的水深为参考数据:,,( )
A.
B.
C.
D.
10.为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度或坡比:的山坡上发现有一棵古树测得古树底端到山脚点的距离米,在距山脚点水平距离米的点处,测得古树顶端的仰角古树与山坡的剖面、点在同一平面上,古树与直线垂直,则古树的高度约为( )
参考数据:,,
A. 米 B. 米 C. 米 D. 米
11.如图,某同学用圆规画一个半径为的圆,测得此时,为了画一个半径更大的圆,固定端不动,将端向左移至处,此时测得,则的长为.( )
A. B. C. D.
12. 某地、两市被大山阻隔,若要从市到市,只能沿着公路先从市到市,再由市到市.现计划开凿隧道使,两地直线贯通.下表是九年级兴趣小组设计的实践活动报告的部分内容:结果精确到,参考数据:,
题目 隧道开通后缩短的路程
测量目标示意图
相关数据 ,,
通过计算隧道开通后缩短的路程是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
13.已知不等臂跷跷板长为米,当的一端点碰到地面时如图,与地面的夹角为,当的另一端点碰到地面时如图,与地面的夹角的正弦值为,那么跷跷板的支撑点到地面的距离 米
14.如图是一台手机支架的侧面示意图,,可分别绕点,转动,测量知,当,转动到,时,点到的距离为 结果保留小数点后一位,参考数据:,.
15.如图,某小区两幢楼房的间距为,在某一时刻太阳光线与水平线的夹角为若两幢楼高均为,则楼甲的影子落在楼乙上的高度为
16.如图,在离水面高度为米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为,此人以每秒米收绳.问:未开始收绳子的时候,图中绳子的长度是______米;收绳秒后船向岸边移动了______米.结果保留根号
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
某兴趣小组为了测量大楼的高度,先沿着斜坡走了米到达坡顶点处,然后在点处测得大楼顶点的仰角为,已知斜坡的坡度为:,点到大楼的距离为米,求大楼的高度.
参考数据:,,
18.本小题分
如图,一座钢结构桥梁的框架是,水平横梁长米,中柱高米,其中是的中点,且.
求的值;
现需要加装支架、,其中点在上,,且,垂足为点,求支架的长.
19.本小题分
某地下车库出口处安装了“两段式栏杆”,如图所示,点是栏杆转动的支点,点是栏杆两段的联结点.当车辆经过时,栏杆最多只能升起到如图所示的位置,其示意图如图所示栏杆宽度忽略不计,其中,,,米,那么适合该地下车库的车辆限高标志牌为多少米?结果精确到参考数据:,,
20.本小题分
如图,山顶上有一个信号塔,已知信号塔高米,在山脚下点处测得塔底的仰角,塔顶的仰角,求山高点,,在同一条竖直线上.
参考数据:,,
21.本小题分
如图,某旅游景区为方便游客,修建了一条东西走向的木栈道,栈道与景区道路平行.在处测得栈道一端位于北偏西方向,在处测得栈道另一端位于北偏西方向.已知,,求木栈道的长度结果保留整数.
参考数据:,,,,,
22.本小题分
图是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线上,转到地面的距离小亮在荡秋千过程中,当秋千摆动到最高点时,测得点到的距离,点到地面的距离;当他从处摆动到处时,有.
求到的距离;
求到地面的距离.
23.本小题分
成都“”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶处测得塔处的仰角为,塔底部处的俯角为已知建筑物的高约为米,请计算观景台的高的值.
结果精确到米;参考数据:,,
24.本小题分
如图是一辆吊车的实物图,图是其工作示意图,其转动点离地面的高度为,是可以伸缩的起重臂,当长度为,张角为时,求起重臂顶点离地面的高度结果保留小数点后一位参考数据:,,
25.本小题分
如图,水库大坝的横截面是梯形,其中,坝顶,坡长,坡底,.
求的度数结果精确到;
如果坝长,那么建筑这个大坝共需多少土石料?结果精确到
答案和解析
1.【答案】
【解析】解:如图,作,垂足为.
在中,,
,米,
,
.
故选:.
作,垂足为,在中,利用三角函数解答即可.
本题考查了解直角三角形的应用,找到直角三角形并熟悉三角函数的运算是解题的关键.
2.【答案】
【解析】【分析】
本题主要考查解直角三角形的应用,解题的关键是结合题意构建直角三角形,并熟练掌握正弦函数的概念.
延长、,交于点,根据,知,由知,根据,米,求出的长,继而可得的值,从而得出答案.
【解答】
解:如图,延长、,交于点,
,,
,即,
,
,
在中,
,米,
米,
则米,
故选:.
3.【答案】
【解析】【分析】
本题考查解直角三角形的应用,勾股定理的应用等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于常考题型.
如图,作于设,构建方程即可解决问题.
【解答】
解:如图,作于.
,,
设,
,
,
,
,
,
故选:.
4.【答案】
【解析】【分析】
此题主要考查了解直角三角形的应用,正确掌握锐角三角函数关系是解题关键.根据题意得出:,,再利用锐角三角函数关系得出答案.
【解答】
解:如图所示:
由题意可得:,,,
.
故选D.
5.【答案】
【解析】略
6.【答案】
【解析】解:如图,设圆心为,是半径,点是光线与半圆的切点,延长交于,过点作交光线于,设米.
由题意米,
,
米,
,都是切线,
,
在中,,
,,
∽,
,
,
,
故选:.
如图,设圆心为,是半径,点是光线与半圆的切点,延长交于,过点作交的延长线于,设米.求出,再利用相似三角形的性质即可解决问题.
本题考查相似三角形的判定和性质等知识,解题的关键是理解题意,学会添加常用辅助线,构造相似三角形解决问题.
7.【答案】
【解析】解:过作于,
则四边形是矩形,
,,
,
,
,
,
,
,
故选:.
过作于,则四边形是矩形,根据矩形的性质得到,,求得,得到,根据三角函数的定义列方程即可得到结论.
本题考查了解直角三角形的应用,由实际问题抽象出一元一次方程,正确的识别图形是解题的关键.
8.【答案】
【解析】【分析】本题考查解直角三角形的应用方向角问题,解题的关键是证明,推出,可得,求出即可解决问题。
【解答】解:在中,
,
,
由题意知,
,
,
,
,,
,
海里.
故选D.
9.【答案】
【解析】解:,,
在中,,
,
根据题意,得,
.
故选:.
在中,已知,,根据三角函数就可以求出的长;在直角中,根据已知条件,利用勾股定理就可以求出水深.
本题考查了学生运用三角函数知识解决实际问题的能力,又让学生感受到生活处处有数学,数学在生产生活中有着广泛的作用.
10.【答案】
【解析】【分析】本题考查解直角三角形的应用仰角俯角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
如图,根据已知条件得到:,设,,根据勾股定理得到,求得,,得到,根据三角函数的定义即可得到结论.
【解答】解:如图,:,
设,,
,
,
,,
,
,
,
,
,
,
答:古树的高度约为米,
故选:.
11.【答案】
【解析】【分析】
此题考查了解直角三角形的应用,主要是三角函数的概念及运算,关键把实际问题转化为数学问题加以计算.
根据是等腰直角三角形,利用三角函数即可求得的长,过作于点,在直角中利用三角函数求得的长,则,然后根据即可求解.
【解答】
解:在等腰直角中,,则,
如图,过作于点,
,
则.
则,
故BB.
故选:.
12.【答案】
【解析】【分析】
此题主要考查了解直角三角形的应用,正确掌握边角关系是解题关键.
直接利用锐角三角函数关系分别得出,,,的长进而得出答案.
【解答】
解:由题意可得:,
解得:,
,
,
,
则,
则,
,
故隧道开通后缩短的路程是:.
故选:.
13.【答案】
【解析】【分析】
此题主要考查了解直角三角形的应用,正确用未知数表示出的长是解题关键.
利用锐角三角函数关系以及特殊角的三角函数关系表示出的长,进而求出即可.
【解答】
解:设米,
当的一端点碰到地面时,与地面的夹角为,
米,
当的另一端点碰到地面时,与地面的夹角的正弦值为,
米,
则米,
解得米.
故答案为.
14.【答案】
【解析】解:如图,过点,分别作的垂线,垂足为点,过点作 ,垂足为点.
在中,,,
,.
在中,,
.
又,
,
即点到的距离约为.
15.【答案】
【解析】【分析】
本题主要考查了三角函数定义的应用在中,根据三角函数可求的长,,即可解答.
【解答】
解:如图:作,垂足为,可得,矩形,
,
,
.
.
故答案为:.
16.【答案】
【解析】解:如图,在中,,
米;
未收绳时米
收绳秒后,绳子缩短了米,只有米,即米,
在中,由米,米,
根据勾股定理得船到河岸的距离米.
故移动距离米,
故答案为
利用的正弦值可得未开始收绳子的时候,图中绳子的长度;
利用的余弦值可得未开始收绳子的时候长,易得收绳后长,利用勾股定理可得收绳后长,让未收绳时长减去收绳后长即为船向岸边移动的距离.
考查解直角三角形在实际生活中的应用,用到的知识点为:知道对边求斜边,可用正弦值,用除法;知道对边,求邻边,用除法,用正切值.
17.【答案】解:如图,过点作于点,于点,
,
易得四边形是矩形,
,,
在中,:::,
设,,
根据勾股定理,得,
,
解得,
,
,
,
在中,,
米.
答:大楼的高度约为米.
【解析】本题考查了解直角三角形的应用仰角俯角问题和坡度坡角问题,解决本题的关键是掌握仰角俯角和坡度坡角定义.
过点作于点,于点,可得四边形是矩形,根据斜坡的坡度为:,设,,利用勾股定理可得的值,再根据锐角三角函数即可进一步求大楼的高度.
18.【答案】解:在中,,,
,
.
,,
,
,
又,
,
又,
,
,
,,
,
在中,.
【解析】在中,利用勾股定理求出,再根据计算即可;
由,,可得,求出、即可利用勾股定理解决问题;
本题考查解直角三角形的应用,相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
19.【答案】解:如图,过点作的平行线,过点作于,
则,
,
,,
在中,,,米,
米,
米,
米
答:适合该地下车库的车辆限高标志牌为米.
【解析】本题考查了解直角三角形在实际中的应用,难度适中.关键是通过作辅助线,构造直角三角形,把实际问题转化为数学问题加以计算.过点作的平行线,过点作于,则,先求出,则,然后在中,利用正弦函数的定义得出,则栏杆段距离地面的高度为:,代入数值计算即可.
20.【答案】解:由题意,在中,,
,
,
在中,,
,
,
,
,
米,
米,
答:山高约为米.
【解析】本题考查了解直角三角形的应用仰角俯角问题,注意方程思想与数形结合思想的应用.
根据锐角三角函数的定义得出,,利用,求出的长,即可求出的长.
21.【答案】解:过作于,交的延长线于,
则,
,
四边形是矩形,
,,
在中,,,
,,
,
在中,,,
,
,
答:木栈道的长度约为.
【解析】本题考查解直角三角形方向角问题,解题的关键是学会添加常用辅助线.构造直角三角形解决问题,属于中考常考题型.
过作于,交的延长线于,于是得到,推出四边形是矩形,得到,,解直角三角形即可得到结论.
22.【答案】解:如图,作,垂足为
,
;
在中,;
图又,
,
;
在和中,,
≌;
,
且,,
;
,
,
即到的距离是.
由知:≌,
,
作,垂足为.
,
,
,
即到地面的距离是.
【解析】本题主要考查了三角形全等的判定与性质的应用熟练掌握定理是解题的关键.
作,垂足为,利用三角形全等得到≌,根据三角形全等的性质得到,可以求出结果;
由知:≌,根据三角形全等的性质得到:, 作,垂足为,得到,可以求出结果.
23.【答案】解:过点作于点,
根据题意可得四边形是矩形,
,米,
在中,
,
,
,
在中,,
,
米.
答:观景台的高的值约为米.
【解析】本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
过点作于点,根据题意可得四边形是矩形,,,再根据锐角三角函数可得的长,进而可得的值.
24.【答案】解:过点作于过点作于.
矩形,,,.
,.
在中,.
,
点离地面的高度为.
【解析】作于,于,则四边形为矩形,得出,,求出,在中利用正弦可计算出,然后计算即可.
本题考查了解直角三角形的应用:先将实际问题抽象为数学问题,构造出直角三角形转化为解直角三角形问题,然后利用勾股定理和三角函数的定义进行计算.
25.【答案】解:作于点,于点,则.
梯形中,,
,
.
,
在直角中,,
则,则;
,
则建筑这个大坝共需土石料
答:建筑这个大坝共需土石料.
【解析】作于点,于点,在直角中,求得的长,即的长,在直角中即可求得的正切值,即可求解;
求得截面积,然后乘以即可求解.
本题考查了解直角三角形的应用,以及三角函数,解题的基本依据是转化为解直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
