3.2.2双曲线的简单几何性质(第三课时) 课件(共26张PPT)
文档属性
| 名称 | 3.2.2双曲线的简单几何性质(第三课时) 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 12:16:47 | ||
图片预览







文档简介
(共26张PPT)
3.2.2 双曲线的简单几何性质(第3课时)
微专题 直线与双曲线的位置关系
1.点与椭圆的位置关系
类比点与圆的位置关系的判定方法,尝试归纳点与椭圆位置关系的判定方法。
几何法:
d>r
d=r
d代数法
代数法
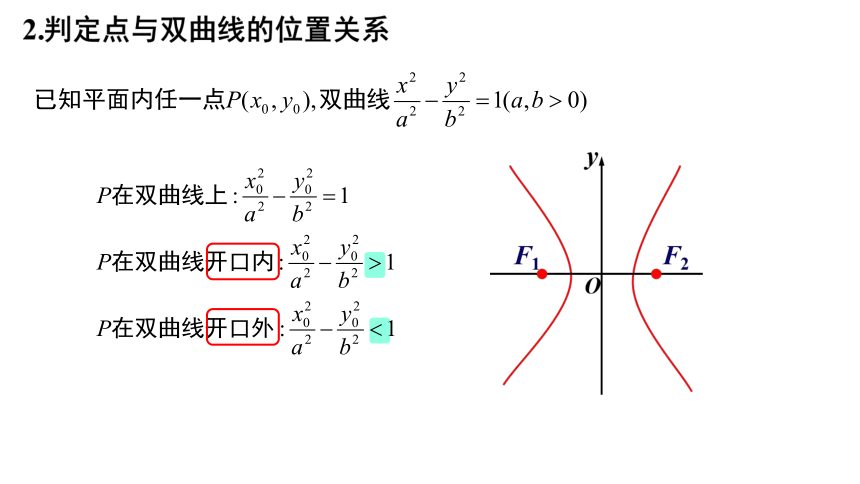
2.判定点与双曲线的位置关系
1.相离:
2.相切:
3.相交:
直线与椭圆组成的方程组无解
直线与椭圆组成的方程组只有一组解
直线与椭圆组成的方程组有两组解
当Δ>0时,方程有两解,直线与椭圆相交;
当Δ=0时,方程有一解,直线与椭圆相切;
当Δ<0时,方程无解 ,直线与椭圆相离.
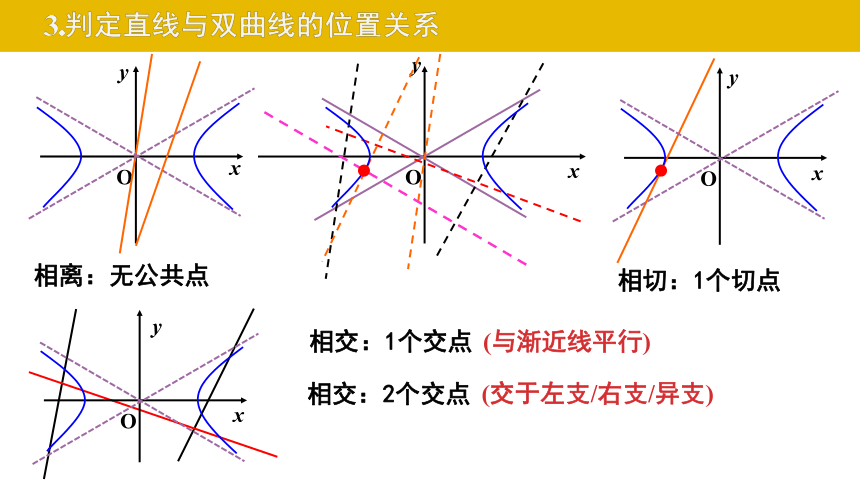
3.判定直线与双曲线的位置关系
y
O
相离:无公共点
相切:1个切点
相交:2个交点
x
(交于左支/右支/异支)
相交:1个交点
(与渐近线平行)
O
x
y
O
x
y
O
x
y
3.判定直线与双曲线的位置关系(代数法)
例1.已知直线 y=kx-1与双曲线x2-y2=4, 试讨论实数k的取值范围, 使直线与双曲线(1)无公共点; (2)有2个公共点; (3)只有1个公共点.
考虑二次项系数A是否为0
A=0时直线与渐近线平行
A≠0时才能考虑△
相切
相交于一点(平行于渐近线)
直线与双曲线的位置关系
位置关系及判定:
联立:
列式:
消元:
(b2-a2k2)x2-2a2kmx-a2(m2+b2)=0.
2
1
1
0
3.判定直线与双曲线的位置关系(代数法)
O
x
y
4.双曲线的弦长问题
解1:
例6
解2:
例6
变式
变式
4.双曲线的弦长问题
解1:
中点弦问题:
x
y
O
B
M
.
A
解2: (点差法)
x
y
O
B
M
.
A
中点弦问题:
解3:
x
y
O
B
M
.
A
中点弦问题:
x
y
O
A
M
.
B
4.双曲线的中点弦问题与点差法
[变式]已知双曲线3x2-y2=3,
证明:斜率为2的直线被双曲线所截得的弦的中点在一条直线上;
5.双曲线中的斜率乘积定值问题
焦点在x轴上:椭﹣双+
焦点在y轴上:颠倒a, b
巩固:双曲线中的斜率乘积定值问题
3.2.2 双曲线的简单几何性质(第3课时)
微专题 直线与双曲线的位置关系
1.点与椭圆的位置关系
类比点与圆的位置关系的判定方法,尝试归纳点与椭圆位置关系的判定方法。
几何法:
d>r
d=r
d
代数法
2.判定点与双曲线的位置关系
1.相离:
2.相切:
3.相交:
直线与椭圆组成的方程组无解
直线与椭圆组成的方程组只有一组解
直线与椭圆组成的方程组有两组解
当Δ>0时,方程有两解,直线与椭圆相交;
当Δ=0时,方程有一解,直线与椭圆相切;
当Δ<0时,方程无解 ,直线与椭圆相离.
3.判定直线与双曲线的位置关系
y
O
相离:无公共点
相切:1个切点
相交:2个交点
x
(交于左支/右支/异支)
相交:1个交点
(与渐近线平行)
O
x
y
O
x
y
O
x
y
3.判定直线与双曲线的位置关系(代数法)
例1.已知直线 y=kx-1与双曲线x2-y2=4, 试讨论实数k的取值范围, 使直线与双曲线(1)无公共点; (2)有2个公共点; (3)只有1个公共点.
考虑二次项系数A是否为0
A=0时直线与渐近线平行
A≠0时才能考虑△
相切
相交于一点(平行于渐近线)
直线与双曲线的位置关系
位置关系及判定:
联立:
列式:
消元:
(b2-a2k2)x2-2a2kmx-a2(m2+b2)=0.
2
1
1
0
3.判定直线与双曲线的位置关系(代数法)
O
x
y
4.双曲线的弦长问题
解1:
例6
解2:
例6
变式
变式
4.双曲线的弦长问题
解1:
中点弦问题:
x
y
O
B
M
.
A
解2: (点差法)
x
y
O
B
M
.
A
中点弦问题:
解3:
x
y
O
B
M
.
A
中点弦问题:
x
y
O
A
M
.
B
4.双曲线的中点弦问题与点差法
[变式]已知双曲线3x2-y2=3,
证明:斜率为2的直线被双曲线所截得的弦的中点在一条直线上;
5.双曲线中的斜率乘积定值问题
焦点在x轴上:椭﹣双+
焦点在y轴上:颠倒a, b
巩固:双曲线中的斜率乘积定值问题
