2023-2024学年苏科版数学九年级上册 期末综合试题训练(含答案)
文档属性
| 名称 | 2023-2024学年苏科版数学九年级上册 期末综合试题训练(含答案) | 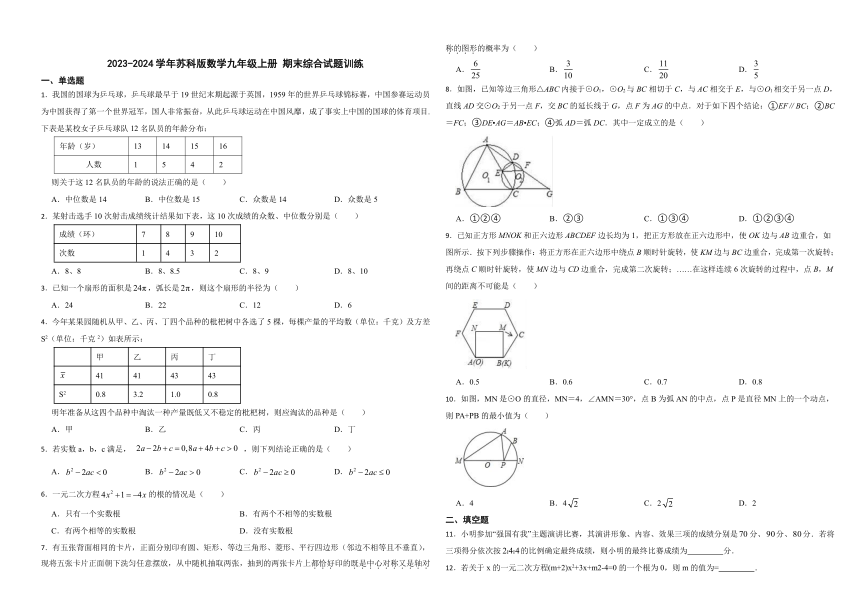 | |
| 格式 | docx | ||
| 文件大小 | 303.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 19:24:27 | ||
图片预览


文档简介
2023-2024学年苏科版数学九年级上册 期末综合试题训练
一、单选题
1.我国的国球为乒乓球,乒乓球最早于19世纪末期起源于英国,1959年的世界乒乓球锦标赛,中国参赛运动员为中国获得了第一个世界冠军,国人非常振奋,从此乒乓球运动在中国风靡,成了事实上中国的国球的体育项目.下表是某校女子乒乓球队12名队员的年龄分布:
年龄(岁) 13 14 15 16
人数 1 5 4 2
则关于这12名队员的年龄的说法正确的是( )
A.中位数是14 B.中位数是15 C.众数是14 D.众数是5
2.某射击选手10次射击成绩统计结果如下表,这10次成绩的众数、中位数分别是( )
成绩(环) 7 8 9 10
次数 1 4 3 2
A.8、8 B.8、8.5 C.8、9 D.8、10
3.已知一个扇形的面积是,弧长是,则这个扇形的半径为( )
A.24 B.22 C.12 D.6
4.今年某果园随机从甲、乙、丙、丁四个品种的枇杷树中各选了5棵,每棵产量的平均数(单位:千克)及方差S2(单位:千克2)如表所示:
甲 乙 丙 丁
41 41 43 43
S2 0.8 3.2 1.0 0.8
明年准备从这四个品种中淘汰一种产量既低又不稳定的枇杷树,则应淘汰的品种是( )
A.甲 B.乙 C.丙 D.丁
5.若实数a,b,c满足, ,则下列结论正确的是( )
A. B. C. D.
6.一元二次方程的根的情况是( )
A.只有一个实数根 B.有两个不相等的实数根
C.有两个相等的实数根 D.没有实数根
7.有五张背面相同的卡片,正面分别印有圆、矩形、等边三角形、菱形、平行四边形(邻边不相等且不垂直),现将五张卡片正面朝下洗匀任意摆放,从中随机抽取两张,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为( )
A. B. C. D.
8.如图,已知等边三角形△ABC内接于⊙O1,⊙O2与BC相切于C,与AC相交于E,与⊙O1相交于另一点D,直线AD交⊙O2于另一点F,交BC的延长线于G,点F为AG的中点.对于如下四个结论:①EF∥BC;②BC=FC;③DE AG=AB EC;④弧AD=弧DC.其中一定成立的是( )
A.①②④ B.②③ C.①③④ D.①②③④
9.已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B,M间的距离不可能是( )
A.0.5 B.0.6 C.0.7 D.0.8
10.如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
A.4 B.4 C.2 D.2
二、填空题
11.小明参加“强国有我”主题演讲比赛,其演讲形象、内容、效果三项的成绩分别是分、分、分.若将三项得分依次按的比例确定最终成绩,则小明的最终比赛成绩为 分.
12.若关于x的一元二次方程(m+2)x2+3x+m2-4=0的一个根为0,则m的值为= .
13.如图,有A、B、C三类长方形(或正方形)卡片(a>b),其中甲同学持有A、B类卡片各一张,乙同学持有B、C类卡片各一张,丙同学持有A、C类卡片各一张,现随机选取两位同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是 .
14.体育中考前夕,某校将九年级部分男生分成五组,进行了跳绳模拟测试,经统计,这五个小组平均每分钟跳绳次数如下:180,190,x,176,180.若该组数据的众数与平均数相等,那么这组数据的中位数是 .
15.已知关于x的一元二次方程x2+ax+nb=0(1≤n≤3,n为整数),其中a是从2、4、6三个数中任取的一个数,b是从1、3、5三个数中任取的一个数,定义“方程有实数根”为事件An(n=1,2,3),当An的概率最小时,n的所有可能值为 .
16.若关于的方程有三个解,则实数的值是 .
三、计算题
17.解方程: .
18.解方程
(1)
(2)
四、解答题
19.如图,阴影部分是一广告标志,已知两圆弧所在圆的半径分别是20cm,10cm,∠AOB=120°,则这个广告标志的周长是多少?
20.某小区为促进生活垃圾的分类处理,将生活垃圾分为a(厨余)、b(可回收)、c(其他)三类,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱分别记为A、B、C.粗心的小亮将分类好的两袋垃圾(可回收、其他)随机投入到三种垃圾箱的其中两种内,请用画树状图或列表格的方法,求小亮投放正确的概率.
21.如图,在 中, 为 的直径, ,点 为 上任意一点(不与 、 重合).
求证: .
22.学校广播站要招收一名播音员,考查形象、知识面、普通话三个项目,按形象占10%,知识面占40%,普通话占50%,计算加权平均数,作为最后评定的总成绩,若总成绩超过85分,则可进入候选名单.已知张强的形象、知识面、普通话三项的成绩依次为90分、80分、90分,计算并说明张强能否进入候选名单?
23.k取什么值时,关于x的方程 有两个相等的实数根?求出这时方程的根.
24. 如图,一农户原来种植的花生,每公顷产量为,出油率为即每花生可加工出花生油现在种植新品种花生后,每公顷收获的花生可加工出花生油,已知花生出油率的增长率是产量增长率的,求新品种花生产量的增长率.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】82
12.【答案】2
13.【答案】
14.【答案】180
15.【答案】2或3
16.【答案】9
17.【答案】 a=3,b=-2,c=-2,
b2-4ac=(-2)2-4×3×(-2)=28>0,
∴x= = ,
, .
18.【答案】(1)解:,
即(x-1)2=0,
∴x1=x2=1
(2)解:,
因式分解得:(2x-1)(x-3)=0,
∴2x-1=0或x-3=0,
∴x1=,x2=3
19.【答案】解: ,AC=BD=20-10=10cm,
∴周长=( )cm
20.【答案】解:树状图如下:
总共有6种可能情况,投放正确只有一种;
∴小亮投放正确的概率为: .
21.【答案】证明: ,
,
,
、 是 的半径,
,
在 和 中,
,
.
22.【答案】解: (分),
即张强的总成绩为86分.
∵86>85,
∴张强能进入候选名单.
23.【答案】解:∵关于x的方程4x2-(k+2)x+k-1=0有两个相等的实数根,
∴△=[-(k+2)]2-4×4×(k-1)=k2-12k+20=0,
解得:k1=2, k2=10
∴k=2或10时,关于x的方程4x2-(k+2)x+k-1=0有两个相等的实数根.
当k=2时,原方程为:4x2-4x+1=0,即(2x-1)2=0,解得:x1=x2= ;
当k=10时,原方程为:4x2-12x+9=0,即(2x-3)2=0,解得:x1=x2= ;
24.【答案】解:设新品种花生产量的增长率为,则新品种花生出油率的增长率为,
根据题意得:,
整理得:,
解得:,不符合题意,舍去.
答:新品种花生产量的增长率为.
一、单选题
1.我国的国球为乒乓球,乒乓球最早于19世纪末期起源于英国,1959年的世界乒乓球锦标赛,中国参赛运动员为中国获得了第一个世界冠军,国人非常振奋,从此乒乓球运动在中国风靡,成了事实上中国的国球的体育项目.下表是某校女子乒乓球队12名队员的年龄分布:
年龄(岁) 13 14 15 16
人数 1 5 4 2
则关于这12名队员的年龄的说法正确的是( )
A.中位数是14 B.中位数是15 C.众数是14 D.众数是5
2.某射击选手10次射击成绩统计结果如下表,这10次成绩的众数、中位数分别是( )
成绩(环) 7 8 9 10
次数 1 4 3 2
A.8、8 B.8、8.5 C.8、9 D.8、10
3.已知一个扇形的面积是,弧长是,则这个扇形的半径为( )
A.24 B.22 C.12 D.6
4.今年某果园随机从甲、乙、丙、丁四个品种的枇杷树中各选了5棵,每棵产量的平均数(单位:千克)及方差S2(单位:千克2)如表所示:
甲 乙 丙 丁
41 41 43 43
S2 0.8 3.2 1.0 0.8
明年准备从这四个品种中淘汰一种产量既低又不稳定的枇杷树,则应淘汰的品种是( )
A.甲 B.乙 C.丙 D.丁
5.若实数a,b,c满足, ,则下列结论正确的是( )
A. B. C. D.
6.一元二次方程的根的情况是( )
A.只有一个实数根 B.有两个不相等的实数根
C.有两个相等的实数根 D.没有实数根
7.有五张背面相同的卡片,正面分别印有圆、矩形、等边三角形、菱形、平行四边形(邻边不相等且不垂直),现将五张卡片正面朝下洗匀任意摆放,从中随机抽取两张,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为( )
A. B. C. D.
8.如图,已知等边三角形△ABC内接于⊙O1,⊙O2与BC相切于C,与AC相交于E,与⊙O1相交于另一点D,直线AD交⊙O2于另一点F,交BC的延长线于G,点F为AG的中点.对于如下四个结论:①EF∥BC;②BC=FC;③DE AG=AB EC;④弧AD=弧DC.其中一定成立的是( )
A.①②④ B.②③ C.①③④ D.①②③④
9.已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B,M间的距离不可能是( )
A.0.5 B.0.6 C.0.7 D.0.8
10.如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
A.4 B.4 C.2 D.2
二、填空题
11.小明参加“强国有我”主题演讲比赛,其演讲形象、内容、效果三项的成绩分别是分、分、分.若将三项得分依次按的比例确定最终成绩,则小明的最终比赛成绩为 分.
12.若关于x的一元二次方程(m+2)x2+3x+m2-4=0的一个根为0,则m的值为= .
13.如图,有A、B、C三类长方形(或正方形)卡片(a>b),其中甲同学持有A、B类卡片各一张,乙同学持有B、C类卡片各一张,丙同学持有A、C类卡片各一张,现随机选取两位同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是 .
14.体育中考前夕,某校将九年级部分男生分成五组,进行了跳绳模拟测试,经统计,这五个小组平均每分钟跳绳次数如下:180,190,x,176,180.若该组数据的众数与平均数相等,那么这组数据的中位数是 .
15.已知关于x的一元二次方程x2+ax+nb=0(1≤n≤3,n为整数),其中a是从2、4、6三个数中任取的一个数,b是从1、3、5三个数中任取的一个数,定义“方程有实数根”为事件An(n=1,2,3),当An的概率最小时,n的所有可能值为 .
16.若关于的方程有三个解,则实数的值是 .
三、计算题
17.解方程: .
18.解方程
(1)
(2)
四、解答题
19.如图,阴影部分是一广告标志,已知两圆弧所在圆的半径分别是20cm,10cm,∠AOB=120°,则这个广告标志的周长是多少?
20.某小区为促进生活垃圾的分类处理,将生活垃圾分为a(厨余)、b(可回收)、c(其他)三类,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱分别记为A、B、C.粗心的小亮将分类好的两袋垃圾(可回收、其他)随机投入到三种垃圾箱的其中两种内,请用画树状图或列表格的方法,求小亮投放正确的概率.
21.如图,在 中, 为 的直径, ,点 为 上任意一点(不与 、 重合).
求证: .
22.学校广播站要招收一名播音员,考查形象、知识面、普通话三个项目,按形象占10%,知识面占40%,普通话占50%,计算加权平均数,作为最后评定的总成绩,若总成绩超过85分,则可进入候选名单.已知张强的形象、知识面、普通话三项的成绩依次为90分、80分、90分,计算并说明张强能否进入候选名单?
23.k取什么值时,关于x的方程 有两个相等的实数根?求出这时方程的根.
24. 如图,一农户原来种植的花生,每公顷产量为,出油率为即每花生可加工出花生油现在种植新品种花生后,每公顷收获的花生可加工出花生油,已知花生出油率的增长率是产量增长率的,求新品种花生产量的增长率.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】82
12.【答案】2
13.【答案】
14.【答案】180
15.【答案】2或3
16.【答案】9
17.【答案】 a=3,b=-2,c=-2,
b2-4ac=(-2)2-4×3×(-2)=28>0,
∴x= = ,
, .
18.【答案】(1)解:,
即(x-1)2=0,
∴x1=x2=1
(2)解:,
因式分解得:(2x-1)(x-3)=0,
∴2x-1=0或x-3=0,
∴x1=,x2=3
19.【答案】解: ,AC=BD=20-10=10cm,
∴周长=( )cm
20.【答案】解:树状图如下:
总共有6种可能情况,投放正确只有一种;
∴小亮投放正确的概率为: .
21.【答案】证明: ,
,
,
、 是 的半径,
,
在 和 中,
,
.
22.【答案】解: (分),
即张强的总成绩为86分.
∵86>85,
∴张强能进入候选名单.
23.【答案】解:∵关于x的方程4x2-(k+2)x+k-1=0有两个相等的实数根,
∴△=[-(k+2)]2-4×4×(k-1)=k2-12k+20=0,
解得:k1=2, k2=10
∴k=2或10时,关于x的方程4x2-(k+2)x+k-1=0有两个相等的实数根.
当k=2时,原方程为:4x2-4x+1=0,即(2x-1)2=0,解得:x1=x2= ;
当k=10时,原方程为:4x2-12x+9=0,即(2x-3)2=0,解得:x1=x2= ;
24.【答案】解:设新品种花生产量的增长率为,则新品种花生出油率的增长率为,
根据题意得:,
整理得:,
解得:,不符合题意,舍去.
答:新品种花生产量的增长率为.
同课章节目录
