绝对值相关复习
图片预览








文档简介
课件36张PPT。绝对值相关复习
谁能逃离危险60公里/小时110公里/小时80公里/小时30公里/小时40公里/小时炸弹30秒钟后爆炸,500米以外是安全地带. 爆炸时, 小狗距爆炸地点140米,小狗的奔跑速度是多少公里/小时?
当我们研究怎样能逃离危险地带时,主要考虑的是什么问题? 想一想讨论什么叫一个数的绝对值?oxba讨论1.绝对值的几何意义(结合数轴说明);
2.用文字语言和符号语言分别叙述绝对值的代数意义.
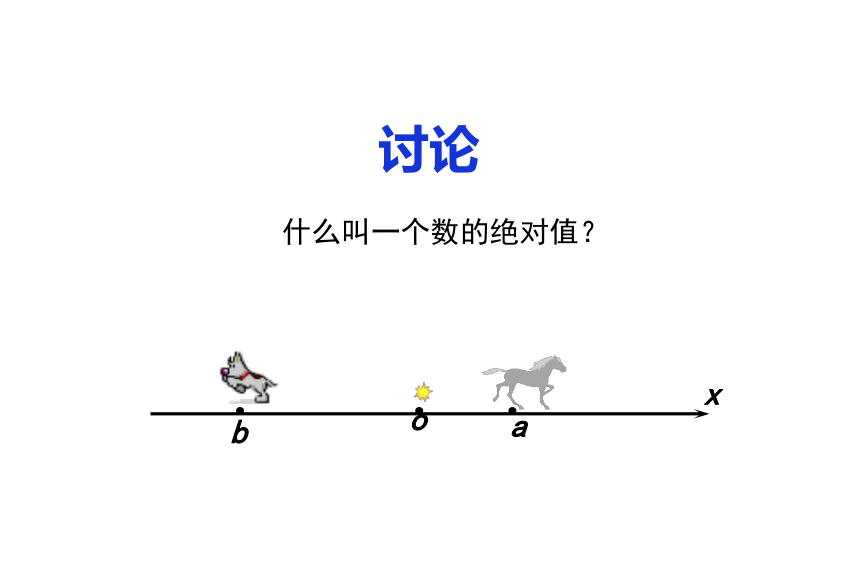
一个数a的绝对值就是数轴上表示数a的点与原点的距离.
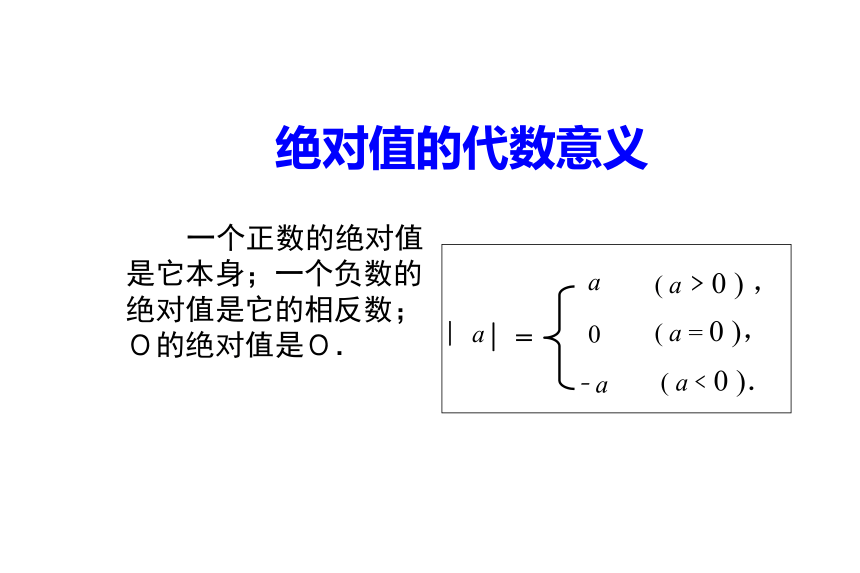
注意:距离不会出现负数,因而绝对值最小值是0. 绝对值的几何意义 一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.绝对值的代数意义例1 如果|x|=8,求x.
解:∵|+8|=8,|-8|=8,
∴ x=+8,或x=-8.例2 写出绝对值小于3.9的整数.
解:绝对值小于3.9的整数有:
-3,-2,-1,0,1,2,3. 例3 若|m|=-m,则 m是怎样的数?
解:∵当m<0时 |m|=-m,
又∵ 0的相反数是0,
∴ m可以是一切负数或零. 小结1.a的绝对值永远是非负数,即|a|≥0;
2.一对相反数的绝对值为同一个数;
3.绝对值相等的两数相等或者互为相反数;
4.为化简|a|(去掉绝对值符号),需要先
明确a的,然后再根据绝对值的代数
意义化简.解有关绝对值问题的关键 根据题中已知或隐含条件去掉绝值符号,或者对绝对值号内的数(或代数式)的符号进行讨论,去掉绝值符号. 例4 已知:|x-2|+x-2=0,
求:(1)x+2的最大值;(2)6-x的最小值.
解:∵|x-2|+x-2=0,
∴|x-2|=-(x-2).
∴x-2≤0,即x≤2,x的最大值为2.
(1)当x=2时,x+2取得最大值2+2=4;
(2)当x=2时,6-x取得最小值6-2=4.例5 化简:|1-3x|+|1+2x|.
解:1
21
3(1)当x<- —时,1-3x>0,1+2x<0,∴原式=(1-3x)+[-(1+2x)]=-5x;∴原式=(1-3x)+(1+2x)=2-x.(3)当x≥—时,1-3x≤0,1+2x>0,∴原式=-(1-3x)+(1+2x)=5x. 想一想化简:|3x-1|+|2x+1|. 例5 有理数a、b、c在数轴上的位置如图所示,则式子|a|+|b|+|a+b|+|b-c|化简结果为 [ ].
A.2a+3b-c B.3b-c.
C.b+c D.c-b.解:由图形可知a<0,c>b>0,
且|c|>|b|>|a|,
则a+b>0,b-c<0.
所以原式=-a+b+a+b-b+c=b+c,
故应选(C).分析智力竞赛必答题1、下列说法正确的是( ).
A.绝对值等于它本身的数只有0;
B.绝对值等于它本身的数是正数;
C.绝对值等于它本身的数有0和正数;
D.绝对值等于它本身的数的相反数是负数. CA 2.如果 ,则( ).
A. a>0 ; B. a<0;
C. a≥0 ; D. a≤0.D
3.若x为任意有理数,则-|-x|一定是( ).
A.正数; B.负数;
C.正数或零; D.负数或零.
4.求绝对值不大于2的整数.
-2, -1, 0, 1, 2.
5.下列各式错误的是( )
A. -5.33>-5— B.-4<-3<-2;
C. |-0.125|< — ; D.-(+2)<|-3|.1
3;1
8C 6.下列说法正确的是( )。
A.0是绝对值最小的数;
B.绝对值较大的数较大;
C.如果两个数的绝对值相等,则
这两个数一定相等;
D.一个数的倒数乘它本身的积是1.A 7.如果|x|=-x ,那么x的值是( )。
A.正数; B.负数;
C.非负数; D.非正数.D8.设x<-1,化简 2-|2-|x-2||的结果是( ).
A. x ; B.2+x;
C.-2+x; D.-2-x.B 9.若两个数的和是正数,则这两个数( ).
A.都是正数 ;
B.只有一个是正数;
C.有一个必为0;
D.一定至少有一个是正数.D 10.数轴上表示+7的点是A,表示-4的点是
B,则A、B两点间的距离是( ).
A. 3; B. -3;
C. 11; D.-11.C 11.一个数的倒数等于它本身的数一共有( ).
A.1个; B.2个;
C.3个; D.4个. B 12.如果一个数的相反数是非正数,则
这个数一定是( )
A.正数 ; B.负数;
C.非负数 ; D.非正数. C抢答题 1.已知:|a|=3,|b|=2.
求:a+b的值. 5,1,-1,-5 2.|x-3|+|y-2|=0 成立的条件是( ).
A. x=3 ; B. y=2;
C. x=3且y=2; D. x、y为任意数.C3.已知:x<0,y>0,且|x|<|y|,则( ).
A. -y<-x<x<y ;
B. -x<x<-y<y ;
C. -y<x<-x<y ;
D. -y<y<-x<x.C 4.|x-2|+|x-1|+|x-3|的最小值是 ( ).
A.1; B.2 ;
C.3; D.4.B5. 若|x-5|+|y+2|=0,则x-y=______. 7 在学习绝对值的过程中,我们利用了数轴,这体现了数形结合的思想.
我们把有理数分为正数、负数或者零去加以研究和讨论,这应用了分类讨论的思想方法. 小结
谁能逃离危险60公里/小时110公里/小时80公里/小时30公里/小时40公里/小时炸弹30秒钟后爆炸,500米以外是安全地带. 爆炸时, 小狗距爆炸地点140米,小狗的奔跑速度是多少公里/小时?
当我们研究怎样能逃离危险地带时,主要考虑的是什么问题? 想一想讨论什么叫一个数的绝对值?oxba讨论1.绝对值的几何意义(结合数轴说明);
2.用文字语言和符号语言分别叙述绝对值的代数意义.
一个数a的绝对值就是数轴上表示数a的点与原点的距离.
注意:距离不会出现负数,因而绝对值最小值是0. 绝对值的几何意义 一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.绝对值的代数意义例1 如果|x|=8,求x.
解:∵|+8|=8,|-8|=8,
∴ x=+8,或x=-8.例2 写出绝对值小于3.9的整数.
解:绝对值小于3.9的整数有:
-3,-2,-1,0,1,2,3. 例3 若|m|=-m,则 m是怎样的数?
解:∵当m<0时 |m|=-m,
又∵ 0的相反数是0,
∴ m可以是一切负数或零. 小结1.a的绝对值永远是非负数,即|a|≥0;
2.一对相反数的绝对值为同一个数;
3.绝对值相等的两数相等或者互为相反数;
4.为化简|a|(去掉绝对值符号),需要先
明确a的,然后再根据绝对值的代数
意义化简.解有关绝对值问题的关键 根据题中已知或隐含条件去掉绝值符号,或者对绝对值号内的数(或代数式)的符号进行讨论,去掉绝值符号. 例4 已知:|x-2|+x-2=0,
求:(1)x+2的最大值;(2)6-x的最小值.
解:∵|x-2|+x-2=0,
∴|x-2|=-(x-2).
∴x-2≤0,即x≤2,x的最大值为2.
(1)当x=2时,x+2取得最大值2+2=4;
(2)当x=2时,6-x取得最小值6-2=4.例5 化简:|1-3x|+|1+2x|.
解:1
21
3(1)当x<- —时,1-3x>0,1+2x<0,∴原式=(1-3x)+[-(1+2x)]=-5x;∴原式=(1-3x)+(1+2x)=2-x.(3)当x≥—时,1-3x≤0,1+2x>0,∴原式=-(1-3x)+(1+2x)=5x. 想一想化简:|3x-1|+|2x+1|. 例5 有理数a、b、c在数轴上的位置如图所示,则式子|a|+|b|+|a+b|+|b-c|化简结果为 [ ].
A.2a+3b-c B.3b-c.
C.b+c D.c-b.解:由图形可知a<0,c>b>0,
且|c|>|b|>|a|,
则a+b>0,b-c<0.
所以原式=-a+b+a+b-b+c=b+c,
故应选(C).分析智力竞赛必答题1、下列说法正确的是( ).
A.绝对值等于它本身的数只有0;
B.绝对值等于它本身的数是正数;
C.绝对值等于它本身的数有0和正数;
D.绝对值等于它本身的数的相反数是负数. CA 2.如果 ,则( ).
A. a>0 ; B. a<0;
C. a≥0 ; D. a≤0.D
3.若x为任意有理数,则-|-x|一定是( ).
A.正数; B.负数;
C.正数或零; D.负数或零.
4.求绝对值不大于2的整数.
-2, -1, 0, 1, 2.
5.下列各式错误的是( )
A. -5.33>-5— B.-4<-3<-2;
C. |-0.125|< — ; D.-(+2)<|-3|.1
3;1
8C 6.下列说法正确的是( )。
A.0是绝对值最小的数;
B.绝对值较大的数较大;
C.如果两个数的绝对值相等,则
这两个数一定相等;
D.一个数的倒数乘它本身的积是1.A 7.如果|x|=-x ,那么x的值是( )。
A.正数; B.负数;
C.非负数; D.非正数.D8.设x<-1,化简 2-|2-|x-2||的结果是( ).
A. x ; B.2+x;
C.-2+x; D.-2-x.B 9.若两个数的和是正数,则这两个数( ).
A.都是正数 ;
B.只有一个是正数;
C.有一个必为0;
D.一定至少有一个是正数.D 10.数轴上表示+7的点是A,表示-4的点是
B,则A、B两点间的距离是( ).
A. 3; B. -3;
C. 11; D.-11.C 11.一个数的倒数等于它本身的数一共有( ).
A.1个; B.2个;
C.3个; D.4个. B 12.如果一个数的相反数是非正数,则
这个数一定是( )
A.正数 ; B.负数;
C.非负数 ; D.非正数. C抢答题 1.已知:|a|=3,|b|=2.
求:a+b的值. 5,1,-1,-5 2.|x-3|+|y-2|=0 成立的条件是( ).
A. x=3 ; B. y=2;
C. x=3且y=2; D. x、y为任意数.C3.已知:x<0,y>0,且|x|<|y|,则( ).
A. -y<-x<x<y ;
B. -x<x<-y<y ;
C. -y<x<-x<y ;
D. -y<y<-x<x.C 4.|x-2|+|x-1|+|x-3|的最小值是 ( ).
A.1; B.2 ;
C.3; D.4.B5. 若|x-5|+|y+2|=0,则x-y=______. 7 在学习绝对值的过程中,我们利用了数轴,这体现了数形结合的思想.
我们把有理数分为正数、负数或者零去加以研究和讨论,这应用了分类讨论的思想方法. 小结
