第六章 数据的分析教案
图片预览




文档简介
第六章 数据的分析
6.1 平均数、中位数、众数
6.1.1 平均数(1)
教学目标
使学生掌握平均数的计算方法;
通过本节课的学习,还应使学生理解平均数在 ( http: / / www.21cnjy.com )数据统计中的意义和作用:描述一组数据集中趋势的特征数字,是反映一组数据平均水平的特征数,并认识平均数的优、缺点.
教学重点、难点
1.重点:理解平均数的意义.
2.难点:认识平均数的优、缺点.
教学过程
一、自主学习
通过预习教材P137~P139的内容,完成下面各题.
1.要比较三种棉花哪个品种更好,应比较这三种棉花的___平均结桃数_______.
2.平均数是一组数据的数值的代表值,它刻画了这组数据 整体 平均状态,对于这组数据的 个体性质 不能作什么结论.
3.平均数的缺点是:___容易受个别特殊值的影响_______.
二、尝试应用
1.填空:783,769,774,779,765的平均数是 .
2.填空:在由某电视台举办的唱歌比赛中,由 ( http: / / www.21cnjy.com )10位评委现场给每位歌手打分,然后去掉其中的一个最高分和一个最低分,其余分数的平均数作为该歌手的成绩.已知10位评委给歌手潘多打分是9.5,9.5,9.3,9.8,,9.4,9.1,9.6,9.5,9.2,9.6,则潘多的得分是 (结果保留到小数点后第2位).
3.某班进行了一次数学测验,
第一组的成绩是:56,32,63,74,85,22,44,78,91,65;
第二组的成绩是:46,39,75,83,16,94,66,60,57,72.
请问:哪个组的成绩好?
(答案:因为,第一组平均成绩为==61
第二组平均成绩为==60.8
所以,第一组成绩好些.)
4.若不选择教材中的引入问题,也可以替换成更贴近学生学习生活中的实例,下举一例可供借鉴参考。
某校初二年级共有4个班,在一次数学考试中参考人数和成绩如下:
班级 1班 2班 3班 4班
参考人数 40 42 45 32
平均成绩 80 81 82 79
求该校初二年级在这次数学考试中的平均成绩?下述计算方法是否合理?为什么?
=(79+80+81+82)=80.5
.
三、当堂检测
1.填空:43,50,71,64的平均数是 .
2.填空:一个中学足球队的20名队员的身高如下(单位:厘米):
170,167,171,168,160,1 ( http: / / www.21cnjy.com )72,168,162,172,169,164,174,169,165,175,170,165,167,170,172,则这些队员的平均身高为 厘米.
3.填空:拉萨今年1月上旬各天的最低气温依次是(单位:℃):
-6,-5,-7,-7,-6,-4,-5,-7,-8,-7,则它们的平均气温为 ℃.
4.在“创优”活动中,我市 ( http: / / www.21cnjy.com )某校开展收集废旧电池的活动,该校8年级(1)班为估计4月份收集电池的个数,随机抽取了该月7天收集废旧电池的个数,数据如下:
48,51,53,47,49,50,52.
求这7天该班收集废旧电池的总个数,并估计4月份该班收集废旧电池的个数.
5.个体户张某经营一家餐馆,下面是该餐馆所有工作人员2001年10月份的工资.
张某:4000元;会计:700元;厨师 ( http: / / www.21cnjy.com )甲:1000元;厨师乙:900元;杂工甲:580元;杂工乙:560元;服务员甲:620元;服务员乙:600元;服务员丙:580.
(1)计算他们的平均工资;
(2)不计张某的工资,再求餐馆员工月平均工资.
四、本节小结
平均数计算要用到所有的数据,它能够充分利用所有的数据信息,但它受极端值的影响较大.
五、课后作业
(1)课本第139页练习题
(2)课本第147页习题第1、2题;
6.1.2 平均数(2)
教学目标
1.使学生理解数据的权和加权平均数的概念
2.使学生掌握加权平均数的计算方法
3.会根据加权平均数解决一些实际问题
教学重点、难点
1.重点:会计算加权平均数.
2.难点:对数据权概念的理解.
教学过程
一、自主学习
通过预习教材P139~P141的内容,完成下面各题.
1.填一填:在计算加权平均数时,权 ( http: / / www.21cnjy.com )数可以表示____________________________________:权数之和为_____,权数越大的数据在总体中所占的____________,它对加权平均数的______________.
2.求21、32、43、54分别以0.1、0.2、0.3、0.4为权的加权平均数.
3.在计算加权平均数时,常用________来反映对应的数据的________程度:权数________的数据___________.
二、尝试应用
1.在一次英语口试中,已知50分1 ( http: / / www.21cnjy.com )人、60分2人、70分5人、90分5人、100分1人,其余为84分。已知该班平均成绩为80分,问该班有多少人?
2.一家公司打算招聘一名部门经理,现对甲、乙 ( http: / / www.21cnjy.com )两名应聘者从笔试、面试、实习成绩三个方面表现进行评分,笔试占总成绩20%、面试占30%、实习成绩占50%,各项成绩如表所示:
应聘者 笔试 面试 实习
甲 85 83 90
乙 80 85 92
试判断谁会被公司录取,为什么?
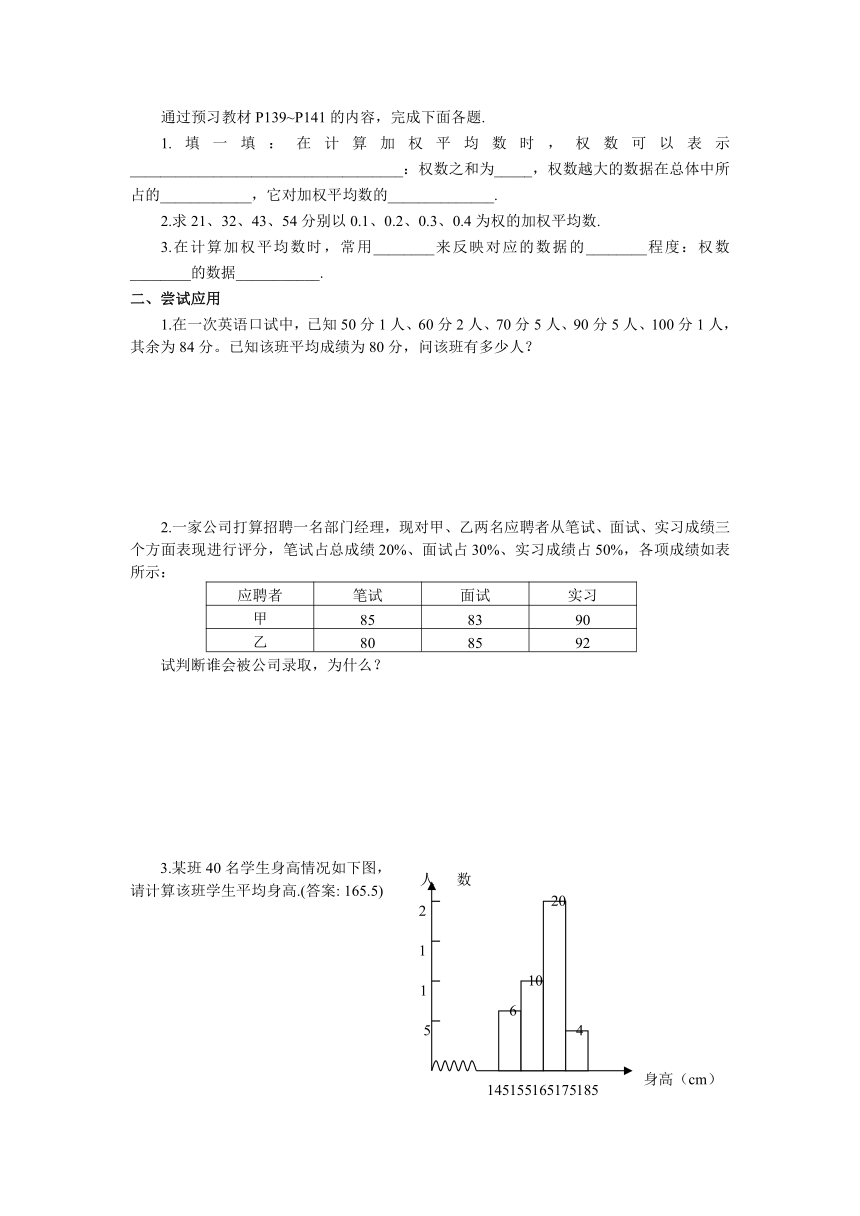
3.某班40名学生身高情况如下图,
请计算该班学生平均身高.(答案: 165.5)
三、当堂检测
1.某人打靶有a次打中环,b次打中环,则此人平均每次中靶 环.
2.老师在计算学期总平均分的时候按如下标准:作业占100%、测验占30%、期中占35%、期末考试占35%,小关和小兵的成绩如下表:
学生 作业 测验 期中考试 期末考试
小关 80 75 71 88
小兵 76 80 68 90
试比较两人谁的成绩好?
四、本节小结
1.这节课我们学到了什么知识?
2.我们感受到了什么
3.还存在什么疑惑?
五、课后作业
(1)课本第142页练习题;
(2)课本第147-148页习题第3、5题.
6.1.2 中位数
教学目标
1.认识中位数,并会求出一组数据中的中位数.
2.理解中位数的意义和作用。它也是数据代表,可以反映一定的数据信息,帮助人们在实际问题中分析并做出决策.
3.会利用中位数分析数据信息做出决策.
教学重点、难点
1.重点:认识中位数这种数据代表.
2.难点:利用中位数分析数据信息做出决策.
教学过程
一、自主学习
通过预习教材P142~P143的内容,完成下面各题.
1.把一组数据___________的顺序排列,如果数据的个数是_____数,那么位于_______的数称为这组数据的中位数.如果数据的个数是_____数,那么位于中间的____个数的平均数称为这组数据的中位数.
2.优点:中位数把一组数 ( http: / / www.21cnjy.com )据分成数目________的两部分,其中一部分_______或_______中位数,而另一部分_______或_______中位数,因此,中位数常用来描述__________________.
3.缺点:它没有利用数据中_________信息,因此,有时它可能不是____________.
二、尝试应用
数据8、9、9、8、10、8、9、8、10、7、9、9、8的中位数是 .
一组数据23、27、20、18、X、12,它的中位数是21,则X的值是 .
3.某公司销售部有营销人员15人,销售部为了制定某种商品的销售金额,统计了这15个人的销售量如下(单位:件)
1800、510、250、250、210、250、210、210、150、210、150、120、120、210、150
求这15个销售员该月销量的中位数.
假设销售部负责人把每位营销员的月销售定额定为320件,你认为合理吗?如果不合理,请你制定一个合理的销售定额并说明理由.
4.随机抽取我市一年(按365天计)中的30天平均气温状况如下表:
温度(℃) -8 -1 7 15 21 24 30
天数 3 5 5 7 6 2 2
请你根据上述数据回答问题:
(1).该组数据的中位数是什么?
(2).若当气温在18℃~25℃为市民“满意温度”,则我市一年中达到市民“满意温度”的大约有多少天?
答案:1. 9; 2. 22; ( http: / / www.21cnjy.com ) 3. (1)210件 (2)不合理。因为15人中有13人的销售额达不到320件(320虽是原始数据的平均数,却不能反映营销人员的一般水平),销售额定为210件合适,因为它既是中位数,是大部分人能达到的额定. 4.(1)15. (2)约97天
三、当堂检测
1.公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄如下:(单位:岁)
甲群:13、13、14、15、15、15、16、17、17.
乙群:3、4、4、5、5、6、6、6、54、57.
(1)、甲群游客的平均年龄是 岁,中位数是 岁,其中能较好反映甲群游客年龄特征的是 。
(2)、乙群游客的平均年龄是 岁,中位数是 岁,其中能较好反映乙群游客年龄特征的是 。
2.某公司有15名员工,它们所在的部门及相应每人所创的年利润如下表示:
部门 A B C D E F G
人数 1 1 2 4 2 2 3
每人所创的年利润 20 5 2.5 2.1 1.5 1.5 1.2
根据表中的信息填空:
该公司每人所创年利润的平均数是 万元。
该公司每人所创年利润的中位数是 万元。
你认为应该使用平均数和中位数中哪一个来描述该公司每人所创年利润的一般水平?答
答案:1.(1)15、15、中位数; (2)15、5.5、中位数.
2.(1)3.2万元 (2)2.1万元 (3)中位数
四、本节小结
中位数仅与数据的排列位置有关,某些数据 ( http: / / www.21cnjy.com )的移动对中位数没有影响,中位数可能出现在所给数据中也可能不在所给的数据中,当一组数据中的个别数据变动较大时,可用中位数描述其趋势.
五、课后作业
(1)课本第144页练习题
(2)课本第148页习题第6题;
6.1.3 众数
教学目标
1.认识众数,并会求出一组数据中的众数.
2.理解众数的意义和作用。它也是数据代表,可以反映一定的数据信息,帮助人们在实际问题中分析并做出决策.
3.会利用众数分析数据信息做出决策.
教学重点、难点
1.重点:认识中位数、众数这两种数据代表.
2.难点:利用中位数、众数分析数据信息做出决策.
教学过程
一、自主学习
通过预习教材P144~P146的内容,完成下面各题.
1.什么是众数?____________________________________________________.
2.自学完例4后,你认为该公司总经理、普通职工以及应聘者将分别关注职工月工资数据的平均数、中位数和众数中的哪一个?为什么
3.思考:众数有什么特点,它的优点 ( http: / / www.21cnjy.com )是什么?缺点是什么?众数是一组数据中的出现次数___________的数,众数可以不止____________.
优点:容易_________,当一组数据中某数多次出现时,可以用众数作为这组数据的数值的_______________.
缺点:众数不能充分利用数据中______________,因此众数不能经常使用.
尝试应用
1.如果在一组数据中,23、25、28、 ( http: / / www.21cnjy.com )22出现的次数依次为2、5、3、4次,并且没有其他的数据,则这组数据的众数和中位数分别是( )
A.24、25 B.23、24 C.25、25 D.23、25
2.数据92、96、98、100、X的众数是96,则其中位数和平均数分别是( )
A.97、96 B.96、96.4 C.96、97 D.98、97
3.某商店3、4月份出售某一品牌各种规格的空调,销售台数如表所示:
1匹 1.2匹 1.5匹 2匹
3月 12台 20台 8台 4台
4月 16台 30台 14台 8台
根据表格回答问题:
商店出售的各种规格空调中,众数是多少?
假如你是经理,现要进货,6月份在有限的资金下进货单位将如何决定?
答案:1.C; 2.B; 3 ( http: / / www.21cnjy.com ).(1)1.2匹 (2)通过观察可知1.2匹的销售最大,所以要多进1.2匹,由于资金有限就要少进2匹空调.
三、当堂检测
1.某公司的33名职工的月工资(以元为单位)如下:
职员 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5000 3500 3000 2500 2000 1500
(1)、求该公司职员月工资的平均数、中位数、众数?
(2)、假设副董事长的工资从5000元 ( http: / / www.21cnjy.com )提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)、你认为应该使用平均数和中位数中哪一个来描述该公司职工的工资水平?
答案:
1.(1).2090 、500、1500; (2).3288、1500、1500
(3)中位数或众数均能反映该公 ( http: / / www.21cnjy.com )司员工的工资水平,因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司员工的工资水平。
四、本节小结
众数是当一组数据中某一数据重复出现较多 ( http: / / www.21cnjy.com )时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,中位数的计算很少也不受极端值的影响.
五、课后作业
(1)课本第146页练习题
(2)课本第147-148页习题第4、7题;
6.2 方差
教学目标
1. 了解方差的定义和计算公式.
2. 理解方差概念的产生和形成的过程.
3. 会用方差计算公式来比较两组数据的波动大小.
教学重点、难点
1.重点:方差产生的必要性和应用方差公式解决实际问题.
2.难点:理解方差公式.
教学过程
一、自主学习
通过预习教材P149~P151的内容,完成下面各题.
1.算一算:甲队的平均身高是__________,乙队的平均身高是_________,单从身高考虑,哪对演出效果好?
2.你准备用什么方法来反映总的偏差的大小?
3.____________________________________________________,称为这组数据的方差.
二、尝试应用
1. 从甲、乙两种农作物中各抽取1株苗,分别测得它的苗高如下:(单位:cm)
甲:9、10、11、12、7、13、10、8、12、8;
乙:8、13、12、11、10、12、7、7、9、11;
问:(1)哪种农作物的苗长的比较高?
(2)哪种农作物的苗长得比较整齐?
2. 段巍和金志强两人参加体育项目训练,近期的5次测试成绩如下表所示,谁的成绩比较稳定?为什么?
测试次数 1 2 3 4 5
段巍 13 14 13 12 13
金志强 10 13 16 14 12
3.课本第151-152页练习题
参考答案:
1.(1)甲、乙两种农作物的苗平均高度相同;(2)甲整齐
2.段巍的成绩比金志强的成绩要稳定.
三、当堂检测
1.已知一组数据为2、0、-1、3、-4,则这组数据的方差为 。
2.甲、乙两名学生在相同的条件下各射靶10次,命中的环数如下:
甲:7、8、6、8、6、5、9、10、7、4
乙:9、5、7、8、7、6、8、6、7、7
经过计算,两人射击环数的平均数相同,但S S,所以确定 去参加比赛。
3. 甲、乙两台机床生产同种零件,10天出的次品分别是( )
甲:0、1、0、2、2、0、3、1、2、4
乙:2、3、1、2、0、2、1、1、2、1
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
4.小爽和小兵在10次百米跑步练习中成绩如表所示:(单位:秒)
小爽 10.8 10.9 11.0 10.7 11.1 11.1 10.8 11.0 10.7 10.9
小兵 10.9 10.9 10.8 10.8 11.0 10.9 10.8 11.1 10.9 10.8
如果根据这几次成绩选拔一人参加比赛,你会选谁呢?
答案:
1. 6; 2. >、乙; 3. =1.5、S=0.975、=1. 5、S=0.425,乙机床性能好.
4. =10.9、S=0.02; =10.9、S=0.008 选择小兵参加比赛.
四、本节小结
1.方差公式:S =[(-)+(-)+…+(-)].
2.从方差公式作分析和解释,波动大小指的是 ( http: / / www.21cnjy.com )与平均数之间差异,那么用每个数据与平均值的差完全平方后便可以反映出每个数据的波动大小,整体的波动大小可以通过对每个数据的波动大小求平均值得到.所以方差公式是能够反映一组数据的波动大小的一个统计量.
五、课后作业
课本第152-153页习题.
第6章 数据分析小结与复习(1)
教学目标
1.描述平均数,中位数,众数的差别,初步感受它们在不同情境中的应用;概述刻画数据波动的统计量:方差.
2.通过小组活动,培养团队精神.通过解决身边的实际问题,初步认识数学与人类生活的密切联系及对人类历史发展的作用.
教学重点、难点
1.重点:平均数、中位数、众数、方差的应用.
2.难点:建立本章知识网络.
教学过程
一、回顾本章主要内容
一般的,对于n个数把叫做这n个数的算术平均数.若n个数中,x1出现f1次,x2出现f2次,…,xk出现fk次,(这里f1+f2+...+fk=n),那么这个公式叫加权平均数公式,其中f1,f2,…,fk叫做权,这个“权”含有所占分量较重之意,fi越大,表示xi个数越多,“权”就越重.
算术平均数是加权平均数的一种特殊情况,加权平均数包括算术平均数,当加权平均数中的权相等时,就是算术平均数.
将一组数据按照由小到大(或由 ( http: / / www.21cnjy.com )大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
中位数是一个位置代表值,利用中位数分析数据可以获得一些信息。如果已知一组数据的中位数,那么可以知道,小于或大于这个中位数的数据各占一半.
众数也常作为一组数据的代表,一组数据中出现次数最多的数据就是这组数据的众数.
如果一组数据中有两个数据出现的次数一样,都是最大,那么这两个数据都是这组数据的众数.
( http: / / www.21cnjy.com )
平均数、中位数、众数的特点
平均数的计算要用到所有的数据,它能够充分利用数据提供的信息,因此,在现在生活中较为常用.但它受极端值的影响较大.
众数:当一组数据中某些数据重复出现时, ( http: / / www.21cnjy.com )众数往往是人们关心的一个量,众数不受极端值的影响,这是它的一个优势,但同时,它又不像平均数那样能充分得用数据提供的信息.
中位数只需要很少的计算,不受极端值的影响,这在有些情况下是一个优点,但它也不能充分利用每个数据所提供的信息.
二、知识结构
三、巩固练习
1. 个体户老王经营一家快餐店,下面是所有员工在某个月的工资情况
人 老王 厨师甲 厨师乙 招待甲 招待乙 勤杂工 会计
月工资 3000 450 400 350 320 320 410
(1)计算快餐店员工这个月的平均工资,中位数、众数.
(2)(1)中的数据是否代表一般员工的月工资收入的一般水平?
(3)去掉老王的工资,再计算其他人的平均工资.
(4)比较(1)与(3)你能发现什么?
解:(1)本店员工的平均工资为:
而中位数为400元;众数为320元.
(2)(1)中的平均数不能代表一般工人的月工资收入的一般水平.因为老王的工资明显很高,而一些工人明显偏低.
(3)去掉老王的工资,再计算其他人的平均工资得
.
(4)比较(1)(3)的平均工资,不难发现在进行数据分析时,平均数往往会受到极端值的影响,而不能体现大多数据的般情况.
平均数、中位数、众数都可以作为一组数据的代表,它们各有自己的特点,能够从不同的角度提供信息.在实际应用中,需要分析具体问题的情况,选择适当的量来代表数据.
2. 某学校初三(一)班甲、乙两名同学参加最近5次数学的成绩(单位:分)统计如下:
甲:65,94,95,98,98; 乙:65,71,98,99,100。
(1)分别写出甲、乙两同学成绩的平均分和中位数;
(2)分别用平均分和中位数解释甲、乙两名同学中谁的成绩较好.
解:(1),甲的中位数是95,乙的中位数是98。
(2)从平均分看,甲的平均分高,甲的成绩较好;从中位数看,乙的成绩好于甲的成绩.
四、当堂检测
课本第156-157页习题第1、2、5题.
五、课后作业
课本第156-157页习题第3、6题.
第6章 数据分析小结与复习(2)
教学目标
1.进一步描述平均数,中位数,众数的差别,初步感受它们在不同情境中的应用;概述刻画数据波动的统计量:方差.
2.进一步通过小组活动,培养团队精神.通过解决身边的实际问题,进一步认识数学与人类生活的密切联系及对人类历史发展的作用.
教学重点、难点
1.重点:平均数、中位数、众数、方差的应用.
2.难点:灵活运用本章知识.
教学过程
一、自主学习
阅读课本第155页对本章知识作进一步回顾.
二、巩固练习
1.如果样本方差,那么这个样本平均数为 .样本容量为 .
2.已知的平均数10,方差3,则的平均数为 ,方差为 .
3.在一次环保知识竞赛中,某班50名学生成绩如下表所示:
得分 50 60 70 80 90 100 110 120
人数 2 3 6 14 15 5 4 1
分别求出这些学生成绩的众数、中位数和平均数.
4. 某养鱼户搞池塘养鱼已三年,头一年 ( http: / / www.21cnjy.com )放养鲢鱼苗20000尾,其成活率约为70%,在秋季捕捞时,捞出10尾鱼,称得每尾鱼的重量如下:(单位:千克)0.8,0.9,1.2,1.3,0.8,0.9,1.1,1.0,1.2,0.8.
(1)根据样本平均数估计这塘鱼的总产量是多少千克
(2)如果把这塘鲢鱼全部卖掉,其市场售价为每千克4元,那么能收人多少元?除去当年的投资成本16000元,第一年纯收入多少元?
解:(1)样本平均数
即每条鲢鱼约重1千克.因此可以估计这塘鲢鱼共重
(2)4×14000=56000(元)56000-16000=40000(元)
所以把鲢鱼全卖掉可收入56000元,除去当年的投资成本纯收入40000元。
选取样本容量的原则:
用样本估计总体时,样本容量越大,样本对总 ( http: / / www.21cnjy.com )体的估计越精确,相应的搜集、整理。计算数据的工作量也越大,因此,在实际工作时,样本容量的确既要考虑问题本身的需要,又要考虑实现的可能性和所付出的代价。
三、当堂检测
1.一组数据:,,0,,1的平均数是0,则= .方差 .
2.样本方差的作用是( )
A.估计总体的平均水平 ; B.表示样本的平均水平;
C.表示总体的波动大小; D.表示样本的波动大小,从而估计总体的波动大小.
3.如果给定数组中每一个数都减去同一非零常数,则数据的( )
A、平均数改变,方差不变 B、平均数改变,方差改变
C、平均数不变,方差不变 D、平均数不变,方差改变
4.甲、乙两名学生在相同的条件下各射靶10次,命中的环数如下:
甲:7,8,6,8,6,5,9,10,7,4 乙:9,5,7,8,7,6,8,6,7,7
经过计算,两人射击环数的平均数相同,但S S,所以确定 去参加比赛.
5.某公司的33名职工的月工资(以元为单位)如下:
职员 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5000 3500 3000 2500 2000 1500
(1)求该公司职员月工资的平均数、中位数、众数?
(2)假设副董事长的工资从5000元提升到2 ( http: / / www.21cnjy.com )0000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)你认为应该使用平均数和中位数中哪一个来描述该公司职工的工资水平?
四、本节小结
1.这节课我们学到了什么知识?
2.我们感受到了什么
3.还存在什么疑惑?
五、课后作业
课本第156-158页习题第4、7、8、9、10题.
165
10
5
身高(cm)
185
175
155
145
15
20
6
10
20
4
人数(人)
台数
规格
月份
离散程度(方差)
6.1 平均数、中位数、众数
6.1.1 平均数(1)
教学目标
使学生掌握平均数的计算方法;
通过本节课的学习,还应使学生理解平均数在 ( http: / / www.21cnjy.com )数据统计中的意义和作用:描述一组数据集中趋势的特征数字,是反映一组数据平均水平的特征数,并认识平均数的优、缺点.
教学重点、难点
1.重点:理解平均数的意义.
2.难点:认识平均数的优、缺点.
教学过程
一、自主学习
通过预习教材P137~P139的内容,完成下面各题.
1.要比较三种棉花哪个品种更好,应比较这三种棉花的___平均结桃数_______.
2.平均数是一组数据的数值的代表值,它刻画了这组数据 整体 平均状态,对于这组数据的 个体性质 不能作什么结论.
3.平均数的缺点是:___容易受个别特殊值的影响_______.
二、尝试应用
1.填空:783,769,774,779,765的平均数是 .
2.填空:在由某电视台举办的唱歌比赛中,由 ( http: / / www.21cnjy.com )10位评委现场给每位歌手打分,然后去掉其中的一个最高分和一个最低分,其余分数的平均数作为该歌手的成绩.已知10位评委给歌手潘多打分是9.5,9.5,9.3,9.8,,9.4,9.1,9.6,9.5,9.2,9.6,则潘多的得分是 (结果保留到小数点后第2位).
3.某班进行了一次数学测验,
第一组的成绩是:56,32,63,74,85,22,44,78,91,65;
第二组的成绩是:46,39,75,83,16,94,66,60,57,72.
请问:哪个组的成绩好?
(答案:因为,第一组平均成绩为==61
第二组平均成绩为==60.8
所以,第一组成绩好些.)
4.若不选择教材中的引入问题,也可以替换成更贴近学生学习生活中的实例,下举一例可供借鉴参考。
某校初二年级共有4个班,在一次数学考试中参考人数和成绩如下:
班级 1班 2班 3班 4班
参考人数 40 42 45 32
平均成绩 80 81 82 79
求该校初二年级在这次数学考试中的平均成绩?下述计算方法是否合理?为什么?
=(79+80+81+82)=80.5
.
三、当堂检测
1.填空:43,50,71,64的平均数是 .
2.填空:一个中学足球队的20名队员的身高如下(单位:厘米):
170,167,171,168,160,1 ( http: / / www.21cnjy.com )72,168,162,172,169,164,174,169,165,175,170,165,167,170,172,则这些队员的平均身高为 厘米.
3.填空:拉萨今年1月上旬各天的最低气温依次是(单位:℃):
-6,-5,-7,-7,-6,-4,-5,-7,-8,-7,则它们的平均气温为 ℃.
4.在“创优”活动中,我市 ( http: / / www.21cnjy.com )某校开展收集废旧电池的活动,该校8年级(1)班为估计4月份收集电池的个数,随机抽取了该月7天收集废旧电池的个数,数据如下:
48,51,53,47,49,50,52.
求这7天该班收集废旧电池的总个数,并估计4月份该班收集废旧电池的个数.
5.个体户张某经营一家餐馆,下面是该餐馆所有工作人员2001年10月份的工资.
张某:4000元;会计:700元;厨师 ( http: / / www.21cnjy.com )甲:1000元;厨师乙:900元;杂工甲:580元;杂工乙:560元;服务员甲:620元;服务员乙:600元;服务员丙:580.
(1)计算他们的平均工资;
(2)不计张某的工资,再求餐馆员工月平均工资.
四、本节小结
平均数计算要用到所有的数据,它能够充分利用所有的数据信息,但它受极端值的影响较大.
五、课后作业
(1)课本第139页练习题
(2)课本第147页习题第1、2题;
6.1.2 平均数(2)
教学目标
1.使学生理解数据的权和加权平均数的概念
2.使学生掌握加权平均数的计算方法
3.会根据加权平均数解决一些实际问题
教学重点、难点
1.重点:会计算加权平均数.
2.难点:对数据权概念的理解.
教学过程
一、自主学习
通过预习教材P139~P141的内容,完成下面各题.
1.填一填:在计算加权平均数时,权 ( http: / / www.21cnjy.com )数可以表示____________________________________:权数之和为_____,权数越大的数据在总体中所占的____________,它对加权平均数的______________.
2.求21、32、43、54分别以0.1、0.2、0.3、0.4为权的加权平均数.
3.在计算加权平均数时,常用________来反映对应的数据的________程度:权数________的数据___________.
二、尝试应用
1.在一次英语口试中,已知50分1 ( http: / / www.21cnjy.com )人、60分2人、70分5人、90分5人、100分1人,其余为84分。已知该班平均成绩为80分,问该班有多少人?
2.一家公司打算招聘一名部门经理,现对甲、乙 ( http: / / www.21cnjy.com )两名应聘者从笔试、面试、实习成绩三个方面表现进行评分,笔试占总成绩20%、面试占30%、实习成绩占50%,各项成绩如表所示:
应聘者 笔试 面试 实习
甲 85 83 90
乙 80 85 92
试判断谁会被公司录取,为什么?
3.某班40名学生身高情况如下图,
请计算该班学生平均身高.(答案: 165.5)
三、当堂检测
1.某人打靶有a次打中环,b次打中环,则此人平均每次中靶 环.
2.老师在计算学期总平均分的时候按如下标准:作业占100%、测验占30%、期中占35%、期末考试占35%,小关和小兵的成绩如下表:
学生 作业 测验 期中考试 期末考试
小关 80 75 71 88
小兵 76 80 68 90
试比较两人谁的成绩好?
四、本节小结
1.这节课我们学到了什么知识?
2.我们感受到了什么
3.还存在什么疑惑?
五、课后作业
(1)课本第142页练习题;
(2)课本第147-148页习题第3、5题.
6.1.2 中位数
教学目标
1.认识中位数,并会求出一组数据中的中位数.
2.理解中位数的意义和作用。它也是数据代表,可以反映一定的数据信息,帮助人们在实际问题中分析并做出决策.
3.会利用中位数分析数据信息做出决策.
教学重点、难点
1.重点:认识中位数这种数据代表.
2.难点:利用中位数分析数据信息做出决策.
教学过程
一、自主学习
通过预习教材P142~P143的内容,完成下面各题.
1.把一组数据___________的顺序排列,如果数据的个数是_____数,那么位于_______的数称为这组数据的中位数.如果数据的个数是_____数,那么位于中间的____个数的平均数称为这组数据的中位数.
2.优点:中位数把一组数 ( http: / / www.21cnjy.com )据分成数目________的两部分,其中一部分_______或_______中位数,而另一部分_______或_______中位数,因此,中位数常用来描述__________________.
3.缺点:它没有利用数据中_________信息,因此,有时它可能不是____________.
二、尝试应用
数据8、9、9、8、10、8、9、8、10、7、9、9、8的中位数是 .
一组数据23、27、20、18、X、12,它的中位数是21,则X的值是 .
3.某公司销售部有营销人员15人,销售部为了制定某种商品的销售金额,统计了这15个人的销售量如下(单位:件)
1800、510、250、250、210、250、210、210、150、210、150、120、120、210、150
求这15个销售员该月销量的中位数.
假设销售部负责人把每位营销员的月销售定额定为320件,你认为合理吗?如果不合理,请你制定一个合理的销售定额并说明理由.
4.随机抽取我市一年(按365天计)中的30天平均气温状况如下表:
温度(℃) -8 -1 7 15 21 24 30
天数 3 5 5 7 6 2 2
请你根据上述数据回答问题:
(1).该组数据的中位数是什么?
(2).若当气温在18℃~25℃为市民“满意温度”,则我市一年中达到市民“满意温度”的大约有多少天?
答案:1. 9; 2. 22; ( http: / / www.21cnjy.com ) 3. (1)210件 (2)不合理。因为15人中有13人的销售额达不到320件(320虽是原始数据的平均数,却不能反映营销人员的一般水平),销售额定为210件合适,因为它既是中位数,是大部分人能达到的额定. 4.(1)15. (2)约97天
三、当堂检测
1.公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄如下:(单位:岁)
甲群:13、13、14、15、15、15、16、17、17.
乙群:3、4、4、5、5、6、6、6、54、57.
(1)、甲群游客的平均年龄是 岁,中位数是 岁,其中能较好反映甲群游客年龄特征的是 。
(2)、乙群游客的平均年龄是 岁,中位数是 岁,其中能较好反映乙群游客年龄特征的是 。
2.某公司有15名员工,它们所在的部门及相应每人所创的年利润如下表示:
部门 A B C D E F G
人数 1 1 2 4 2 2 3
每人所创的年利润 20 5 2.5 2.1 1.5 1.5 1.2
根据表中的信息填空:
该公司每人所创年利润的平均数是 万元。
该公司每人所创年利润的中位数是 万元。
你认为应该使用平均数和中位数中哪一个来描述该公司每人所创年利润的一般水平?答
答案:1.(1)15、15、中位数; (2)15、5.5、中位数.
2.(1)3.2万元 (2)2.1万元 (3)中位数
四、本节小结
中位数仅与数据的排列位置有关,某些数据 ( http: / / www.21cnjy.com )的移动对中位数没有影响,中位数可能出现在所给数据中也可能不在所给的数据中,当一组数据中的个别数据变动较大时,可用中位数描述其趋势.
五、课后作业
(1)课本第144页练习题
(2)课本第148页习题第6题;
6.1.3 众数
教学目标
1.认识众数,并会求出一组数据中的众数.
2.理解众数的意义和作用。它也是数据代表,可以反映一定的数据信息,帮助人们在实际问题中分析并做出决策.
3.会利用众数分析数据信息做出决策.
教学重点、难点
1.重点:认识中位数、众数这两种数据代表.
2.难点:利用中位数、众数分析数据信息做出决策.
教学过程
一、自主学习
通过预习教材P144~P146的内容,完成下面各题.
1.什么是众数?____________________________________________________.
2.自学完例4后,你认为该公司总经理、普通职工以及应聘者将分别关注职工月工资数据的平均数、中位数和众数中的哪一个?为什么
3.思考:众数有什么特点,它的优点 ( http: / / www.21cnjy.com )是什么?缺点是什么?众数是一组数据中的出现次数___________的数,众数可以不止____________.
优点:容易_________,当一组数据中某数多次出现时,可以用众数作为这组数据的数值的_______________.
缺点:众数不能充分利用数据中______________,因此众数不能经常使用.
尝试应用
1.如果在一组数据中,23、25、28、 ( http: / / www.21cnjy.com )22出现的次数依次为2、5、3、4次,并且没有其他的数据,则这组数据的众数和中位数分别是( )
A.24、25 B.23、24 C.25、25 D.23、25
2.数据92、96、98、100、X的众数是96,则其中位数和平均数分别是( )
A.97、96 B.96、96.4 C.96、97 D.98、97
3.某商店3、4月份出售某一品牌各种规格的空调,销售台数如表所示:
1匹 1.2匹 1.5匹 2匹
3月 12台 20台 8台 4台
4月 16台 30台 14台 8台
根据表格回答问题:
商店出售的各种规格空调中,众数是多少?
假如你是经理,现要进货,6月份在有限的资金下进货单位将如何决定?
答案:1.C; 2.B; 3 ( http: / / www.21cnjy.com ).(1)1.2匹 (2)通过观察可知1.2匹的销售最大,所以要多进1.2匹,由于资金有限就要少进2匹空调.
三、当堂检测
1.某公司的33名职工的月工资(以元为单位)如下:
职员 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5000 3500 3000 2500 2000 1500
(1)、求该公司职员月工资的平均数、中位数、众数?
(2)、假设副董事长的工资从5000元 ( http: / / www.21cnjy.com )提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)、你认为应该使用平均数和中位数中哪一个来描述该公司职工的工资水平?
答案:
1.(1).2090 、500、1500; (2).3288、1500、1500
(3)中位数或众数均能反映该公 ( http: / / www.21cnjy.com )司员工的工资水平,因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司员工的工资水平。
四、本节小结
众数是当一组数据中某一数据重复出现较多 ( http: / / www.21cnjy.com )时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,中位数的计算很少也不受极端值的影响.
五、课后作业
(1)课本第146页练习题
(2)课本第147-148页习题第4、7题;
6.2 方差
教学目标
1. 了解方差的定义和计算公式.
2. 理解方差概念的产生和形成的过程.
3. 会用方差计算公式来比较两组数据的波动大小.
教学重点、难点
1.重点:方差产生的必要性和应用方差公式解决实际问题.
2.难点:理解方差公式.
教学过程
一、自主学习
通过预习教材P149~P151的内容,完成下面各题.
1.算一算:甲队的平均身高是__________,乙队的平均身高是_________,单从身高考虑,哪对演出效果好?
2.你准备用什么方法来反映总的偏差的大小?
3.____________________________________________________,称为这组数据的方差.
二、尝试应用
1. 从甲、乙两种农作物中各抽取1株苗,分别测得它的苗高如下:(单位:cm)
甲:9、10、11、12、7、13、10、8、12、8;
乙:8、13、12、11、10、12、7、7、9、11;
问:(1)哪种农作物的苗长的比较高?
(2)哪种农作物的苗长得比较整齐?
2. 段巍和金志强两人参加体育项目训练,近期的5次测试成绩如下表所示,谁的成绩比较稳定?为什么?
测试次数 1 2 3 4 5
段巍 13 14 13 12 13
金志强 10 13 16 14 12
3.课本第151-152页练习题
参考答案:
1.(1)甲、乙两种农作物的苗平均高度相同;(2)甲整齐
2.段巍的成绩比金志强的成绩要稳定.
三、当堂检测
1.已知一组数据为2、0、-1、3、-4,则这组数据的方差为 。
2.甲、乙两名学生在相同的条件下各射靶10次,命中的环数如下:
甲:7、8、6、8、6、5、9、10、7、4
乙:9、5、7、8、7、6、8、6、7、7
经过计算,两人射击环数的平均数相同,但S S,所以确定 去参加比赛。
3. 甲、乙两台机床生产同种零件,10天出的次品分别是( )
甲:0、1、0、2、2、0、3、1、2、4
乙:2、3、1、2、0、2、1、1、2、1
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
4.小爽和小兵在10次百米跑步练习中成绩如表所示:(单位:秒)
小爽 10.8 10.9 11.0 10.7 11.1 11.1 10.8 11.0 10.7 10.9
小兵 10.9 10.9 10.8 10.8 11.0 10.9 10.8 11.1 10.9 10.8
如果根据这几次成绩选拔一人参加比赛,你会选谁呢?
答案:
1. 6; 2. >、乙; 3. =1.5、S=0.975、=1. 5、S=0.425,乙机床性能好.
4. =10.9、S=0.02; =10.9、S=0.008 选择小兵参加比赛.
四、本节小结
1.方差公式:S =[(-)+(-)+…+(-)].
2.从方差公式作分析和解释,波动大小指的是 ( http: / / www.21cnjy.com )与平均数之间差异,那么用每个数据与平均值的差完全平方后便可以反映出每个数据的波动大小,整体的波动大小可以通过对每个数据的波动大小求平均值得到.所以方差公式是能够反映一组数据的波动大小的一个统计量.
五、课后作业
课本第152-153页习题.
第6章 数据分析小结与复习(1)
教学目标
1.描述平均数,中位数,众数的差别,初步感受它们在不同情境中的应用;概述刻画数据波动的统计量:方差.
2.通过小组活动,培养团队精神.通过解决身边的实际问题,初步认识数学与人类生活的密切联系及对人类历史发展的作用.
教学重点、难点
1.重点:平均数、中位数、众数、方差的应用.
2.难点:建立本章知识网络.
教学过程
一、回顾本章主要内容
一般的,对于n个数把叫做这n个数的算术平均数.若n个数中,x1出现f1次,x2出现f2次,…,xk出现fk次,(这里f1+f2+...+fk=n),那么这个公式叫加权平均数公式,其中f1,f2,…,fk叫做权,这个“权”含有所占分量较重之意,fi越大,表示xi个数越多,“权”就越重.
算术平均数是加权平均数的一种特殊情况,加权平均数包括算术平均数,当加权平均数中的权相等时,就是算术平均数.
将一组数据按照由小到大(或由 ( http: / / www.21cnjy.com )大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
中位数是一个位置代表值,利用中位数分析数据可以获得一些信息。如果已知一组数据的中位数,那么可以知道,小于或大于这个中位数的数据各占一半.
众数也常作为一组数据的代表,一组数据中出现次数最多的数据就是这组数据的众数.
如果一组数据中有两个数据出现的次数一样,都是最大,那么这两个数据都是这组数据的众数.
( http: / / www.21cnjy.com )
平均数、中位数、众数的特点
平均数的计算要用到所有的数据,它能够充分利用数据提供的信息,因此,在现在生活中较为常用.但它受极端值的影响较大.
众数:当一组数据中某些数据重复出现时, ( http: / / www.21cnjy.com )众数往往是人们关心的一个量,众数不受极端值的影响,这是它的一个优势,但同时,它又不像平均数那样能充分得用数据提供的信息.
中位数只需要很少的计算,不受极端值的影响,这在有些情况下是一个优点,但它也不能充分利用每个数据所提供的信息.
二、知识结构
三、巩固练习
1. 个体户老王经营一家快餐店,下面是所有员工在某个月的工资情况
人 老王 厨师甲 厨师乙 招待甲 招待乙 勤杂工 会计
月工资 3000 450 400 350 320 320 410
(1)计算快餐店员工这个月的平均工资,中位数、众数.
(2)(1)中的数据是否代表一般员工的月工资收入的一般水平?
(3)去掉老王的工资,再计算其他人的平均工资.
(4)比较(1)与(3)你能发现什么?
解:(1)本店员工的平均工资为:
而中位数为400元;众数为320元.
(2)(1)中的平均数不能代表一般工人的月工资收入的一般水平.因为老王的工资明显很高,而一些工人明显偏低.
(3)去掉老王的工资,再计算其他人的平均工资得
.
(4)比较(1)(3)的平均工资,不难发现在进行数据分析时,平均数往往会受到极端值的影响,而不能体现大多数据的般情况.
平均数、中位数、众数都可以作为一组数据的代表,它们各有自己的特点,能够从不同的角度提供信息.在实际应用中,需要分析具体问题的情况,选择适当的量来代表数据.
2. 某学校初三(一)班甲、乙两名同学参加最近5次数学的成绩(单位:分)统计如下:
甲:65,94,95,98,98; 乙:65,71,98,99,100。
(1)分别写出甲、乙两同学成绩的平均分和中位数;
(2)分别用平均分和中位数解释甲、乙两名同学中谁的成绩较好.
解:(1),甲的中位数是95,乙的中位数是98。
(2)从平均分看,甲的平均分高,甲的成绩较好;从中位数看,乙的成绩好于甲的成绩.
四、当堂检测
课本第156-157页习题第1、2、5题.
五、课后作业
课本第156-157页习题第3、6题.
第6章 数据分析小结与复习(2)
教学目标
1.进一步描述平均数,中位数,众数的差别,初步感受它们在不同情境中的应用;概述刻画数据波动的统计量:方差.
2.进一步通过小组活动,培养团队精神.通过解决身边的实际问题,进一步认识数学与人类生活的密切联系及对人类历史发展的作用.
教学重点、难点
1.重点:平均数、中位数、众数、方差的应用.
2.难点:灵活运用本章知识.
教学过程
一、自主学习
阅读课本第155页对本章知识作进一步回顾.
二、巩固练习
1.如果样本方差,那么这个样本平均数为 .样本容量为 .
2.已知的平均数10,方差3,则的平均数为 ,方差为 .
3.在一次环保知识竞赛中,某班50名学生成绩如下表所示:
得分 50 60 70 80 90 100 110 120
人数 2 3 6 14 15 5 4 1
分别求出这些学生成绩的众数、中位数和平均数.
4. 某养鱼户搞池塘养鱼已三年,头一年 ( http: / / www.21cnjy.com )放养鲢鱼苗20000尾,其成活率约为70%,在秋季捕捞时,捞出10尾鱼,称得每尾鱼的重量如下:(单位:千克)0.8,0.9,1.2,1.3,0.8,0.9,1.1,1.0,1.2,0.8.
(1)根据样本平均数估计这塘鱼的总产量是多少千克
(2)如果把这塘鲢鱼全部卖掉,其市场售价为每千克4元,那么能收人多少元?除去当年的投资成本16000元,第一年纯收入多少元?
解:(1)样本平均数
即每条鲢鱼约重1千克.因此可以估计这塘鲢鱼共重
(2)4×14000=56000(元)56000-16000=40000(元)
所以把鲢鱼全卖掉可收入56000元,除去当年的投资成本纯收入40000元。
选取样本容量的原则:
用样本估计总体时,样本容量越大,样本对总 ( http: / / www.21cnjy.com )体的估计越精确,相应的搜集、整理。计算数据的工作量也越大,因此,在实际工作时,样本容量的确既要考虑问题本身的需要,又要考虑实现的可能性和所付出的代价。
三、当堂检测
1.一组数据:,,0,,1的平均数是0,则= .方差 .
2.样本方差的作用是( )
A.估计总体的平均水平 ; B.表示样本的平均水平;
C.表示总体的波动大小; D.表示样本的波动大小,从而估计总体的波动大小.
3.如果给定数组中每一个数都减去同一非零常数,则数据的( )
A、平均数改变,方差不变 B、平均数改变,方差改变
C、平均数不变,方差不变 D、平均数不变,方差改变
4.甲、乙两名学生在相同的条件下各射靶10次,命中的环数如下:
甲:7,8,6,8,6,5,9,10,7,4 乙:9,5,7,8,7,6,8,6,7,7
经过计算,两人射击环数的平均数相同,但S S,所以确定 去参加比赛.
5.某公司的33名职工的月工资(以元为单位)如下:
职员 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5000 3500 3000 2500 2000 1500
(1)求该公司职员月工资的平均数、中位数、众数?
(2)假设副董事长的工资从5000元提升到2 ( http: / / www.21cnjy.com )0000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)你认为应该使用平均数和中位数中哪一个来描述该公司职工的工资水平?
四、本节小结
1.这节课我们学到了什么知识?
2.我们感受到了什么
3.还存在什么疑惑?
五、课后作业
课本第156-158页习题第4、7、8、9、10题.
165
10
5
身高(cm)
185
175
155
145
15
20
6
10
20
4
人数(人)
台数
规格
月份
离散程度(方差)
