图形的旋转
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第二十三章 旋转
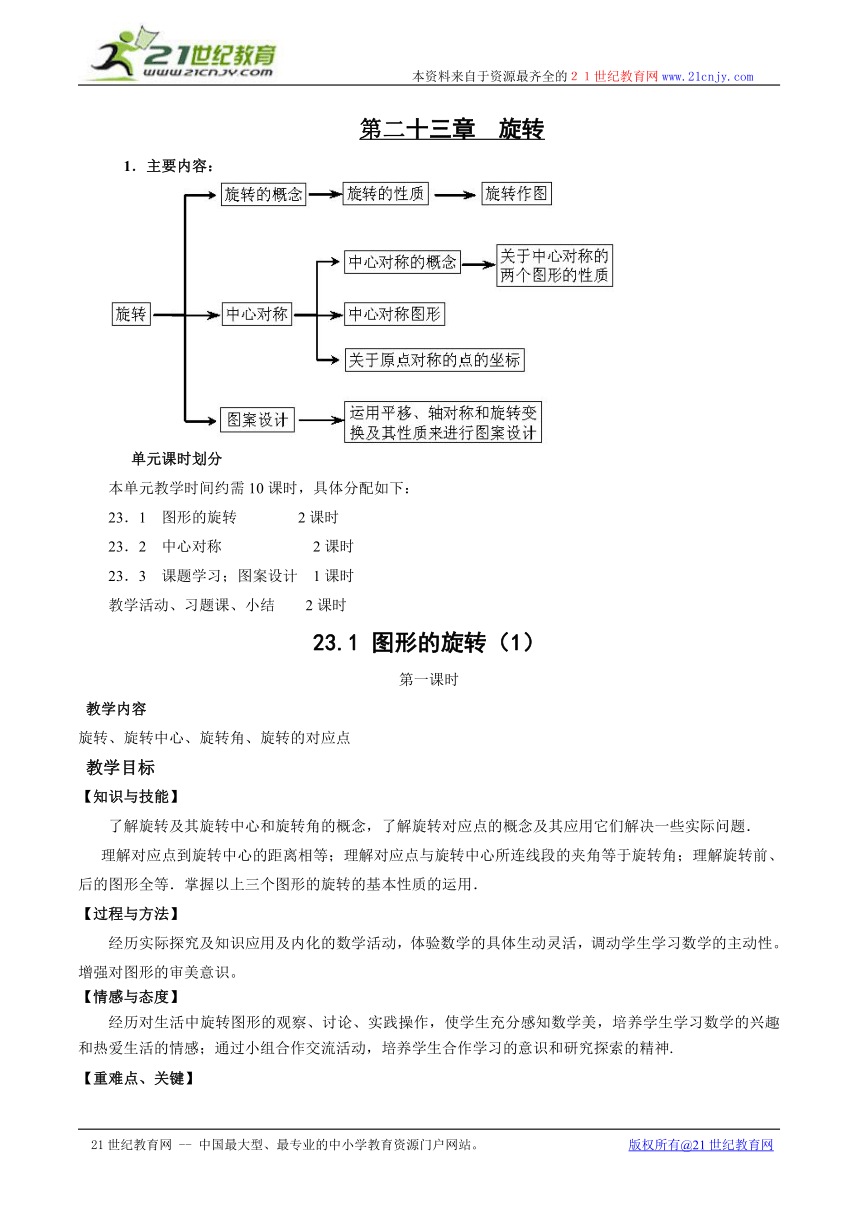
1.主要内容:
单元课时划分
本单元教学时间约需10课时,具体分配如下:
23.1 图形的旋转 2课时
23.2 中心对称 2课时
23.3 课题学习;图案设计 1课时
教学活动、习题课、小结 2课时
23.1 图形的旋转(1)
第一课时
教学内容
旋转、旋转中心、旋转角、旋转的对应点
教学目标
【知识与技能】
了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念及其应用它们解决一些实际问题.
理解对应点到旋转中心的距离相等;理解对应点与旋转中心所连线段的夹角等于旋转角;理解旋转前、后的图形全等.掌握以上三个图形的旋转的基本性质的运用.
【过程与方法】
经历实际探究及知识应用及内化的数学活动,体验数学的具体生动灵活,调动学生学习数学的主动性。增强对图形的审美意识。
【情感与态度】
经历对生活中旋转图形的观察、讨论、实践操作,使学生充分感知数学美,培养学生学习数学的兴趣 ( http: / / )和热爱生活的情感;通过小组合作交流活动,培养学生合作学习的意识和研究探索的精神.
【重难点、关键】
重点:对生活中的旋转现象作数学分析,认识旋转的有关概念和旋转的基本性质
难点:探索旋转后的现象,探索旋转的基本性质
【教学过程】
(一)、创设情境 导入新课
1、日常生活中,经常看到以下情境:游乐场里的摩天轮绕着一个固定的点旋转;钟摆绕着一个固定的点摆动。。。。。。(有条件的学校可以用实物投影仪投放生活中的旋转实例)
提出问题:⑴上述情境中的旋转现象有什么共同的特征?
⑵生活还有类似的例子吗?
日常生活中部分物体的旋转现象.
时钟上的指针不停转动,风车的风轮随风舞动,飞转的电风扇带来丝丝凉意,秋千高高荡起 ……
(二)、合作交流,解读探究
1、旋转的有关概念
观察:时钟上分针的运动.
问题:时钟上分针的转动是绕哪一个点转动?沿着什么方向转动?从5分到15分转动了多少角度.?
定义:把一个图形绕着某一个点O转动一个角度的图形变换叫做旋转,点O叫旋转中心,转动的角叫旋转角. 如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点。
提示:⑴“将一个图形绕着一个定点旋转一定的角度”意味着图形上的每一点同时都按相同的方式旋转相同的角度;
⑵与平移的情况相同,“图形的旋转不改变图形的形状、大小”,
(3)图形的旋转由旋转中心和旋转角度决定
练习;教材P63 练习1、2、3
例1 将一块三角尺ABC绕点C按逆时针方向旋转到△DEC的位置
(1)其中点A 转到了哪个位置?点B、C呢?
象点A和点D,点B和点E,点C和点C这样的点称为对应点,
类似的,图中还有对应线段,对应角,指出它们。
(2)在这个旋转过程中,旋转中心是什么?旋转角是什么?
2、旋转的性质
(3)度量∠ACD与∠BCE的度数,线段AC与DC、BC与EC的长度。你发现了什么?
①距离相等,②夹角相等,③前后图形全等
(4)让学生讨论:三角形在旋转过程中哪些发生了改变?哪些没有发生改变?通过学生的讨论得出旋转的性质:
旋转前、后的图形全等。
对应点到旋转中心的距离相等。
每一对对应点与旋转中心的连线所成的角彼此相等。
那么这个是否有一般性?下面请看这个实验.
在硬纸板上挖下一个三角形的洞,再挖一个点O作为旋转中心,把挖好的硬纸板放在黑板上,先在黑板上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心O转动硬纸板,在黑板上再描出这个挖掉的三角形(△A′B′C′),移去硬纸板.
(分组讨论)根据图回答下面问题(一组推荐一人上台说明)
1.指出图中的对应点,对应线段,对应角
2线段OA与OA′,OB与OB′,OC与OC′有什么关系?
3.∠AOA′,∠BOB′,∠COC′有什么关系?
4.△ABC与△A′B′C′形状和大小有什么关系?
老师点评:1.OA=OA′,OB=OB′,OC=OC′,也就是对应点到旋转中心相等.
2.∠AOA′=∠BOB′=∠COC′,我们把这三个相等的角,即对应点与旋转中心所连线段的夹角称为旋转角.
3.△ABC和△A′B′C′形状相同和大小相等,即全等.
综合以上的实验操作,验证了前面的结论
3、分析旋转现象,画出旋转图形
如图,四边形ABCD是正方形,E是CD上任意一点,以A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。
变式:1、改为△ADE逆时针旋转90°来绘图
2、四边形ABCD是边长为1的正方形,E在CD上且DE=,△ABF是△ADE的旋转图形.
(1)旋转中心是哪一点?(2)旋转了多少度?
(3)AF的长度是多少? (4)如果连结EF,那么△AEF是怎样的三角形?
(三)应用迁移,巩固提高
.1、如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是__________.
2、如图,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是________;(2)旋转角度是________;(3)△ADP是________三角形.
3、如图,将△ABC绕点C按逆时针方向旋转30°点B落在
B′位置,点A落在A′位置,若AC⊥AB,求∠B′A′C
4、如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边
A′B′上,直角边CA′交AB于D,则旋转角等于( ).
A.70° B.80° C.60° D.50°
(四)、应用拓展
两个边长为1的正方形,如图所示,让一个正方形的顶点与另一个正方形中心重合,不难知道重合部分的面积为,现把其中一个正方形固定不动,另一个正方形绕其中心旋转,问在旋转过程中,两个正方形重叠部分面积是否发生变化?说明理由.
(五)、归纳小结(学生总结,老师点评)
本节课要掌握:
1.旋转及其旋转中心、旋转角的概念.
2.旋转的对应点及其它们的应用.
(六)、布置作业
1.活页练习47
2.一块等边三角形木块,边长为1,如图,现将木块沿水平线翻滚五个三角形,那么B点从开始至结束所走过的路径长是多少?
( http: / / )
课后反思
A
C
D
B
E
B′
B
A
C
A′
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第二十三章 旋转
1.主要内容:
单元课时划分
本单元教学时间约需10课时,具体分配如下:
23.1 图形的旋转 2课时
23.2 中心对称 2课时
23.3 课题学习;图案设计 1课时
教学活动、习题课、小结 2课时
23.1 图形的旋转(1)
第一课时
教学内容
旋转、旋转中心、旋转角、旋转的对应点
教学目标
【知识与技能】
了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念及其应用它们解决一些实际问题.
理解对应点到旋转中心的距离相等;理解对应点与旋转中心所连线段的夹角等于旋转角;理解旋转前、后的图形全等.掌握以上三个图形的旋转的基本性质的运用.
【过程与方法】
经历实际探究及知识应用及内化的数学活动,体验数学的具体生动灵活,调动学生学习数学的主动性。增强对图形的审美意识。
【情感与态度】
经历对生活中旋转图形的观察、讨论、实践操作,使学生充分感知数学美,培养学生学习数学的兴趣 ( http: / / )和热爱生活的情感;通过小组合作交流活动,培养学生合作学习的意识和研究探索的精神.
【重难点、关键】
重点:对生活中的旋转现象作数学分析,认识旋转的有关概念和旋转的基本性质
难点:探索旋转后的现象,探索旋转的基本性质
【教学过程】
(一)、创设情境 导入新课
1、日常生活中,经常看到以下情境:游乐场里的摩天轮绕着一个固定的点旋转;钟摆绕着一个固定的点摆动。。。。。。(有条件的学校可以用实物投影仪投放生活中的旋转实例)
提出问题:⑴上述情境中的旋转现象有什么共同的特征?
⑵生活还有类似的例子吗?
日常生活中部分物体的旋转现象.
时钟上的指针不停转动,风车的风轮随风舞动,飞转的电风扇带来丝丝凉意,秋千高高荡起 ……
(二)、合作交流,解读探究
1、旋转的有关概念
观察:时钟上分针的运动.
问题:时钟上分针的转动是绕哪一个点转动?沿着什么方向转动?从5分到15分转动了多少角度.?
定义:把一个图形绕着某一个点O转动一个角度的图形变换叫做旋转,点O叫旋转中心,转动的角叫旋转角. 如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点。
提示:⑴“将一个图形绕着一个定点旋转一定的角度”意味着图形上的每一点同时都按相同的方式旋转相同的角度;
⑵与平移的情况相同,“图形的旋转不改变图形的形状、大小”,
(3)图形的旋转由旋转中心和旋转角度决定
练习;教材P63 练习1、2、3
例1 将一块三角尺ABC绕点C按逆时针方向旋转到△DEC的位置
(1)其中点A 转到了哪个位置?点B、C呢?
象点A和点D,点B和点E,点C和点C这样的点称为对应点,
类似的,图中还有对应线段,对应角,指出它们。
(2)在这个旋转过程中,旋转中心是什么?旋转角是什么?
2、旋转的性质
(3)度量∠ACD与∠BCE的度数,线段AC与DC、BC与EC的长度。你发现了什么?
①距离相等,②夹角相等,③前后图形全等
(4)让学生讨论:三角形在旋转过程中哪些发生了改变?哪些没有发生改变?通过学生的讨论得出旋转的性质:
旋转前、后的图形全等。
对应点到旋转中心的距离相等。
每一对对应点与旋转中心的连线所成的角彼此相等。
那么这个是否有一般性?下面请看这个实验.
在硬纸板上挖下一个三角形的洞,再挖一个点O作为旋转中心,把挖好的硬纸板放在黑板上,先在黑板上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心O转动硬纸板,在黑板上再描出这个挖掉的三角形(△A′B′C′),移去硬纸板.
(分组讨论)根据图回答下面问题(一组推荐一人上台说明)
1.指出图中的对应点,对应线段,对应角
2线段OA与OA′,OB与OB′,OC与OC′有什么关系?
3.∠AOA′,∠BOB′,∠COC′有什么关系?
4.△ABC与△A′B′C′形状和大小有什么关系?
老师点评:1.OA=OA′,OB=OB′,OC=OC′,也就是对应点到旋转中心相等.
2.∠AOA′=∠BOB′=∠COC′,我们把这三个相等的角,即对应点与旋转中心所连线段的夹角称为旋转角.
3.△ABC和△A′B′C′形状相同和大小相等,即全等.
综合以上的实验操作,验证了前面的结论
3、分析旋转现象,画出旋转图形
如图,四边形ABCD是正方形,E是CD上任意一点,以A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。
变式:1、改为△ADE逆时针旋转90°来绘图
2、四边形ABCD是边长为1的正方形,E在CD上且DE=,△ABF是△ADE的旋转图形.
(1)旋转中心是哪一点?(2)旋转了多少度?
(3)AF的长度是多少? (4)如果连结EF,那么△AEF是怎样的三角形?
(三)应用迁移,巩固提高
.1、如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是__________.
2、如图,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是________;(2)旋转角度是________;(3)△ADP是________三角形.
3、如图,将△ABC绕点C按逆时针方向旋转30°点B落在
B′位置,点A落在A′位置,若AC⊥AB,求∠B′A′C
4、如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边
A′B′上,直角边CA′交AB于D,则旋转角等于( ).
A.70° B.80° C.60° D.50°
(四)、应用拓展
两个边长为1的正方形,如图所示,让一个正方形的顶点与另一个正方形中心重合,不难知道重合部分的面积为,现把其中一个正方形固定不动,另一个正方形绕其中心旋转,问在旋转过程中,两个正方形重叠部分面积是否发生变化?说明理由.
(五)、归纳小结(学生总结,老师点评)
本节课要掌握:
1.旋转及其旋转中心、旋转角的概念.
2.旋转的对应点及其它们的应用.
(六)、布置作业
1.活页练习47
2.一块等边三角形木块,边长为1,如图,现将木块沿水平线翻滚五个三角形,那么B点从开始至结束所走过的路径长是多少?
( http: / / )
课后反思
A
C
D
B
E
B′
B
A
C
A′
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
