人教版数学9年级上册第25单元测试(含答案)
文档属性
| 名称 | 人教版数学9年级上册第25单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 436.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 12:41:36 | ||
图片预览




文档简介
人教版数学9年级上册
第25单元测试
时间:90分钟 满分:100分
班级__________姓名__________得分__________
一、选择题(共12小题,满分36分,每小题3分)
1.(3分)(2022 宁夏)下列事件为确定事件的有( )
(1)打开电视正在播动画片
(2)长、宽为m,n的矩形面积是mn
(3)掷一枚质地均匀的硬币,正面朝上
(4)π是无理数
A.1个 B.2个 C.3个 D.4个
2.(3分)(2022 南京模拟)将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )
A. B. C. D.
3.(3分)(2022秋 海曙区期中)布袋中有红、白、绿三种只有颜色不同的球各一个,从中先摸出一个球,记录下它的颜色,将它放回布袋并搅匀,再摸出一个球,记录下颜色.则摸出的两个球颜色为“一白一绿”的概率是( )
A. B. C. D.
4.(3分)(2022秋 顺德区期中)将4张分别写着“强”“国”“有”“我”的卡片(卡片的形状、大小、质地都相同)放在盒子中,搅匀后从中随机取出2张卡片,则取出的2张卡片中,恰好组成“强国”的概率为( )
A. B. C. D.
5.(3分)(2022秋 衢江区校级月考)已知M(a,b)是平面直角坐标系xOy中的点,其中a是从1,2,3三个数中任取的一个数,b是从1,2,3,4四个数中任取的一个数.定义“点M(a,b)在直线x+y=n上”为事件Qn(2≤n≤7,n为整数),则当Qn的概率最大时,n的所有可能的值为( )
A.5 B.4或5 C.5或6 D.4或6
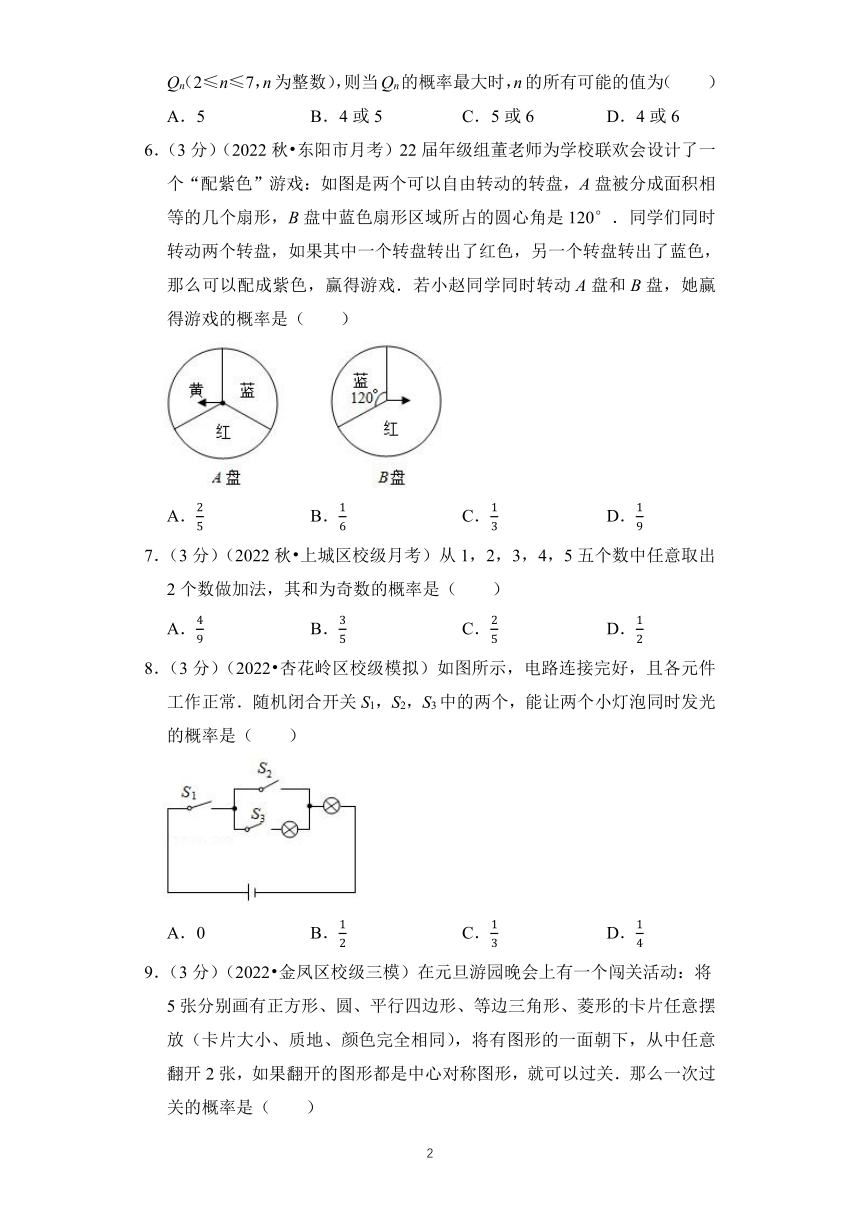
6.(3分)(2022秋 东阳市月考)22届年级组董老师为学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小赵同学同时转动A盘和B盘,她赢得游戏的概率是( )
A. B. C. D.
7.(3分)(2022秋 上城区校级月考)从1,2,3,4,5五个数中任意取出2个数做加法,其和为奇数的概率是( )
A. B. C. D.
8.(3分)(2022 杏花岭区校级模拟)如图所示,电路连接完好,且各元件工作正常.随机闭合开关S1,S2,S3中的两个,能让两个小灯泡同时发光的概率是( )
A.0 B. C. D.
9.(3分)(2022 金凤区校级三模)在元旦游园晚会上有一个闯关活动:将5张分别画有正方形、圆、平行四边形、等边三角形、菱形的卡片任意摆放(卡片大小、质地、颜色完全相同),将有图形的一面朝下,从中任意翻开2张,如果翻开的图形都是中心对称图形,就可以过关.那么一次过关的概率是( )
A. B. C. D.
10.(3分)(2022 肥东县校级模拟)如图,湖边建有A,B,C,D共4座凉亭,某同学计划将这4座凉亭全部参观一遍,从入口处进,先经过凉亭A,接下来参观凉亭B或凉亭C(已经参观过的凉亭,再次经过时不作停留),则最后一次参观的凉亭为凉亭D的概率为( )
A. B. C. D.
11.(3分)(2022 思明区校级二模)厦门在形式上助手数学社团的同学做了估算π的实验.方法如下:
第一步:请全校同学随意写出两个实数x、y(x、y可以相等),且它们满足:0<x<1,0<y<1;
第二步:统计收集上来的有效数据,设“以x,y,1为三条边长能构成锐角三角形”为事件A;
第三步:计算事件A发生的概率,及收集的本校有效数据中事件A出现的频率;
第四步:估算出π的值.
为了计算事件A的概率,同学们通过查阅资料得到以下两条信息:
①如果一次试验中,结果落在区域D中每一个点都是等可能的,用A表示“试验结果落在区域D中一个小区域M中”这个事件,那么事件A发生的概率为P(A);
②若x,y,1三个数据能构成锐角三角形,则需满足x2+y2>1.
根据上述材料,社团的同学们画出图,若共搜集上来的m份数据中能和“1”构成锐角三角形的数据有n份,则可以估计π的值为( )
A. B. C. D.
12.(3分)(2022 费县二模)为了方便市民就近采集核酸,我市最近增设了一批核酸采样点,争取让市民步行15分钟之内就能找到核酸采样点,甲、乙两人各自随机选择到A,B两个新冠病毒核酸检测点进行核酸检测.这两人都在A检测点进行检测的概率是( )
A. B. C. D.
二、填空题(共6小题,满分18分,每小题3分)
13.(3分)(2022秋 迎泽区校级月考)有4张卡片(形状、大小、质地都相同),上面分别画有下列图形:①平行四边形;②菱形;③矩形;④正方形;将卡片背面朝上洗匀,从中抽取一张,正面图形既是轴对称图形,又是中心对称图形的概率是 .
14.(3分)(2022秋 金牛区校级月考)从2,0,﹣1,﹣2,﹣3这五个数中,随机抽取一个数作为m的值,则使函数y=(m+3)x的图象经过第一、三象限,且使关于x的一元二次方程(m﹣1)x2﹣(2m﹣1)x+m+2=0有实数根的概率是 .
15.(3分)(2022秋 姜堰区期中)如图,飞镖游戏板中每一块小正方形除颜色外都相同.假设飞镖击中每一块小正方形是等可能的(击中小正方形边界或没有击中游戏板,则重投掷一次),任意投掷飞镖1次,则飞镖击中阴影部分的概率是 .
16.(3分)(2022秋 龙岗区校级月考)学校团委在“五四青年节”举行“感动校园十大人物”颁奖活动中,九(4)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动,则甲乙两人恰有一人参加此活动的概率是 .
17.(3分)(2022秋 袁州区校级月考)袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为”,则这个袋中白球大约有 个.
18.(3分)(2022秋 忠县校级月考)一个不透明的口袋中有4个完全相同的小球,球上分别标有数字﹣2,0,1,4.随机摸出一个小球记作m,然后放回,再随机摸出一个小球记作n,则方程mx2﹣2x+n=0是关于x的一元二次方程且此方程无解的概率为 .
三、解答题(共7小题,满分66分)
19.(8分)(2022秋 桐庐县期中)王璐老师为幼儿园小朋友,设计了A,B,C三种款式的围巾和甲,乙两种款式的帽子,供小朋友挑选任一款围巾和一款帽子进行搭配.
(1)用列表或者树状图表示所有搭配可能的结果.
(2)求某个小朋友搭配A款围巾和乙款帽子的概率.
20.(8分)(2022秋 鲤城区校级期中)电子政务、数字经济、智慧社会一场数字革命正在神州大地激荡.某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成统计图表(不完整):请观察下面的图表,解答下列问题:
组别 成绩 人数
A 60≤x<70 10
B 70≤x<80 m
C 80≤x<90 16
D 90≤x<100 4
(1)统计表中m= ;统计图中n= ,D组圆心角的度数是 .
(2)D组的4名学生中,有2名男生和2名女生从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求至少1名女生被抽取参加5G体验活动的概率.
21.(8分)(2022秋 法库县期中)不透明布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出一个球.
(1)第二次摸出白球的概率是多少?(直接写出结论)
(2)请用表格或树状图求出两次都摸出白球的概率.
22.(8分)(2022秋 西湖区校级期中)有四张背面完全相同的纸牌A,B,C,D,其中正面分别写着不同的度数,小华将这四张纸牌背面朝上洗匀后先随机抽出一张(不放回),再随机抽出一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A,B,C,D表示);
(2)求摸出两张纸牌牌面上所写角度恰是互补的概率.
23.(8分)(2022秋 淳安县期中)一个不透明的袋中装有18个红球和若干个白球,它们除颜色外其他均相同.已知将袋中球摇匀后,从中任意摸出一个球是红球的概率是.
(1)求袋中总共有多少个球?
(2)从袋中取走25个球(其中15个红球,10个白球)并将袋中球摇匀后,从剩余的球中任意摸出两个球,求摸出的球是一红一白的概率.
24.(13分)(2022秋 西湖区校级期中)初三年级“黄金分割项目活动”展示,为了解全体初三年级同学的活动成绩,抽取了部分参加活动的同学的成绩进行统计后,分为“优秀”,“良好”,“一般”,“较差”四个等级,并根据成绩绘制成如图两幅不完整的统计图,请结合统计图中的信息,回答下列问题:
(1)扇形统计图中“优秀”所对应扇形的圆心角为 度,并将条形统计图补充完整.
(2)如果学校初三年级共有340名学生,则参加“黄金分割项目活动”比赛成绩良好的学生有 人.
(3)此次活动中有四名同学获得满分,分别是甲,乙,丙,丁,现从这四名同学中挑选两名同学参加校外举行的“黄金分割项目活动”展示,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
25.(13分)(2022秋 锦江区校级期中)成都某中学为了解九年级学生的体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了 名学生,并补全条形图.
(2)“C等级”在扇形图中的圆心角度数为 .
(3)若该中学九年级共有700名学生,请你估计该中学九年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,作为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.
参考答案
一、选择题(共12小题,满分36分,每小题3分)
1.B; 2.A; 3.D; 4.C; 5.B; 6.C; 7.B; 8.C; 9.C; 10.C; 11.D; 12.C;
二、填空题(共6小题,满分18分,每小题3分)
13.
14.
15.
16.
17.3
18.;
三、解答题(共7小题,满分66分)
19.解:(1)画树状图如下:
所有搭配可能的结果有6种;
(2)由(1)可知,所有搭配等可能的结果有6种,其中某个小朋友搭配A款围巾和乙款帽子的结果有1种,
∴某个小朋友搭配A款围巾和乙款帽子的概率为.
20.解:(1)该校八年级参加竞赛的学生人数为:10÷20%=50(人),
∴m=50﹣10﹣16﹣4=20,
n%=16÷50×100%=32%,
∴n=32,
D组的圆心角为:360°28.8°,
故答案为:20,32,28.8°;
(2)画树状图如下:
共有12种等可能的结果,其中至少1名女生被抽取参加5G体验活动的结果有10种,
∴至少1名女生被抽取参加5G体验活动的概率为.
21.解:(1)第二次摸出白球的概率是;
(2)画树状图如下:
共有9种等可能的结果,其中两次都摸出白球的有4种结果,
∴两次都摸出白球的概率为.
22.解:(1)画树状图如下:
两次摸牌所有可能出现的结果共有12种;
(2)由(1)可知,共有12种等可能的结果,其中摸出两张纸牌牌面上所写角度恰是互补的结果有2种,即BD、DB,
∴摸出两张纸牌牌面上所写角度恰是互补的概率为.
23.解:(1)设袋中共有x个球,
∵袋中装有18个红球,从中任意摸出一个球是红球的概率是,
∴,
解得:x=30,
经检验,x=30是原方程的解,
答:袋中总共有30个球.
(2)袋子中白球的个数为:30﹣18=12(个),
取走取走25个球(其中15个红球,10个白球),
则袋子中球的总个数为30﹣25=5(个),红球的个数为:18﹣15=3(个),白球的个数为:12﹣10=2(个),
画树状图如下:
共有20种等可能的结果,其中摸出的球是一红一白的结果有12种,
∴摸出的球是一红一白的概率为.
24.解:(1)抽取的学生人数为:18÷15%=120(人),
∴扇形统计图中“优秀”所对应扇形的圆心角为:360°72°,
∴“良好”等级的人数为120×40%=48(人),
故答案为:72,
把条形统计图补充完整如下:
(2)320×40%=128(人),
∴参加“黄金分割项目活动”比赛成绩良好的学生有128人;
故答案为:128;
(3)画树状图如下:
共有12种等可能的结果,其中选中的两名同学恰好是甲、丁的结果有2种,
∴选中的两名同学恰好是甲、丁的概率.
25.解:(1)10÷20%=50,
所以本次抽样调查共抽取了50名学生;
(2)测试结果为C等级的学生数为50﹣10﹣20﹣4=16(人);
360°115.2°,
(3)70056(名),
所以估计该中学八年级学生中体能测试结果为D等级的学生有56名;
(4)用列表法表示所有可能出现的结果如下:
共有12种等可能的结果数,其中抽取的两人恰好都是男生的结果数为2,
所以抽取的两人恰好都是男生的概率.
10
第25单元测试
时间:90分钟 满分:100分
班级__________姓名__________得分__________
一、选择题(共12小题,满分36分,每小题3分)
1.(3分)(2022 宁夏)下列事件为确定事件的有( )
(1)打开电视正在播动画片
(2)长、宽为m,n的矩形面积是mn
(3)掷一枚质地均匀的硬币,正面朝上
(4)π是无理数
A.1个 B.2个 C.3个 D.4个
2.(3分)(2022 南京模拟)将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )
A. B. C. D.
3.(3分)(2022秋 海曙区期中)布袋中有红、白、绿三种只有颜色不同的球各一个,从中先摸出一个球,记录下它的颜色,将它放回布袋并搅匀,再摸出一个球,记录下颜色.则摸出的两个球颜色为“一白一绿”的概率是( )
A. B. C. D.
4.(3分)(2022秋 顺德区期中)将4张分别写着“强”“国”“有”“我”的卡片(卡片的形状、大小、质地都相同)放在盒子中,搅匀后从中随机取出2张卡片,则取出的2张卡片中,恰好组成“强国”的概率为( )
A. B. C. D.
5.(3分)(2022秋 衢江区校级月考)已知M(a,b)是平面直角坐标系xOy中的点,其中a是从1,2,3三个数中任取的一个数,b是从1,2,3,4四个数中任取的一个数.定义“点M(a,b)在直线x+y=n上”为事件Qn(2≤n≤7,n为整数),则当Qn的概率最大时,n的所有可能的值为( )
A.5 B.4或5 C.5或6 D.4或6
6.(3分)(2022秋 东阳市月考)22届年级组董老师为学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小赵同学同时转动A盘和B盘,她赢得游戏的概率是( )
A. B. C. D.
7.(3分)(2022秋 上城区校级月考)从1,2,3,4,5五个数中任意取出2个数做加法,其和为奇数的概率是( )
A. B. C. D.
8.(3分)(2022 杏花岭区校级模拟)如图所示,电路连接完好,且各元件工作正常.随机闭合开关S1,S2,S3中的两个,能让两个小灯泡同时发光的概率是( )
A.0 B. C. D.
9.(3分)(2022 金凤区校级三模)在元旦游园晚会上有一个闯关活动:将5张分别画有正方形、圆、平行四边形、等边三角形、菱形的卡片任意摆放(卡片大小、质地、颜色完全相同),将有图形的一面朝下,从中任意翻开2张,如果翻开的图形都是中心对称图形,就可以过关.那么一次过关的概率是( )
A. B. C. D.
10.(3分)(2022 肥东县校级模拟)如图,湖边建有A,B,C,D共4座凉亭,某同学计划将这4座凉亭全部参观一遍,从入口处进,先经过凉亭A,接下来参观凉亭B或凉亭C(已经参观过的凉亭,再次经过时不作停留),则最后一次参观的凉亭为凉亭D的概率为( )
A. B. C. D.
11.(3分)(2022 思明区校级二模)厦门在形式上助手数学社团的同学做了估算π的实验.方法如下:
第一步:请全校同学随意写出两个实数x、y(x、y可以相等),且它们满足:0<x<1,0<y<1;
第二步:统计收集上来的有效数据,设“以x,y,1为三条边长能构成锐角三角形”为事件A;
第三步:计算事件A发生的概率,及收集的本校有效数据中事件A出现的频率;
第四步:估算出π的值.
为了计算事件A的概率,同学们通过查阅资料得到以下两条信息:
①如果一次试验中,结果落在区域D中每一个点都是等可能的,用A表示“试验结果落在区域D中一个小区域M中”这个事件,那么事件A发生的概率为P(A);
②若x,y,1三个数据能构成锐角三角形,则需满足x2+y2>1.
根据上述材料,社团的同学们画出图,若共搜集上来的m份数据中能和“1”构成锐角三角形的数据有n份,则可以估计π的值为( )
A. B. C. D.
12.(3分)(2022 费县二模)为了方便市民就近采集核酸,我市最近增设了一批核酸采样点,争取让市民步行15分钟之内就能找到核酸采样点,甲、乙两人各自随机选择到A,B两个新冠病毒核酸检测点进行核酸检测.这两人都在A检测点进行检测的概率是( )
A. B. C. D.
二、填空题(共6小题,满分18分,每小题3分)
13.(3分)(2022秋 迎泽区校级月考)有4张卡片(形状、大小、质地都相同),上面分别画有下列图形:①平行四边形;②菱形;③矩形;④正方形;将卡片背面朝上洗匀,从中抽取一张,正面图形既是轴对称图形,又是中心对称图形的概率是 .
14.(3分)(2022秋 金牛区校级月考)从2,0,﹣1,﹣2,﹣3这五个数中,随机抽取一个数作为m的值,则使函数y=(m+3)x的图象经过第一、三象限,且使关于x的一元二次方程(m﹣1)x2﹣(2m﹣1)x+m+2=0有实数根的概率是 .
15.(3分)(2022秋 姜堰区期中)如图,飞镖游戏板中每一块小正方形除颜色外都相同.假设飞镖击中每一块小正方形是等可能的(击中小正方形边界或没有击中游戏板,则重投掷一次),任意投掷飞镖1次,则飞镖击中阴影部分的概率是 .
16.(3分)(2022秋 龙岗区校级月考)学校团委在“五四青年节”举行“感动校园十大人物”颁奖活动中,九(4)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动,则甲乙两人恰有一人参加此活动的概率是 .
17.(3分)(2022秋 袁州区校级月考)袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为”,则这个袋中白球大约有 个.
18.(3分)(2022秋 忠县校级月考)一个不透明的口袋中有4个完全相同的小球,球上分别标有数字﹣2,0,1,4.随机摸出一个小球记作m,然后放回,再随机摸出一个小球记作n,则方程mx2﹣2x+n=0是关于x的一元二次方程且此方程无解的概率为 .
三、解答题(共7小题,满分66分)
19.(8分)(2022秋 桐庐县期中)王璐老师为幼儿园小朋友,设计了A,B,C三种款式的围巾和甲,乙两种款式的帽子,供小朋友挑选任一款围巾和一款帽子进行搭配.
(1)用列表或者树状图表示所有搭配可能的结果.
(2)求某个小朋友搭配A款围巾和乙款帽子的概率.
20.(8分)(2022秋 鲤城区校级期中)电子政务、数字经济、智慧社会一场数字革命正在神州大地激荡.某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成统计图表(不完整):请观察下面的图表,解答下列问题:
组别 成绩 人数
A 60≤x<70 10
B 70≤x<80 m
C 80≤x<90 16
D 90≤x<100 4
(1)统计表中m= ;统计图中n= ,D组圆心角的度数是 .
(2)D组的4名学生中,有2名男生和2名女生从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求至少1名女生被抽取参加5G体验活动的概率.
21.(8分)(2022秋 法库县期中)不透明布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出一个球.
(1)第二次摸出白球的概率是多少?(直接写出结论)
(2)请用表格或树状图求出两次都摸出白球的概率.
22.(8分)(2022秋 西湖区校级期中)有四张背面完全相同的纸牌A,B,C,D,其中正面分别写着不同的度数,小华将这四张纸牌背面朝上洗匀后先随机抽出一张(不放回),再随机抽出一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A,B,C,D表示);
(2)求摸出两张纸牌牌面上所写角度恰是互补的概率.
23.(8分)(2022秋 淳安县期中)一个不透明的袋中装有18个红球和若干个白球,它们除颜色外其他均相同.已知将袋中球摇匀后,从中任意摸出一个球是红球的概率是.
(1)求袋中总共有多少个球?
(2)从袋中取走25个球(其中15个红球,10个白球)并将袋中球摇匀后,从剩余的球中任意摸出两个球,求摸出的球是一红一白的概率.
24.(13分)(2022秋 西湖区校级期中)初三年级“黄金分割项目活动”展示,为了解全体初三年级同学的活动成绩,抽取了部分参加活动的同学的成绩进行统计后,分为“优秀”,“良好”,“一般”,“较差”四个等级,并根据成绩绘制成如图两幅不完整的统计图,请结合统计图中的信息,回答下列问题:
(1)扇形统计图中“优秀”所对应扇形的圆心角为 度,并将条形统计图补充完整.
(2)如果学校初三年级共有340名学生,则参加“黄金分割项目活动”比赛成绩良好的学生有 人.
(3)此次活动中有四名同学获得满分,分别是甲,乙,丙,丁,现从这四名同学中挑选两名同学参加校外举行的“黄金分割项目活动”展示,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
25.(13分)(2022秋 锦江区校级期中)成都某中学为了解九年级学生的体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了 名学生,并补全条形图.
(2)“C等级”在扇形图中的圆心角度数为 .
(3)若该中学九年级共有700名学生,请你估计该中学九年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,作为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.
参考答案
一、选择题(共12小题,满分36分,每小题3分)
1.B; 2.A; 3.D; 4.C; 5.B; 6.C; 7.B; 8.C; 9.C; 10.C; 11.D; 12.C;
二、填空题(共6小题,满分18分,每小题3分)
13.
14.
15.
16.
17.3
18.;
三、解答题(共7小题,满分66分)
19.解:(1)画树状图如下:
所有搭配可能的结果有6种;
(2)由(1)可知,所有搭配等可能的结果有6种,其中某个小朋友搭配A款围巾和乙款帽子的结果有1种,
∴某个小朋友搭配A款围巾和乙款帽子的概率为.
20.解:(1)该校八年级参加竞赛的学生人数为:10÷20%=50(人),
∴m=50﹣10﹣16﹣4=20,
n%=16÷50×100%=32%,
∴n=32,
D组的圆心角为:360°28.8°,
故答案为:20,32,28.8°;
(2)画树状图如下:
共有12种等可能的结果,其中至少1名女生被抽取参加5G体验活动的结果有10种,
∴至少1名女生被抽取参加5G体验活动的概率为.
21.解:(1)第二次摸出白球的概率是;
(2)画树状图如下:
共有9种等可能的结果,其中两次都摸出白球的有4种结果,
∴两次都摸出白球的概率为.
22.解:(1)画树状图如下:
两次摸牌所有可能出现的结果共有12种;
(2)由(1)可知,共有12种等可能的结果,其中摸出两张纸牌牌面上所写角度恰是互补的结果有2种,即BD、DB,
∴摸出两张纸牌牌面上所写角度恰是互补的概率为.
23.解:(1)设袋中共有x个球,
∵袋中装有18个红球,从中任意摸出一个球是红球的概率是,
∴,
解得:x=30,
经检验,x=30是原方程的解,
答:袋中总共有30个球.
(2)袋子中白球的个数为:30﹣18=12(个),
取走取走25个球(其中15个红球,10个白球),
则袋子中球的总个数为30﹣25=5(个),红球的个数为:18﹣15=3(个),白球的个数为:12﹣10=2(个),
画树状图如下:
共有20种等可能的结果,其中摸出的球是一红一白的结果有12种,
∴摸出的球是一红一白的概率为.
24.解:(1)抽取的学生人数为:18÷15%=120(人),
∴扇形统计图中“优秀”所对应扇形的圆心角为:360°72°,
∴“良好”等级的人数为120×40%=48(人),
故答案为:72,
把条形统计图补充完整如下:
(2)320×40%=128(人),
∴参加“黄金分割项目活动”比赛成绩良好的学生有128人;
故答案为:128;
(3)画树状图如下:
共有12种等可能的结果,其中选中的两名同学恰好是甲、丁的结果有2种,
∴选中的两名同学恰好是甲、丁的概率.
25.解:(1)10÷20%=50,
所以本次抽样调查共抽取了50名学生;
(2)测试结果为C等级的学生数为50﹣10﹣20﹣4=16(人);
360°115.2°,
(3)70056(名),
所以估计该中学八年级学生中体能测试结果为D等级的学生有56名;
(4)用列表法表示所有可能出现的结果如下:
共有12种等可能的结果数,其中抽取的两人恰好都是男生的结果数为2,
所以抽取的两人恰好都是男生的概率.
10
同课章节目录
