5.2.2平行线的判定课件
文档属性
| 名称 | 5.2.2平行线的判定课件 |  | |
| 格式 | zip | ||
| 文件大小 | 678.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-27 06:28:14 | ||
图片预览


文档简介
课件25张PPT。 5.2.2平行线的判定复习 看图填空(1)若ED,BF被AB所截,
则∠1与_____是同位角。∠2(2)若ED,BC被AF所截,
则∠3与_____是内错角。∠4(3)∠1与∠3是AB和AF被 __ 所截构成的____角。DE内错(4)∠2与∠4是___和__被
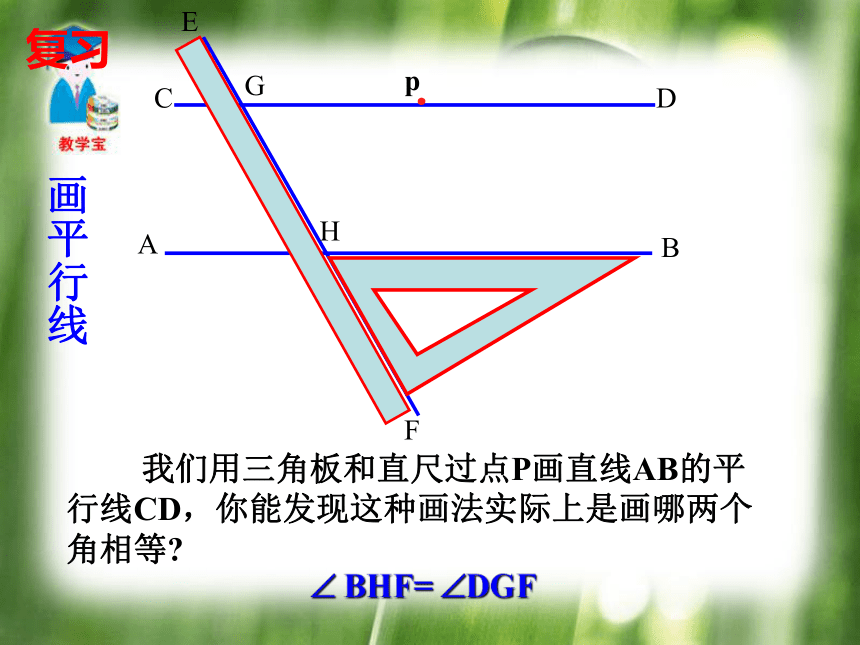
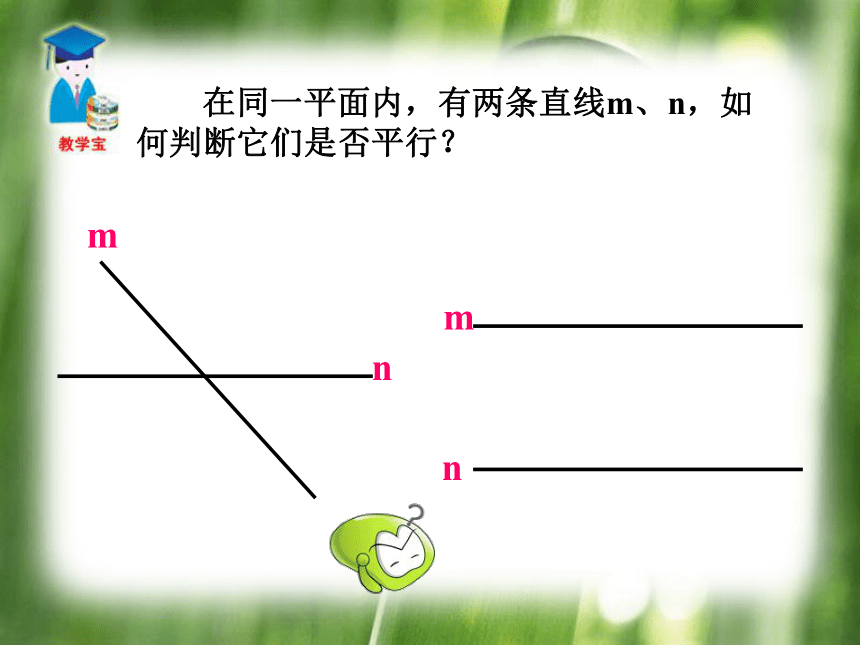
BC所截构成的_____角。ABAF同位? BHF= ?DGF 我们用三角板和直尺过点P画直线AB的平行线CD,你能发现这种画法实际上是画哪两个角相等?HG复习 画平行线 在同一平面内,有两条直线m、n,如何判断它们是否平行?mnmn 在同一平面内,有两条直线a、b如何判断
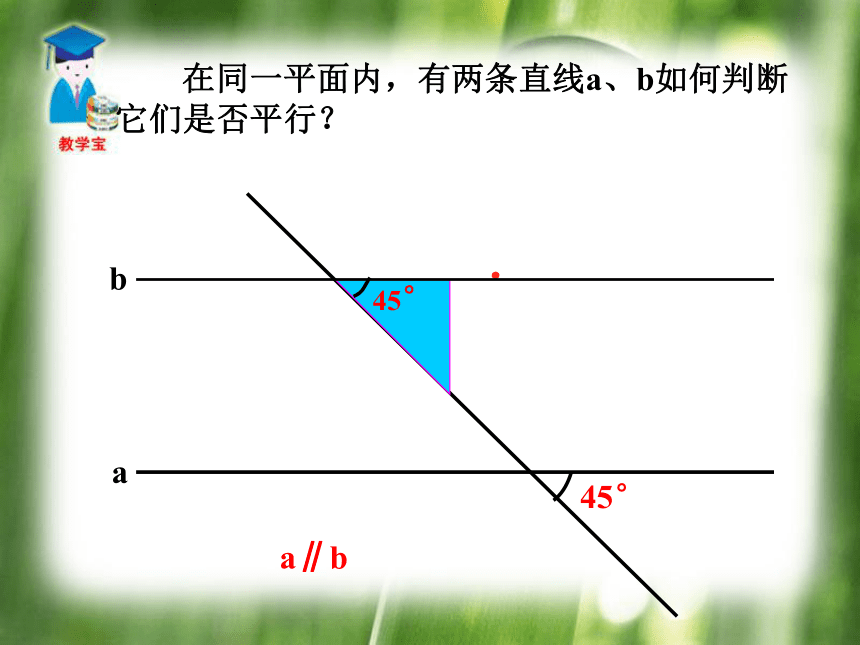
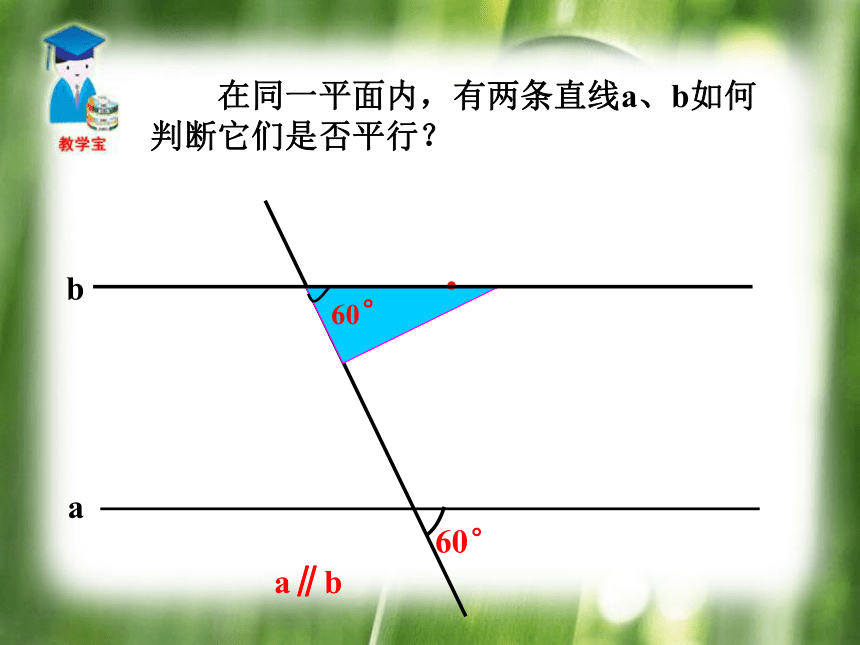
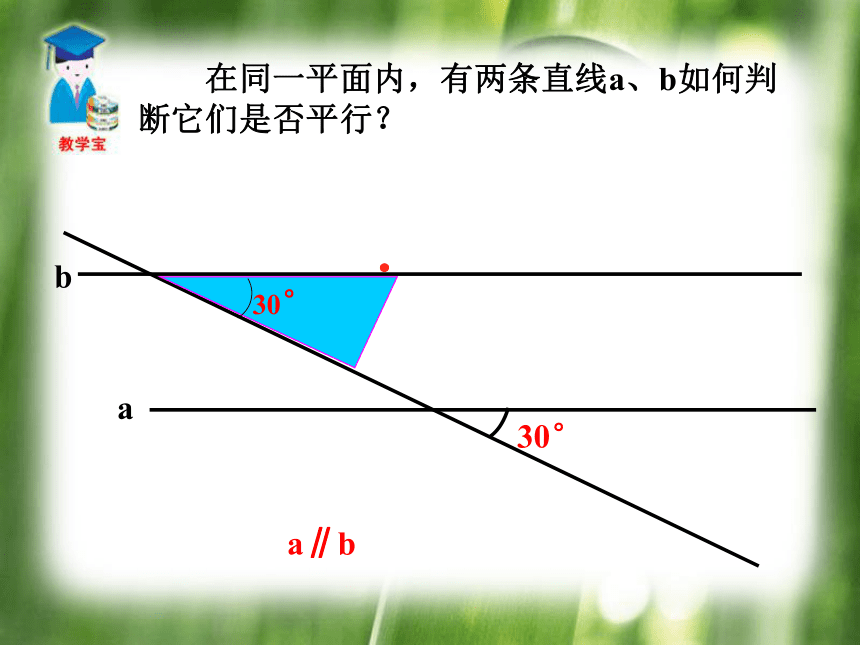
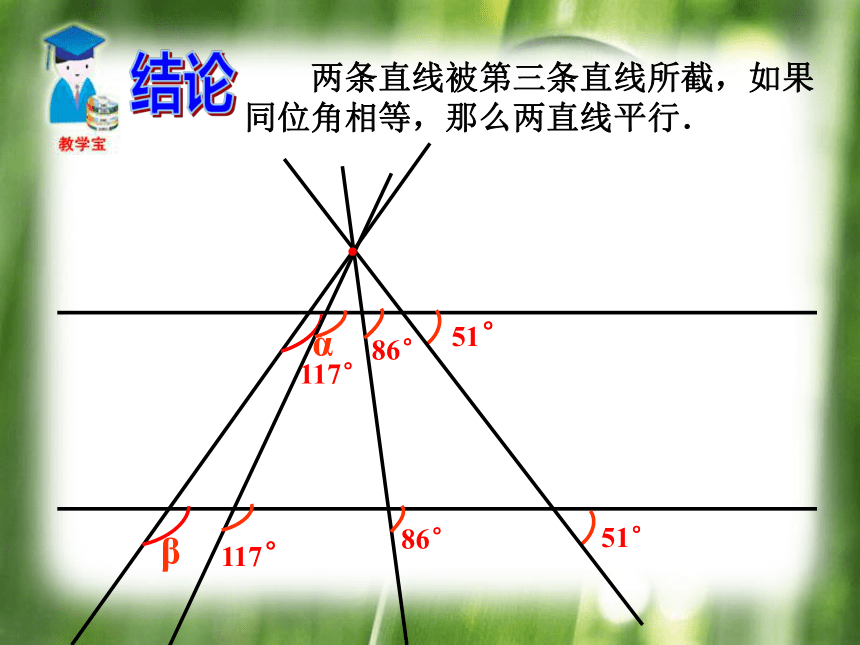
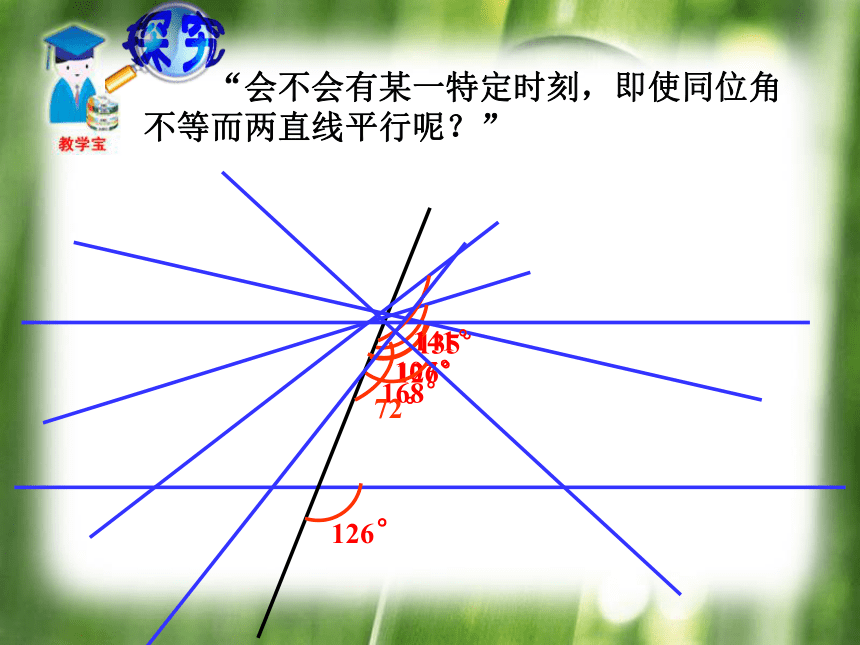
它们是否平行?.45°a∥b 在同一平面内,有两条直线a、b如何判断它们是否平行?●60°a∥b 在同一平面内,有两条直线a、b如何判断它们是否平行?.30°a∥b ● 两条直线被第三条直线所截,如果同位角相等,那么两直线平行.结论 “会不会有某一特定时刻,即使同位角不等而两直线平行呢?” 两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行.简单说成:同位角相等、两直线平行知识要点 平行线的判定方法1:同位角相等两直线平行.即:
因为? DHF= ? BGF,
所以AB ∥CD.EF∥GH∠2 =∠5EF∥GH∠3 =∠4如果 , 能判定哪两条直线平行? ∠1 =∠2AB∥CD如图,哪两个角相等能判定直线AB∥CD?∠3=∠4火眼金睛,找出图中的平行线如果∠ADE=∠ABC,则__∥ __如果∠ACD=∠F, 则__∥ __如果∠DEC=∠BCF,则__∥ __DE BCCD BFDE BC 能否利用内错角和同旁内角来判定两直线平行呢?解: 因为?2=?3(已知)
且?1=?2(对顶角相等)
所以?1= ?3
所以m//n(同位角相等,两直线平行). 如果?2= ?3,m//n?写出你的推导过程. 两条直线被第三条直线所截,如果内错角相等,那么两条直线平行.
简单说成:内错角相等,两直线平行.知识要点 平行线的判定方法2: 如果?1+?2=180° 能判定m//n吗?写出你的推导过程.解: 因为?1+?2=180°
?3+?2=180°
所以?1=?3
所以 m//n(同位角相等,两直线平行) . 两条直线被第三条直线所截,如果同旁内角相等,那么两条直线平行.
简单说成:同旁内角互补,两直线平行.知识要点 平行线的判定方法3:已知条件:直线b与直线c都垂直于直线a.
要说明的结论:直线b与直线c平行吗?例1 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?答:直线b与直线c平行.理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).12你还能用其他方法说明理由吗?例1 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).例2 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么? 例3:已知:如图,∠1=∠4,∠2=∠3,求证: l1∥l2. 解:因为∠1=∠4,
∠3=∠4(对顶角相等),
所以∠1=∠3,
所以 l1∥l3(同位角相等,两直线平行)
因为∠2=∠3(内错角相等,两直线平行),
所以l2∥l3,
所以l1∥l2. 图形条件结论理由同位角内错角同旁内角a//ba//ba//b同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
两直线平行平行线的判定课堂小结∠1=∠2∠2=∠3∠2+∠4=180°1.如果∠A=∠3,那么 ∥ ,
( )
2.如果∠2=∠E,那么 ∥ ,
( )
3.如果∠A+∠ABE=1800,那么 ∥ ,
( )
4.如果∠2= ,那么DA∥EB
( )
5.如果∠DBC+ =1800,那么DB∥EC
( )ABCDE123AD BE同位角相等,两直线平行.BD CE内错角相等,两直线平行.AD BE同旁内角互补,两直线平行.∠D内错角相等,两直线平行.∠C同旁内角互补,两直线平行.反馈评价 游戏接龙① ∵ ∠2 =___(已知)
∴ ___∥___② ∵ ∠3 = ∠5(已知)
∴ ___∥___③∵ ∠4 +___=180o(已知)
∴ ___∥___∠6ABCDABCD∠5ABCD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行反馈评价 游戏接龙
它们是否平行?.45°a∥b 在同一平面内,有两条直线a、b如何判断它们是否平行?●60°a∥b 在同一平面内,有两条直线a、b如何判断它们是否平行?.30°a∥b ● 两条直线被第三条直线所截,如果同位角相等,那么两直线平行.结论 “会不会有某一特定时刻,即使同位角不等而两直线平行呢?” 两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行.简单说成:同位角相等、两直线平行知识要点 平行线的判定方法1:同位角相等两直线平行.即:
因为? DHF= ? BGF,
所以AB ∥CD.EF∥GH∠2 =∠5EF∥GH∠3 =∠4如果 , 能判定哪两条直线平行? ∠1 =∠2AB∥CD如图,哪两个角相等能判定直线AB∥CD?∠3=∠4火眼金睛,找出图中的平行线如果∠ADE=∠ABC,则__∥ __如果∠ACD=∠F, 则__∥ __如果∠DEC=∠BCF,则__∥ __DE BCCD BFDE BC 能否利用内错角和同旁内角来判定两直线平行呢?解: 因为?2=?3(已知)
且?1=?2(对顶角相等)
所以?1= ?3
所以m//n(同位角相等,两直线平行). 如果?2= ?3,m//n?写出你的推导过程. 两条直线被第三条直线所截,如果内错角相等,那么两条直线平行.
简单说成:内错角相等,两直线平行.知识要点 平行线的判定方法2: 如果?1+?2=180° 能判定m//n吗?写出你的推导过程.解: 因为?1+?2=180°
?3+?2=180°
所以?1=?3
所以 m//n(同位角相等,两直线平行) . 两条直线被第三条直线所截,如果同旁内角相等,那么两条直线平行.
简单说成:同旁内角互补,两直线平行.知识要点 平行线的判定方法3:已知条件:直线b与直线c都垂直于直线a.
要说明的结论:直线b与直线c平行吗?例1 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?答:直线b与直线c平行.理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).12你还能用其他方法说明理由吗?例1 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).例2 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么? 例3:已知:如图,∠1=∠4,∠2=∠3,求证: l1∥l2. 解:因为∠1=∠4,
∠3=∠4(对顶角相等),
所以∠1=∠3,
所以 l1∥l3(同位角相等,两直线平行)
因为∠2=∠3(内错角相等,两直线平行),
所以l2∥l3,
所以l1∥l2. 图形条件结论理由同位角内错角同旁内角a//ba//ba//b同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
两直线平行平行线的判定课堂小结∠1=∠2∠2=∠3∠2+∠4=180°1.如果∠A=∠3,那么 ∥ ,
( )
2.如果∠2=∠E,那么 ∥ ,
( )
3.如果∠A+∠ABE=1800,那么 ∥ ,
( )
4.如果∠2= ,那么DA∥EB
( )
5.如果∠DBC+ =1800,那么DB∥EC
( )ABCDE123AD BE同位角相等,两直线平行.BD CE内错角相等,两直线平行.AD BE同旁内角互补,两直线平行.∠D内错角相等,两直线平行.∠C同旁内角互补,两直线平行.反馈评价 游戏接龙① ∵ ∠2 =___(已知)
∴ ___∥___② ∵ ∠3 = ∠5(已知)
∴ ___∥___③∵ ∠4 +___=180o(已知)
∴ ___∥___∠6ABCDABCD∠5ABCD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行反馈评价 游戏接龙
