函数复习
图片预览



文档简介
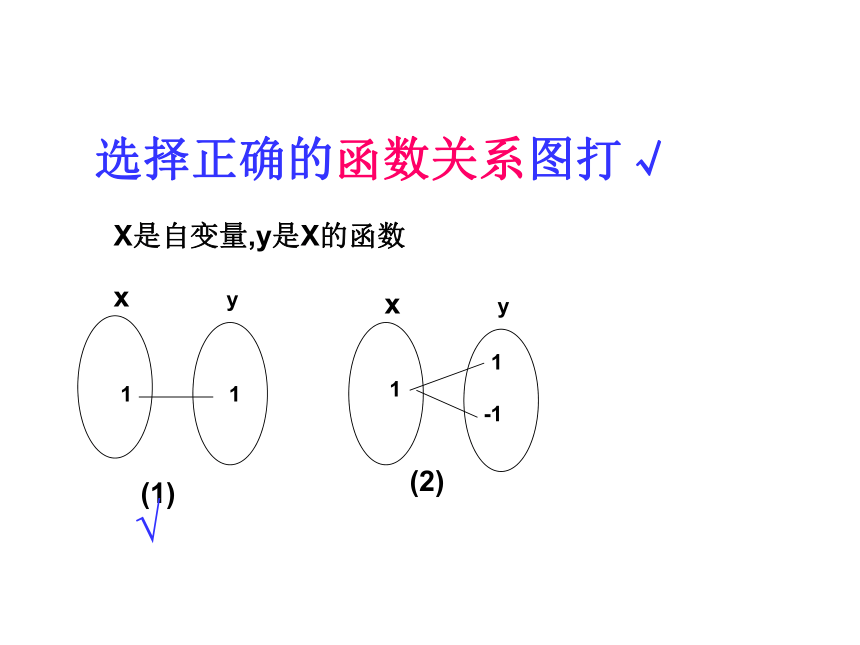
课件22张PPT。函数中的数形结合思想数海拾贝数与形,本是相倚依,焉能分作两边飞.数缺形是少直觉,形少数时难入微.形数结合百般好,隔裂分家万事非.切莫忘,几何代数统一体,永远联系, 莫分离.华罗庚1、函数的定义 如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数 。函数关系是一种特殊的对应关系选择正确的函数关系图打√11xy11-1X是自变量,y是X的函数(1)(2)√(1) 下列关系式中,y是x的函数吗?
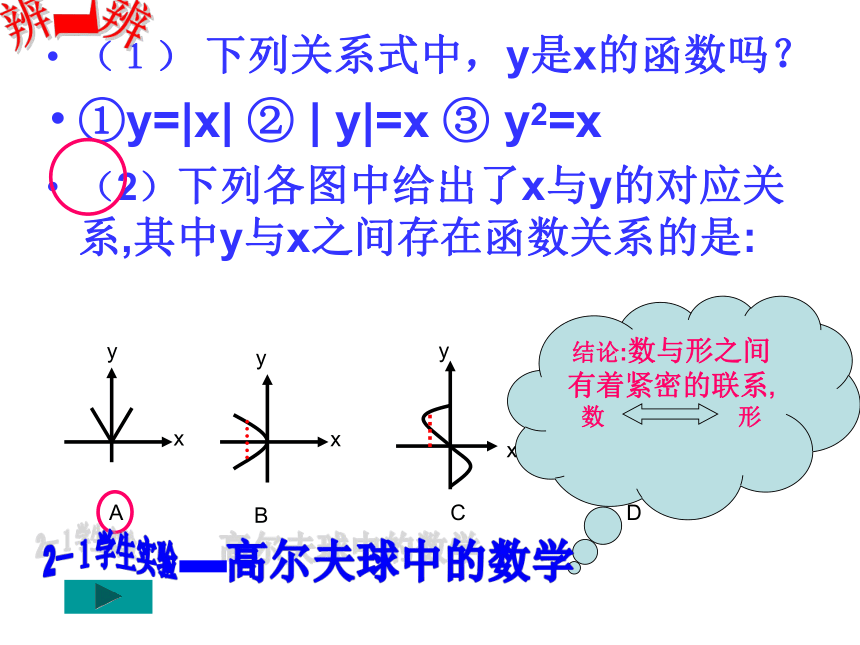
①y=|x| ② | y|=x ③ y2=x
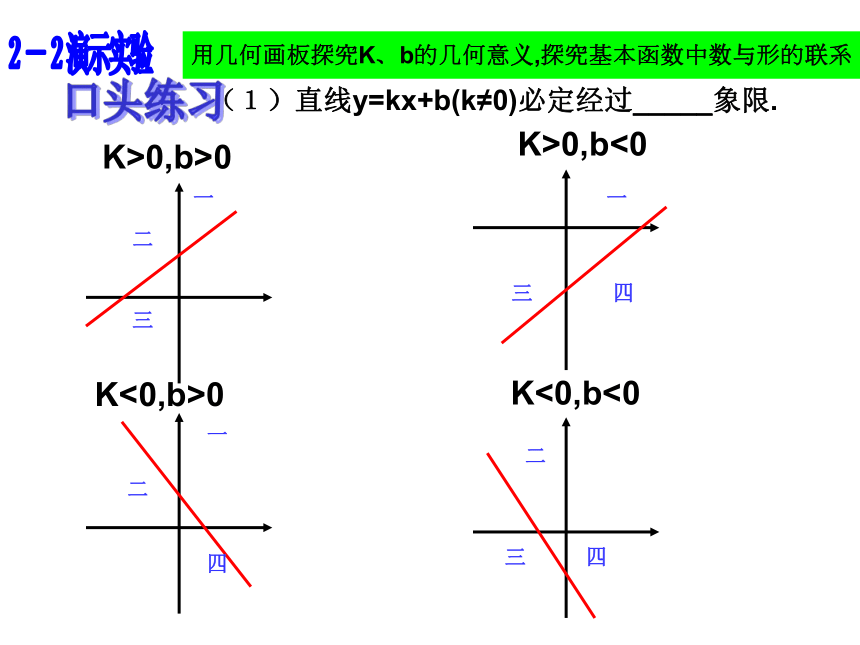
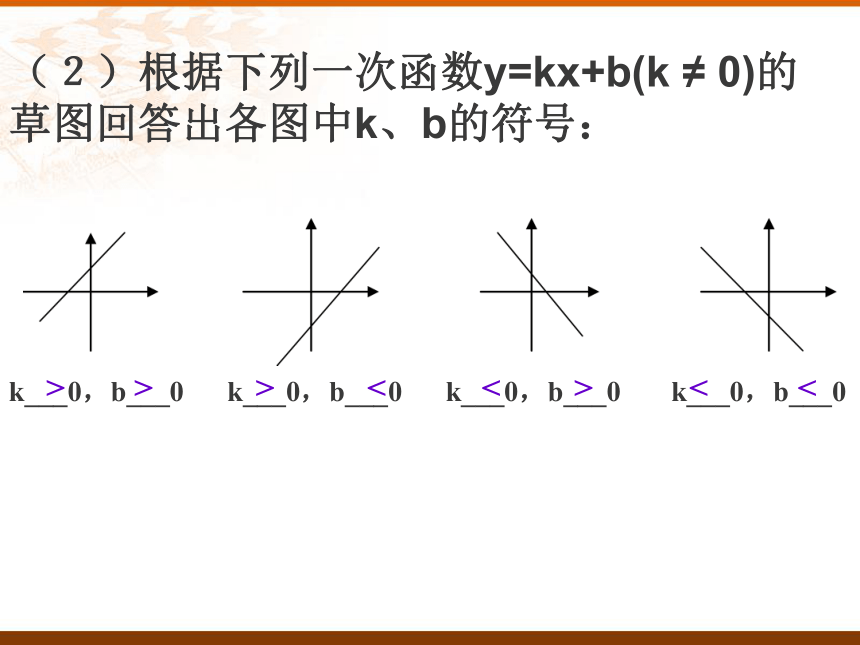
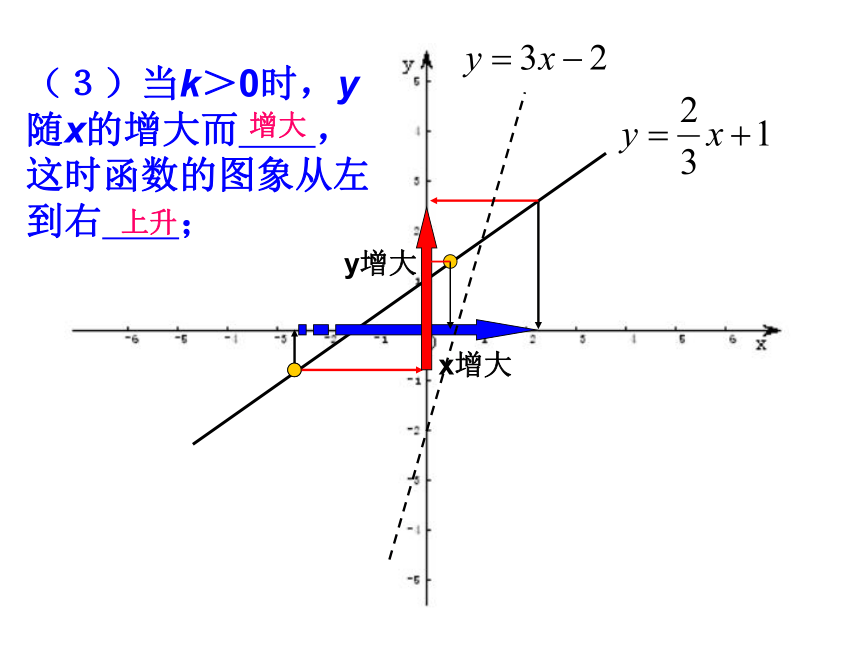
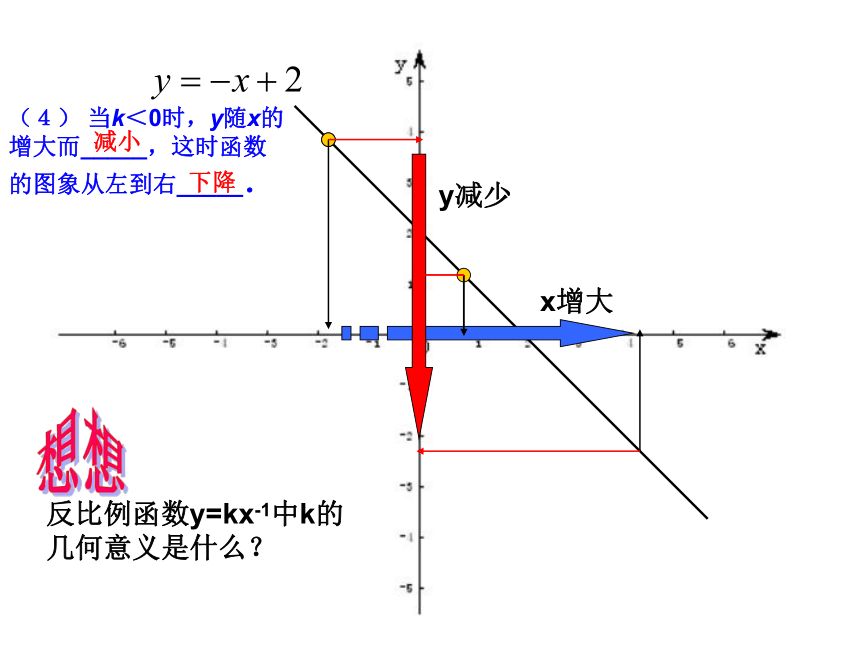
(2)下列各图中给出了x与y的对应关系,其中y与x之间存在函数关系的是:ABCDyxyyyxxx辨一辨K>0,b>0K>0,b<0K<0,b>0K<0,b<0(1)直线y=kx+b(k≠0)必定经过_____象限.2-2演示实验用几何画板探究K、b的几何意义,探究基本函数中数与形的联系口头练习k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0<<><<>>>(2)根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:x增大y增大(3)当k>0时,y随x的增大而 ,这时函数的图象从左到右 ;增大上升x增大y减少(4) 当k<0时,y随x的
增大而_____,这时函数
的图象从左到右_____. 减小下降Oy=kx-1(k≠0)2-3、反比例函数S矩形PBOA=|K|S三角形POA=s□APA’P”=2|K|K的几何意义1)、如图1是三个反比例函数 在轴上方的图象,由此观察得到的大小关系为( )o如下图2,正比例函数y=x与反比例函数y= 1/x 的图象相交于A、C两点,AB⊥X轴,垂足为B,CD⊥X,轴垂足为D,
则四边形ABCD的面积为( )
A、1 B、3/2
C、2 D、5/2 图1图22)巩固E 笛卡儿(Descartes,Rene),1596年3月31日生于拉埃那,今称拉埃耶一笛卡儿(图尔附近)1650年2月11日卒于瑞典斯德哥尔摩。法国哲学家,数学家,物理学家,解析几何学奠基人之一。他认为数学是其他一切科学的理论和模型,提出了数学为基础,以演绎为核心的方法论,对后世的哲学。数学和自然科学发展起到了巨大的作用。
我们现在所用的直角坐标系,通常叫做笛卡儿直角坐标系。是从笛卡儿引进了直角坐标系以后,人们才得以用代数的方法研究几何问题,才建立并完善了解析几何学,才建立了微积分。数学名家笛卡尔①直线y=5x-10过点( ,0)、(0, )
②直线y=-x+3与x轴的交点为 ,与y轴的交点为 .
变式:直线y+2x=1与x轴的交点为 ,与y轴的交点为 .
③点P(-4,-3)到x轴的距离是 ,到轴的距离是 ,到原点的距离是________.
④已知:A(2,-5)、B(5,-1),则线段AB的长是_____.
⑤点A(2,-5)和点B(4,-3) 的中点C的坐标是(__,___)2-10(0.5,0)(0,1)(3,0)(0,3)34553-4抢答知识点:
直线y =kx+b交y轴于点(0,k),交x轴于(- ,0)
简单应用 1、已知直线y=kx-k与双曲线y= (k≠0),则它们在同一坐标系中的图象大致是( )C综合运用2、点P是一个反比例函数与正比例函数y=2x的图象的交点,PQ垂直于x轴,垂足Q的坐标为(2,0).
(1) 求这个反比例函数的解析式.
(2) 如果点M(-4,y)在这个反比例函数的图象上,求点M
的坐标及△MPQ的面积.
(3)在x正半轴上是否存在一点B,使△OPB是等腰三角形?若存在,请求出所有符合条件的点B的坐标;若不存在,请说明理由.
(2,4)2, 48(-4,-2)解:(1)解:(2)、(3)④求直线PM与X轴的交点A,并求出△MPQ的面积AyxB1X-24X设OB1=X⑤求B1yxB1B2
⑥求B224yxB1B2B3⑦求B3解:(1)设P点坐标(2,y),反比例函数为y= (k≠0) ∵直线y=2x过P(2,y) y=2x2=4, ∴ P(2,4) ∵P(2,4)在y= 上,
∴K=8,
∴ y=
(1) 求这个反比例函数的解析式.返规范书写解题过程(2) 如果点M(-4,y)在这个反比例函数的图象上,求点M
的坐标及△MPQ的面积.
(3)在x轴上是否存在一点B,使△OPB是等腰三角形?若存在,请求出所有符合条件的点B的坐标;若不存在,请说明理由.
解题反思:
①点在函数图象上,则点的坐标满足函数关系式。②求交点坐标就是解方程组。
求三角形的面积时,①要充分利用”数形结合”的思想,即用”坐标”求线段,用”线段”求”坐标”②通常将轴上的边作为底边,再利用点的坐标求得底边上的高;然后利用面积公式求解,有时需要将图形分割为规则图形.
待定系数法
(3)在x轴上B1、B2、B3均可让△OPB是等腰三角形
∵设OB1=x,那么QB1=x-2,PB1=x,在Rt△QB1P中(x-2)2+42=x2,解之得X=5,∴ B1(5,0)
∵OP=
B2(2 ,0)
∵OP=PB3 ,PQ⊥ OB3
∴ OB3=2QO=2×2=4
∴B3(4,0)
AB1B2B3
小 结作业自选两道坐标系中求面积的题目.数与形,本是相倚依,焉能分作两边飞.数缺形是少直觉,形少数时难入微.形数结合百般好,隔裂分家万事非.切莫忘,几何代数统一体,永远联系, 莫分离.
①y=|x| ② | y|=x ③ y2=x
(2)下列各图中给出了x与y的对应关系,其中y与x之间存在函数关系的是:ABCDyxyyyxxx辨一辨K>0,b>0K>0,b<0K<0,b>0K<0,b<0(1)直线y=kx+b(k≠0)必定经过_____象限.2-2演示实验用几何画板探究K、b的几何意义,探究基本函数中数与形的联系口头练习k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0<<><<>>>(2)根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:x增大y增大(3)当k>0时,y随x的增大而 ,这时函数的图象从左到右 ;增大上升x增大y减少(4) 当k<0时,y随x的
增大而_____,这时函数
的图象从左到右_____. 减小下降Oy=kx-1(k≠0)2-3、反比例函数S矩形PBOA=|K|S三角形POA=s□APA’P”=2|K|K的几何意义1)、如图1是三个反比例函数 在轴上方的图象,由此观察得到的大小关系为( )o如下图2,正比例函数y=x与反比例函数y= 1/x 的图象相交于A、C两点,AB⊥X轴,垂足为B,CD⊥X,轴垂足为D,
则四边形ABCD的面积为( )
A、1 B、3/2
C、2 D、5/2 图1图22)巩固E 笛卡儿(Descartes,Rene),1596年3月31日生于拉埃那,今称拉埃耶一笛卡儿(图尔附近)1650年2月11日卒于瑞典斯德哥尔摩。法国哲学家,数学家,物理学家,解析几何学奠基人之一。他认为数学是其他一切科学的理论和模型,提出了数学为基础,以演绎为核心的方法论,对后世的哲学。数学和自然科学发展起到了巨大的作用。
我们现在所用的直角坐标系,通常叫做笛卡儿直角坐标系。是从笛卡儿引进了直角坐标系以后,人们才得以用代数的方法研究几何问题,才建立并完善了解析几何学,才建立了微积分。数学名家笛卡尔①直线y=5x-10过点( ,0)、(0, )
②直线y=-x+3与x轴的交点为 ,与y轴的交点为 .
变式:直线y+2x=1与x轴的交点为 ,与y轴的交点为 .
③点P(-4,-3)到x轴的距离是 ,到轴的距离是 ,到原点的距离是________.
④已知:A(2,-5)、B(5,-1),则线段AB的长是_____.
⑤点A(2,-5)和点B(4,-3) 的中点C的坐标是(__,___)2-10(0.5,0)(0,1)(3,0)(0,3)34553-4抢答知识点:
直线y =kx+b交y轴于点(0,k),交x轴于(- ,0)
简单应用 1、已知直线y=kx-k与双曲线y= (k≠0),则它们在同一坐标系中的图象大致是( )C综合运用2、点P是一个反比例函数与正比例函数y=2x的图象的交点,PQ垂直于x轴,垂足Q的坐标为(2,0).
(1) 求这个反比例函数的解析式.
(2) 如果点M(-4,y)在这个反比例函数的图象上,求点M
的坐标及△MPQ的面积.
(3)在x正半轴上是否存在一点B,使△OPB是等腰三角形?若存在,请求出所有符合条件的点B的坐标;若不存在,请说明理由.
(2,4)2, 48(-4,-2)解:(1)解:(2)、(3)④求直线PM与X轴的交点A,并求出△MPQ的面积AyxB1X-24X设OB1=X⑤求B1yxB1B2
⑥求B224yxB1B2B3⑦求B3解:(1)设P点坐标(2,y),反比例函数为y= (k≠0) ∵直线y=2x过P(2,y) y=2x2=4, ∴ P(2,4) ∵P(2,4)在y= 上,
∴K=8,
∴ y=
(1) 求这个反比例函数的解析式.返规范书写解题过程(2) 如果点M(-4,y)在这个反比例函数的图象上,求点M
的坐标及△MPQ的面积.
(3)在x轴上是否存在一点B,使△OPB是等腰三角形?若存在,请求出所有符合条件的点B的坐标;若不存在,请说明理由.
解题反思:
①点在函数图象上,则点的坐标满足函数关系式。②求交点坐标就是解方程组。
求三角形的面积时,①要充分利用”数形结合”的思想,即用”坐标”求线段,用”线段”求”坐标”②通常将轴上的边作为底边,再利用点的坐标求得底边上的高;然后利用面积公式求解,有时需要将图形分割为规则图形.
待定系数法
(3)在x轴上B1、B2、B3均可让△OPB是等腰三角形
∵设OB1=x,那么QB1=x-2,PB1=x,在Rt△QB1P中(x-2)2+42=x2,解之得X=5,∴ B1(5,0)
∵OP=
B2(2 ,0)
∵OP=PB3 ,PQ⊥ OB3
∴ OB3=2QO=2×2=4
∴B3(4,0)
AB1B2B3
小 结作业自选两道坐标系中求面积的题目.数与形,本是相倚依,焉能分作两边飞.数缺形是少直觉,形少数时难入微.形数结合百般好,隔裂分家万事非.切莫忘,几何代数统一体,永远联系, 莫分离.
