13.3角平分线的性质(2)(浙江省嘉兴市郊区)
文档属性
| 名称 | 13.3角平分线的性质(2)(浙江省嘉兴市郊区) |

|
|
| 格式 | rar | ||
| 文件大小 | 175.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-10 00:00:00 | ||
图片预览

文档简介
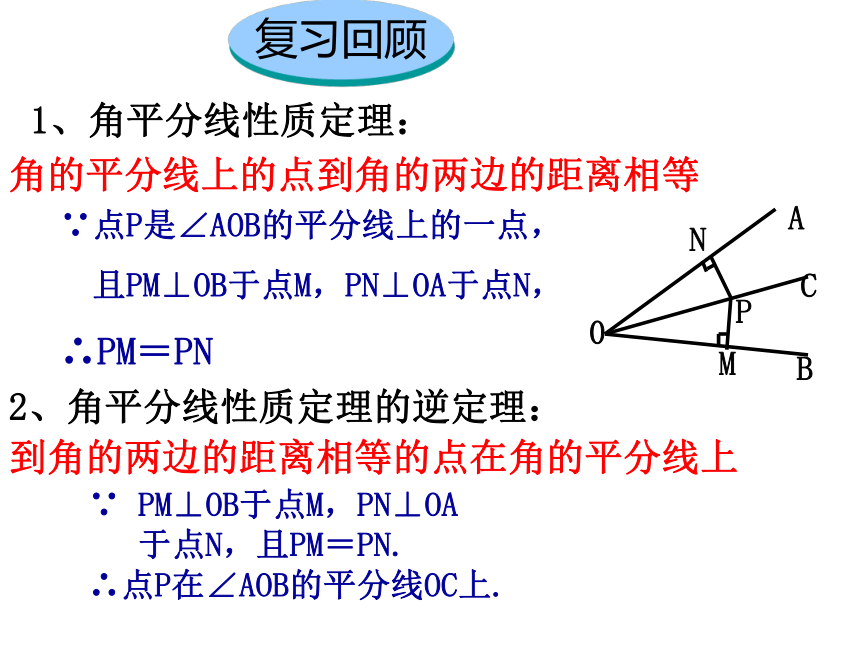
课件13张PPT。13.3 角平分线的性质(2)复习回顾
角的平分线上的点到角的两边的距离相等
2、角平分线性质定理的逆定理:
1、角平分线性质定理:
到角的两边的距离相等的点在角的平分线上∵点P是∠AOB的平分线上的一点,
且PM⊥OB于点M,PN⊥OA于点N,
∴PM=PN
∵ PM⊥OB于点M,PN⊥OA
于点N,且PM=PN.
∴点P在∠AOB的平分线OC上.
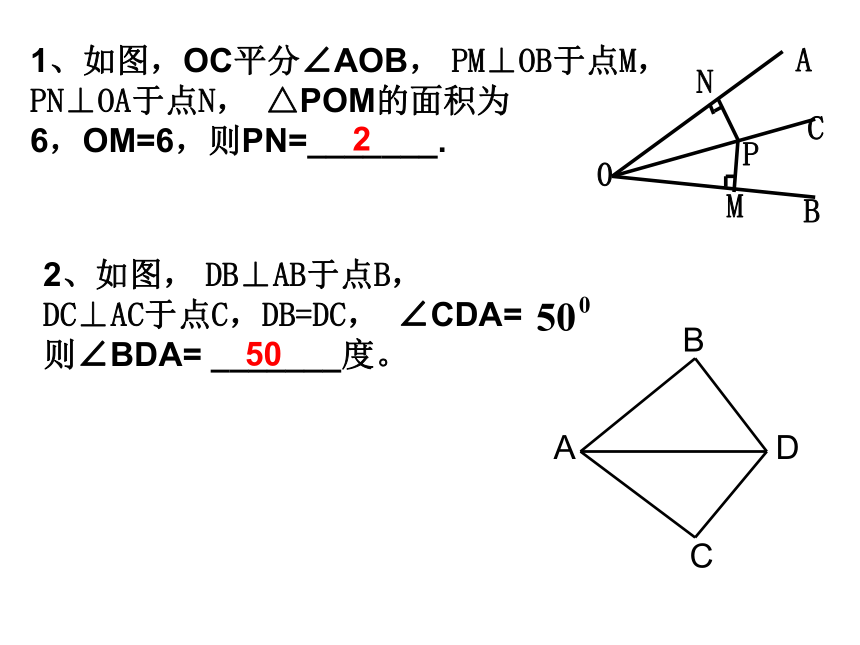
1、如图,OC平分∠AOB, PM⊥OB于点M,
PN⊥OA于点N, △POM的面积为
6,OM=6,则PN=_______.22、如图, DB⊥AB于点B,
DC⊥AC于点C,DB=DC, ∠CDA=
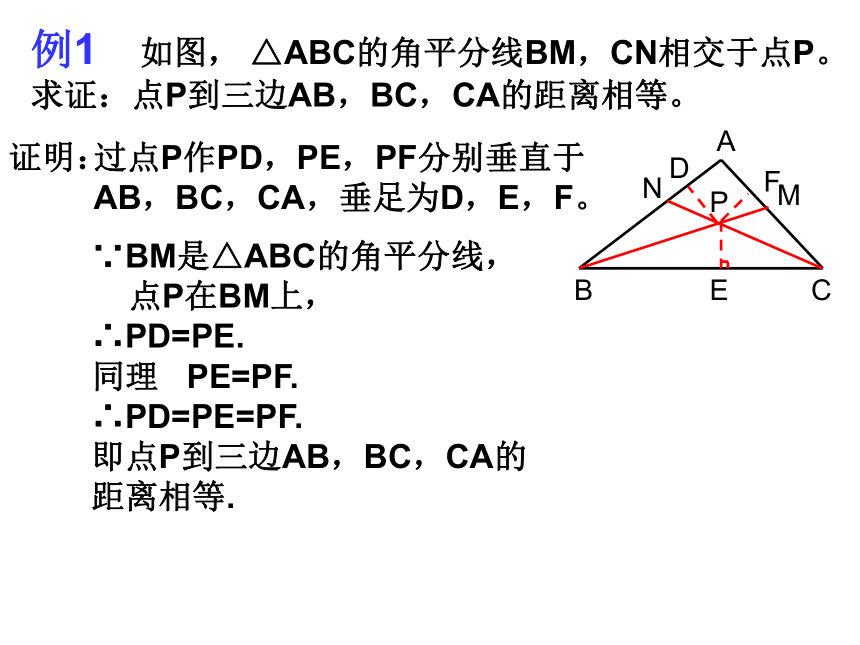
则∠BDA= _______度。50例1 如图, △ABC的角平分线BM,CN相交于点P。
求证:点P到三边AB,BC,CA的距离相等。EFD证明:过点P作PD,PE,PF分别垂直于
AB,BC,CA,垂足为D,E,F。∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.
同理 PE=PF.
∴PD=PE=PF.
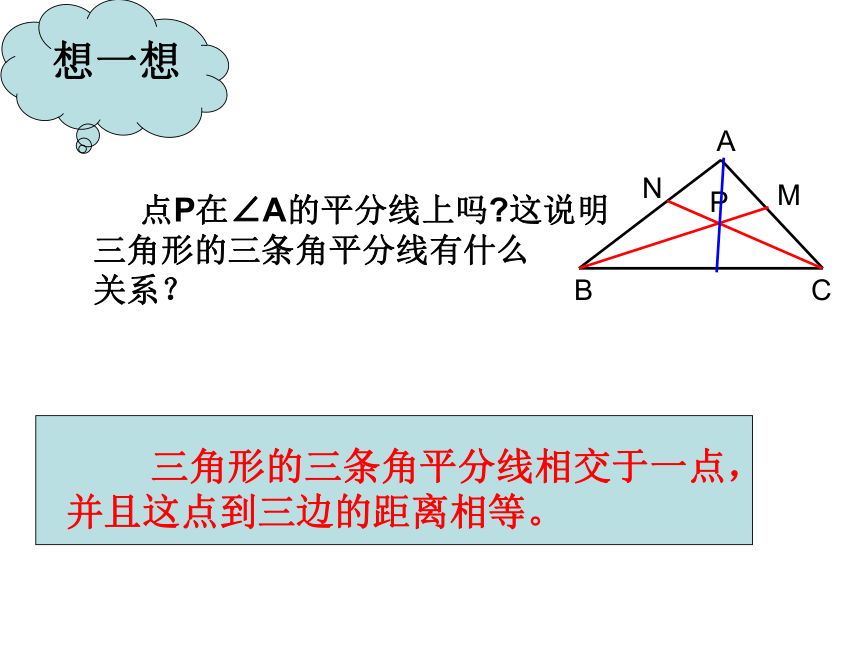
即点P到三边AB,BC,CA的距离相等. 点P在∠A的平分线上吗?这说明
三角形的三条角平分线有什么
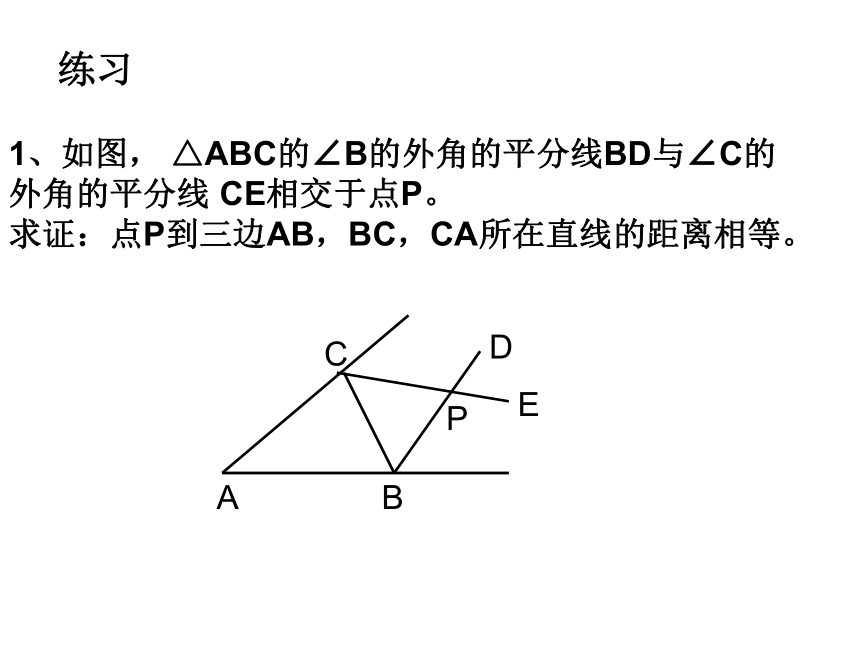
关系?练习1、如图, △ABC的∠B的外角的平分线BD与∠C的
外角的平分线 CE相交于点P。
求证:点P到三边AB,BC,CA所在直线的距离相等。
2、如图所示,直线 表示三条相互交叉的
公路,现要建一个货物中转站,要求它到三条公路的
距离相等,则可供选择的地址有: ( )
A、一处 B、两处 C、三处 D、四处D例2、如图, PB⊥AB于点B,PC⊥AC于点C,
PB=PC, D是AP上一点。
求证:∠BDP=∠CDP。
例3、已知,如图, ∠B=∠C= ,M是BC的中点,
DM平分∠ADC。
求证:AM平分∠DAB。证明:过M作ME⊥AD于EE
二是运用角平分线的判定方法,若没有垂线段,
则需作辅助线添加出来。证明角平分线有两种方法:一是运用定义证明两个角相等(有时需要用等角转换); 已知AB//CD,O是∠BAC、 ∠ACD的平分线的
交点,OE⊥AC于E,且OE=2cm,则两平行线AB、
CD之间的距离是______.4cm变式:4、 △ABC中, ∠ C= , AC=BC,AD是△ABC
的角平分线, DE⊥AB于E,若AB=20cm,则△DBE的
周长等于_________.20cm5、如图, AD是△ABC的角平分线,DE⊥AB,
DF⊥AC,垂足分别是E、F,连接EF,EF与AD
交于G。求证:
(1) ∠DEF=∠DFE。(2)AE=AF(3) AD⊥EF
角的平分线上的点到角的两边的距离相等
2、角平分线性质定理的逆定理:
1、角平分线性质定理:
到角的两边的距离相等的点在角的平分线上∵点P是∠AOB的平分线上的一点,
且PM⊥OB于点M,PN⊥OA于点N,
∴PM=PN
∵ PM⊥OB于点M,PN⊥OA
于点N,且PM=PN.
∴点P在∠AOB的平分线OC上.
1、如图,OC平分∠AOB, PM⊥OB于点M,
PN⊥OA于点N, △POM的面积为
6,OM=6,则PN=_______.22、如图, DB⊥AB于点B,
DC⊥AC于点C,DB=DC, ∠CDA=
则∠BDA= _______度。50例1 如图, △ABC的角平分线BM,CN相交于点P。
求证:点P到三边AB,BC,CA的距离相等。EFD证明:过点P作PD,PE,PF分别垂直于
AB,BC,CA,垂足为D,E,F。∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.
同理 PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等. 点P在∠A的平分线上吗?这说明
三角形的三条角平分线有什么
关系?练习1、如图, △ABC的∠B的外角的平分线BD与∠C的
外角的平分线 CE相交于点P。
求证:点P到三边AB,BC,CA所在直线的距离相等。
2、如图所示,直线 表示三条相互交叉的
公路,现要建一个货物中转站,要求它到三条公路的
距离相等,则可供选择的地址有: ( )
A、一处 B、两处 C、三处 D、四处D例2、如图, PB⊥AB于点B,PC⊥AC于点C,
PB=PC, D是AP上一点。
求证:∠BDP=∠CDP。
例3、已知,如图, ∠B=∠C= ,M是BC的中点,
DM平分∠ADC。
求证:AM平分∠DAB。证明:过M作ME⊥AD于EE
二是运用角平分线的判定方法,若没有垂线段,
则需作辅助线添加出来。证明角平分线有两种方法:一是运用定义证明两个角相等(有时需要用等角转换); 已知AB//CD,O是∠BAC、 ∠ACD的平分线的
交点,OE⊥AC于E,且OE=2cm,则两平行线AB、
CD之间的距离是______.4cm变式:4、 △ABC中, ∠ C= , AC=BC,AD是△ABC
的角平分线, DE⊥AB于E,若AB=20cm,则△DBE的
周长等于_________.20cm5、如图, AD是△ABC的角平分线,DE⊥AB,
DF⊥AC,垂足分别是E、F,连接EF,EF与AD
交于G。求证:
(1) ∠DEF=∠DFE。(2)AE=AF(3) AD⊥EF
