5.3.1平行线的性质课件
图片预览




文档简介
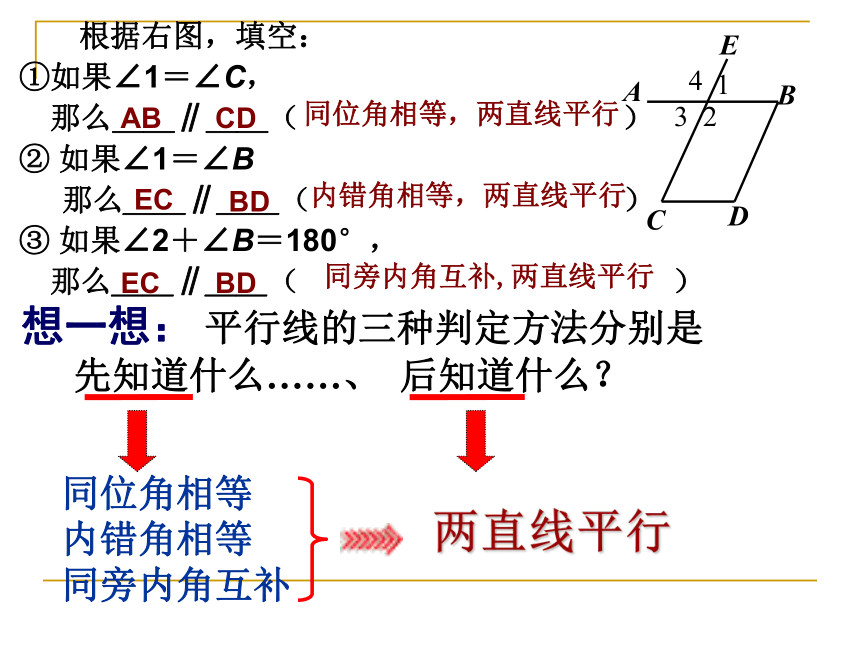
课件26张PPT。5.3.1平行线的性质 根据右图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,
那么__∥__( ) 想一想: 平行线的三种判定方法分别是
先知道什么……、 后知道什么? 同位角相等
内错角相等
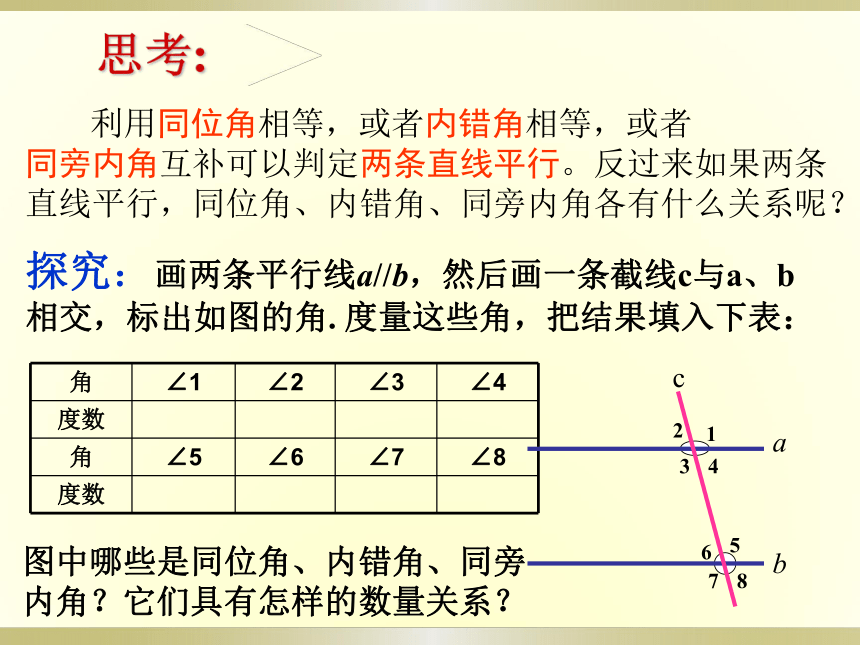
同旁内角互补两直线平行ABCDECBD同位角相等,两直线平行内错角相等,两直线平行ECBD同旁内角互补,两直线平行探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 度量这些角,把结果填入下表: 利用同位角相等,或者内错角相等,或者
同旁内角互补可以判定两条直线平行。反过来如果两条
直线平行,同位角、内错角、同旁内角各有什么关系呢?思考:图中哪些是同位角、内错角、同旁内角?它们具有怎样的数量关系?观察与猜想: 各对同位角、内错角、同旁内角的度数之间有什么关系?说出你的猜想: 猜想:
两条平行线被第三条直线所截,同位角____,
内错角_____,同旁内角_____。 再任意画一条截线d,同样度量并计算各个角
的度数,你的猜想还成立吗?相等相等互补性质1:两条平行线被第三条直线所截,同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.平行线的性质:简单说成:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
思考: 如右图,已知:a// b ,那么
(1)?3与?2有什么关系?为什么?
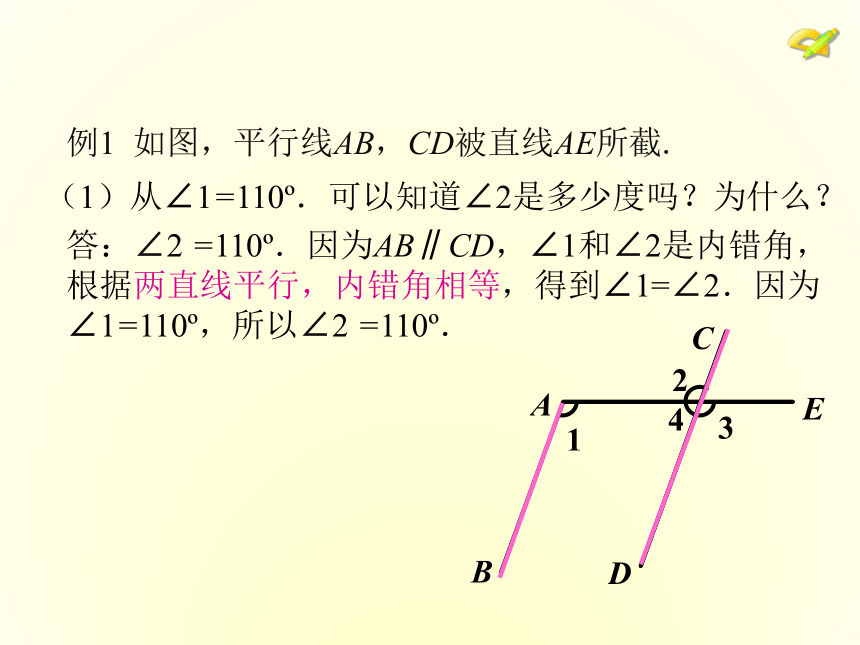
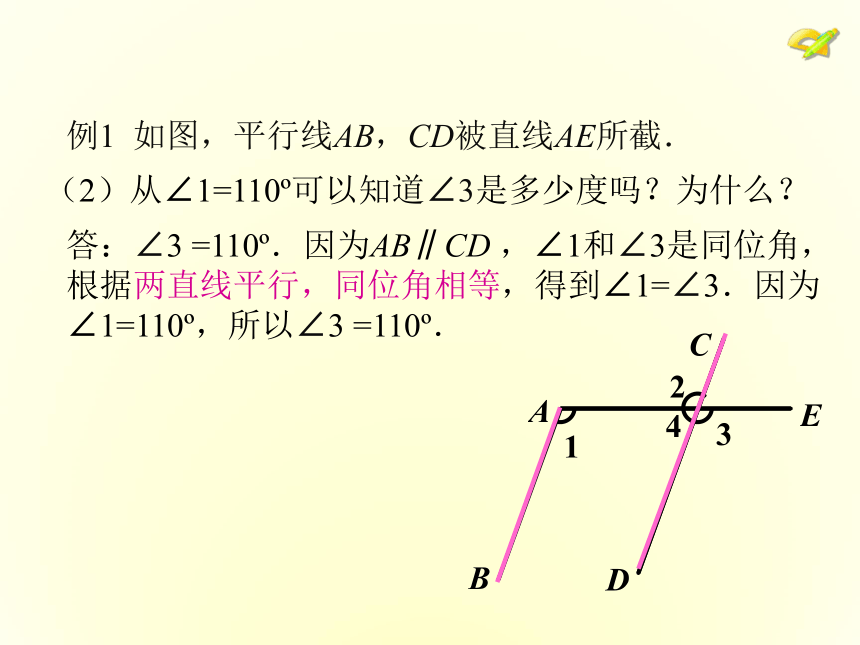
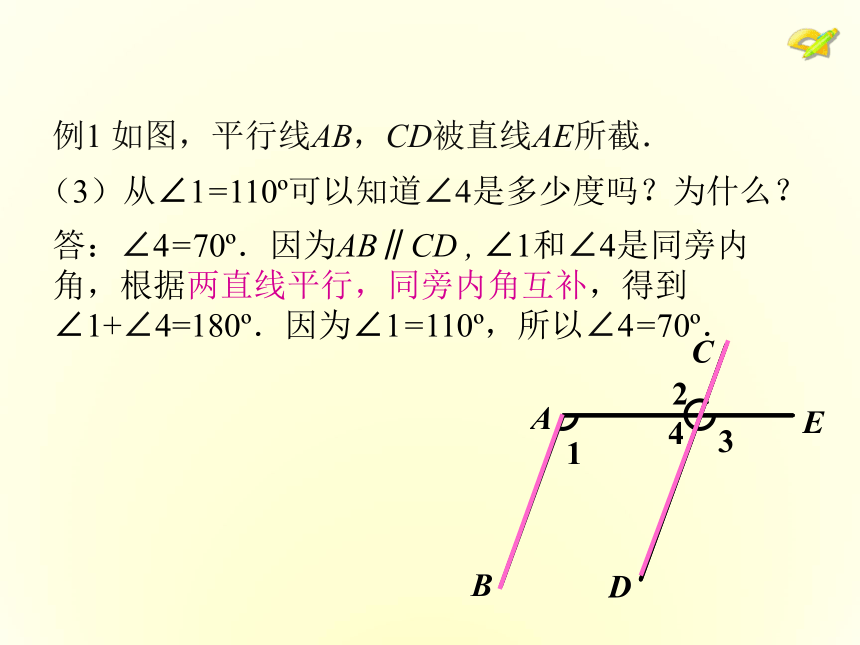
(2) ?2与?4有什么关系?为什么?你能根据性质1,推出性质2、3吗??4(1)从∠1=110o.可以知道∠2是多少度吗?为什么?答:∠2 =110o.因为AB∥CD,∠1和∠2是内错角,根据两直线平行,内错角相等,得到∠1=∠2.因为∠1=110o,所以∠2 =110o.例1 如图,平行线AB,CD被直线AE所截.(2)从∠1=110o可以知道∠3是多少度吗?为什么?例1 如图,平行线AB,CD被直线AE所截.答:∠3 =110o.因为AB∥CD ,∠1和∠3是同位角,根据两直线平行,同位角相等,得到∠1=∠3.因为∠1=110o,所以∠3 =110o.(3)从∠1=110o可以知道∠4是多少度吗?为什么?例1 如图,平行线AB,CD被直线AE所截.答:∠4=70o.因为AB∥CD , ∠1和∠4是同旁内角,根据两直线平行,同旁内角互补,得到∠1+∠4=180o.因为∠1=110o,所以∠4=70o.例2 如图,已知AB∥CD,AE∥CF,∠A= 39°,
∠C是多少度?为什么?方法一
解:∵AB∥CD,
∴ ∠C=∠1.
∵ AE∥CF,
∴ ∠A=∠1.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.1方法二
解:∵AB∥CD,
∴ ∠C=∠2.
∵ AE∥CF,
∴ ∠A=∠2.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.2解:因为梯形上、下两底 AB∥CD ,
根据“两直线平行,同旁内角互补”,
可得∠A+∠D =180o,∠B+∠C =180o.
于是∠D =180o-∠A
=180o-100oo =80o ,
∠C =180o-∠B
=180o-115o =65o .
所以,梯形的另外两个角分别是80o,65o .例3 如图,是一块梯形铁片的残余部分,量得∠A=100o,∠B=115o,梯形的另外两个角分别是多少度?理由如下:
∵ CE∥BF,
∴∠1=∠B.
∵∠1=∠2 ,
∴∠2=∠B.
∵∠2和∠B是内错角,
∴ AB∥CD(内错角相等,两直线平行).例4 已知,如图,∠1=∠2,CE∥BF,
试说明: AB∥CD.练习:已知∠3 =∠4,∠1=47°,求∠2的度数?∴∠ 2= 470
( )解:∵ ∠3 =∠4( )∴a∥b
( )
又∵∠ 1 = 470 ( )c1234abd解: 因为 ∠1=82°, ∠2=98° (已知)
所以∠1+∠2= ( )
又因为 +∠5=180°( )
所以 ∠1=∠5 ( )
所以 a//b ( )
所以 =∠4 ( )
又因为 ∠3=80°(已知)
所以 ( )180°等式性质∠2邻补角的定义同角的补角相等同位角相等,两直线平行∠3两直线平行,内错角相等∠4=80°等量代换随堂练习 1.如图,∠1=82°, ∠2=98°,∠3=80°,求∠4的度数.理由如下:
∵ BE平分∠ABC,
∴
同理
∵ AB∥CD,
∴∠ABC=∠BCD.
∴∠1=∠2.
∵∠1和∠2是内错角,
∴ BE∥CF(内错角相等,两直线平行).练习1 如图,AB∥CD,BE平分∠ABC,CF平分
∠BCD,你能发现BE与CF的位置关系吗?说明理由.解: BE∥CF.理由如下:
∵ ∠AGD =∠ACB ,
∴ GD∥BC.
∵∠1和∠3是内错角,
∴∠1=∠3(两直线平行,内错角相等).
∵∠1=∠2,
∴∠2=∠3.
∵∠2和∠3是同位角,
∴ CD∥EF(同位角相等,两直线平行).3练习2 已知:如图,∠AGD=∠ACB,
∠1=∠2,CD与EF平行吗?为什么?解:CD∥EF.练习3 如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?练习3
已知条件:如图,AB∥CD,∠1=∠2,∠3=∠4.
猜想:∠2和∠3有什么关系,并说明理由;
试说明:PM∥NQ.答:∠2=∠3.
理由如下:
∵ AB∥CD ,
∴ ∠2=∠3(两直线平行,内错角相等).已知条件:如图,AB∥CD,∠1=∠2,∠3=∠4.
试说明:PM∥NQ.理由如下:
∵∠1=∠2 ,∠3=∠4,
又∵∠2=∠3.
∴∠1=∠2 =∠3=∠4.
∵∠1+∠2 +∠5=180o,∠3+∠4 +∠6=180o,
∴∠5=∠6.
∵∠5和∠6是内错角,
∴ PM∥NQ (内错角相等,两直线平行).小结:对比平行线的性质和判定方法,你能说出它们的区别吗? 2.在下图所示的3个图中,a∥b,
分别计算∠1的度数.DCAB1aaabbb11136°120°1.如图1,AB∥CD, ∠1=45°
且∠D=∠C,
求出∠D, ∠C, ∠B的度数.试试看:36°120°巩固练习:
1.如图,直线a∥b, ∠ 1=54o,
那么∠2、∠3、∠4各是多少度?1234答:∠2 = ∠ 1=54o( ),
∠4 = ∠ 1=54o( ),
∠3=180°-∠4
=180°-54°=126°( ) 对顶角相等两直线平行,同位角相等邻补角的定义2.如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°。 (1)DE和BC平行吗?为什么? (2)∠C是多少度?为什么? 答:(1)DE∥BC,
因为∠ADE=60°,∠B=60°,
所以∠ADE= ∠B.
所以DE∥BC ( )同位角相等,两直线平行(2) ∠C =40°.
因为DE∥BC ,
所以∠C = ∠AED.( )
因为∠AED=40°,所以∠C =40°.两直线平行,同位角相等再见
祝同学们学习进步
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,
那么__∥__( ) 想一想: 平行线的三种判定方法分别是
先知道什么……、 后知道什么? 同位角相等
内错角相等
同旁内角互补两直线平行ABCDECBD同位角相等,两直线平行内错角相等,两直线平行ECBD同旁内角互补,两直线平行探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 度量这些角,把结果填入下表: 利用同位角相等,或者内错角相等,或者
同旁内角互补可以判定两条直线平行。反过来如果两条
直线平行,同位角、内错角、同旁内角各有什么关系呢?思考:图中哪些是同位角、内错角、同旁内角?它们具有怎样的数量关系?观察与猜想: 各对同位角、内错角、同旁内角的度数之间有什么关系?说出你的猜想: 猜想:
两条平行线被第三条直线所截,同位角____,
内错角_____,同旁内角_____。 再任意画一条截线d,同样度量并计算各个角
的度数,你的猜想还成立吗?相等相等互补性质1:两条平行线被第三条直线所截,同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.平行线的性质:简单说成:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
思考: 如右图,已知:a// b ,那么
(1)?3与?2有什么关系?为什么?
(2) ?2与?4有什么关系?为什么?你能根据性质1,推出性质2、3吗??4(1)从∠1=110o.可以知道∠2是多少度吗?为什么?答:∠2 =110o.因为AB∥CD,∠1和∠2是内错角,根据两直线平行,内错角相等,得到∠1=∠2.因为∠1=110o,所以∠2 =110o.例1 如图,平行线AB,CD被直线AE所截.(2)从∠1=110o可以知道∠3是多少度吗?为什么?例1 如图,平行线AB,CD被直线AE所截.答:∠3 =110o.因为AB∥CD ,∠1和∠3是同位角,根据两直线平行,同位角相等,得到∠1=∠3.因为∠1=110o,所以∠3 =110o.(3)从∠1=110o可以知道∠4是多少度吗?为什么?例1 如图,平行线AB,CD被直线AE所截.答:∠4=70o.因为AB∥CD , ∠1和∠4是同旁内角,根据两直线平行,同旁内角互补,得到∠1+∠4=180o.因为∠1=110o,所以∠4=70o.例2 如图,已知AB∥CD,AE∥CF,∠A= 39°,
∠C是多少度?为什么?方法一
解:∵AB∥CD,
∴ ∠C=∠1.
∵ AE∥CF,
∴ ∠A=∠1.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.1方法二
解:∵AB∥CD,
∴ ∠C=∠2.
∵ AE∥CF,
∴ ∠A=∠2.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.2解:因为梯形上、下两底 AB∥CD ,
根据“两直线平行,同旁内角互补”,
可得∠A+∠D =180o,∠B+∠C =180o.
于是∠D =180o-∠A
=180o-100oo =80o ,
∠C =180o-∠B
=180o-115o =65o .
所以,梯形的另外两个角分别是80o,65o .例3 如图,是一块梯形铁片的残余部分,量得∠A=100o,∠B=115o,梯形的另外两个角分别是多少度?理由如下:
∵ CE∥BF,
∴∠1=∠B.
∵∠1=∠2 ,
∴∠2=∠B.
∵∠2和∠B是内错角,
∴ AB∥CD(内错角相等,两直线平行).例4 已知,如图,∠1=∠2,CE∥BF,
试说明: AB∥CD.练习:已知∠3 =∠4,∠1=47°,求∠2的度数?∴∠ 2= 470
( )解:∵ ∠3 =∠4( )∴a∥b
( )
又∵∠ 1 = 470 ( )c1234abd解: 因为 ∠1=82°, ∠2=98° (已知)
所以∠1+∠2= ( )
又因为 +∠5=180°( )
所以 ∠1=∠5 ( )
所以 a//b ( )
所以 =∠4 ( )
又因为 ∠3=80°(已知)
所以 ( )180°等式性质∠2邻补角的定义同角的补角相等同位角相等,两直线平行∠3两直线平行,内错角相等∠4=80°等量代换随堂练习 1.如图,∠1=82°, ∠2=98°,∠3=80°,求∠4的度数.理由如下:
∵ BE平分∠ABC,
∴
同理
∵ AB∥CD,
∴∠ABC=∠BCD.
∴∠1=∠2.
∵∠1和∠2是内错角,
∴ BE∥CF(内错角相等,两直线平行).练习1 如图,AB∥CD,BE平分∠ABC,CF平分
∠BCD,你能发现BE与CF的位置关系吗?说明理由.解: BE∥CF.理由如下:
∵ ∠AGD =∠ACB ,
∴ GD∥BC.
∵∠1和∠3是内错角,
∴∠1=∠3(两直线平行,内错角相等).
∵∠1=∠2,
∴∠2=∠3.
∵∠2和∠3是同位角,
∴ CD∥EF(同位角相等,两直线平行).3练习2 已知:如图,∠AGD=∠ACB,
∠1=∠2,CD与EF平行吗?为什么?解:CD∥EF.练习3 如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?练习3
已知条件:如图,AB∥CD,∠1=∠2,∠3=∠4.
猜想:∠2和∠3有什么关系,并说明理由;
试说明:PM∥NQ.答:∠2=∠3.
理由如下:
∵ AB∥CD ,
∴ ∠2=∠3(两直线平行,内错角相等).已知条件:如图,AB∥CD,∠1=∠2,∠3=∠4.
试说明:PM∥NQ.理由如下:
∵∠1=∠2 ,∠3=∠4,
又∵∠2=∠3.
∴∠1=∠2 =∠3=∠4.
∵∠1+∠2 +∠5=180o,∠3+∠4 +∠6=180o,
∴∠5=∠6.
∵∠5和∠6是内错角,
∴ PM∥NQ (内错角相等,两直线平行).小结:对比平行线的性质和判定方法,你能说出它们的区别吗? 2.在下图所示的3个图中,a∥b,
分别计算∠1的度数.DCAB1aaabbb11136°120°1.如图1,AB∥CD, ∠1=45°
且∠D=∠C,
求出∠D, ∠C, ∠B的度数.试试看:36°120°巩固练习:
1.如图,直线a∥b, ∠ 1=54o,
那么∠2、∠3、∠4各是多少度?1234答:∠2 = ∠ 1=54o( ),
∠4 = ∠ 1=54o( ),
∠3=180°-∠4
=180°-54°=126°( ) 对顶角相等两直线平行,同位角相等邻补角的定义2.如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°。 (1)DE和BC平行吗?为什么? (2)∠C是多少度?为什么? 答:(1)DE∥BC,
因为∠ADE=60°,∠B=60°,
所以∠ADE= ∠B.
所以DE∥BC ( )同位角相等,两直线平行(2) ∠C =40°.
因为DE∥BC ,
所以∠C = ∠AED.( )
因为∠AED=40°,所以∠C =40°.两直线平行,同位角相等再见
祝同学们学习进步
