绝对值(1)(浙江省台州市温岭市)
文档属性
| 名称 | 绝对值(1)(浙江省台州市温岭市) |

|
|
| 格式 | rar | ||
| 文件大小 | 61.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-11 00:00:00 | ||
图片预览




文档简介
课件15张PPT。1.2.4 绝对值 例1:两位同学在书店购买书籍后坐出租车回家,
甲车向东行驶了10公里和乙车向西行驶了10公里
(1)请用数轴表示这一过程
(记向东行驶的路程数为正)
情景引入:OBA010-1010105-5 例1:两位同学在书店购买书籍后坐出租车回家,
甲车向东行驶了10公里和乙车向西行驶了10公里
(1)请用数轴表示这一过程
(记向东行驶的路程数为正)
(2)若已知出租车前3公里收费10元,后面每
公里收费2元,还要加收每车次一元的燃油费,
问小明 和小华分别要付多少车费?
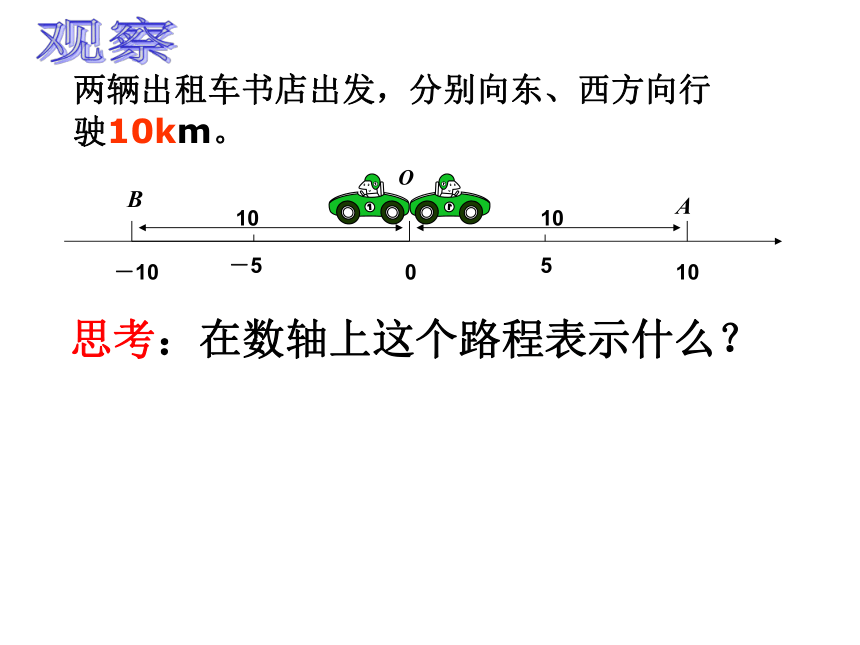
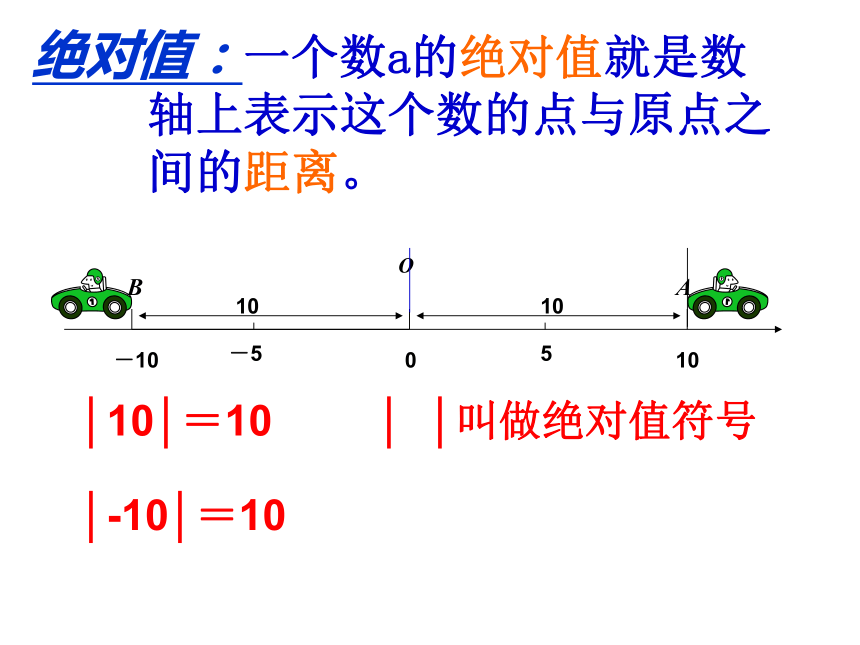
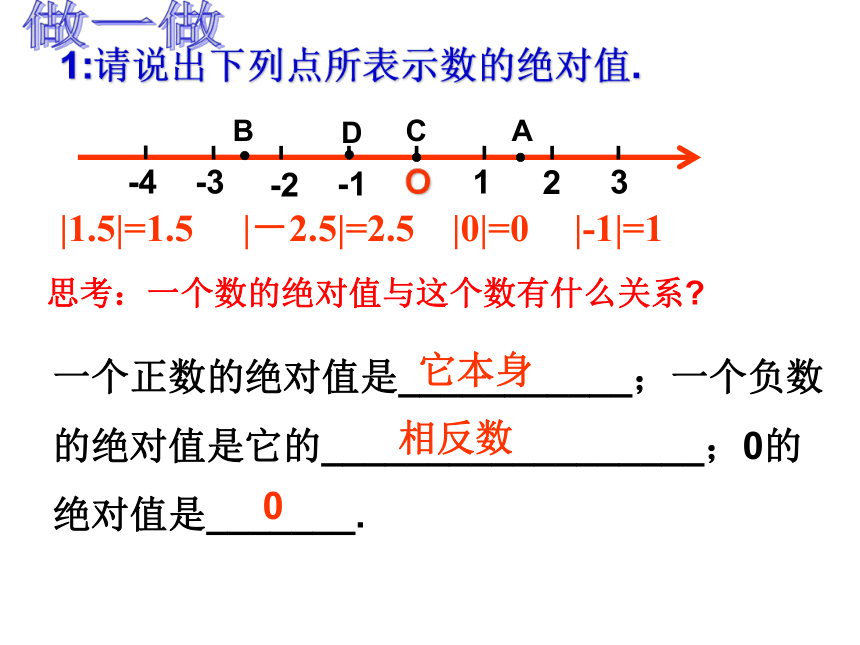
(3)所付的出租车费与行驶的方向有没有关系?(4)所付的出租车费与什么有关系?观察两辆出租车书店出发,分别向东、西方向行驶10km。OBA010-1010105-5思考:在数轴上这个路程表示什么?绝对值 在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值(absolute value).距离OBA010-1010105-5 一个数a的绝对值就是数轴上表示这个数的点与原点之间的距离。绝对值:│10│=10│-10│=10│ │叫做绝对值符号做一做|1.5|=1.5|-2.5|=2.5|0|=0|-1|=1一个正数的绝对值是___________;一个负数
的绝对值是它的__________________;0的
绝对值是_______.它本身相反数0思考:一个数的绝对值与这个数有什么关系?任何一个有理数的绝对值都是非负数.求绝对值的法则:
1.一个正数的绝对值是它本身;
2.零的绝对值是零;
3.一个负数的绝对值是它的相反数。|a|= a -a( 当a为正数 )(当a为0 )(当a为负数 )0|a|≥0(非负数)1:填空
|-2|= ,| |= ,
|0|= ,|+3|= ,
|-0.2|= ,|-8.3|= 。200.238.3小试身手 2.小测验:例2化简并计算: (1) ; (2)-|- 4|;
(3) . (4) |- 8|-|- 4|
3.想一想(1)? 绝对值是 12 的数有几个?
是什么?(2)? 绝对值是 0 的数有几个?是什么?(3)? 有没有绝对值是-3的数?为什么?绝对值是正数的数有两个,
他们是互为相反数4.绝对值小于5的整数有___个,分别是_______________.94,3,2,1,0,-1,-2,-3,-41.有理数的绝对值的意义.
代数意义:一个正数的绝对值是它本身;
零的绝对值是零;
一个负数的绝对值是它的相反数.
几何意义:到原点的距离理一理2.绝对值的性质:
3.绝对值与相反数的关系:
|a|≥0(非负性)互为相反数的两个数的绝对值相等;
绝对值相等,符号相反的两个数互为相反数;
若|a|=|b|,则a=b或者a=-b4.绝对值等于本身的数:
5.绝对值为非零数,则0和正数(非负数)原数有2个,且互为相反数1、若︱a ︱=3,则a =_____。探索思考2、若︱a-4 ︱+ ︱b︱=0,则a +b = _____。3、绝对值小于π的整数有_____,它们的和是多少?
甲车向东行驶了10公里和乙车向西行驶了10公里
(1)请用数轴表示这一过程
(记向东行驶的路程数为正)
情景引入:OBA010-1010105-5 例1:两位同学在书店购买书籍后坐出租车回家,
甲车向东行驶了10公里和乙车向西行驶了10公里
(1)请用数轴表示这一过程
(记向东行驶的路程数为正)
(2)若已知出租车前3公里收费10元,后面每
公里收费2元,还要加收每车次一元的燃油费,
问小明 和小华分别要付多少车费?
(3)所付的出租车费与行驶的方向有没有关系?(4)所付的出租车费与什么有关系?观察两辆出租车书店出发,分别向东、西方向行驶10km。OBA010-1010105-5思考:在数轴上这个路程表示什么?绝对值 在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值(absolute value).距离OBA010-1010105-5 一个数a的绝对值就是数轴上表示这个数的点与原点之间的距离。绝对值:│10│=10│-10│=10│ │叫做绝对值符号做一做|1.5|=1.5|-2.5|=2.5|0|=0|-1|=1一个正数的绝对值是___________;一个负数
的绝对值是它的__________________;0的
绝对值是_______.它本身相反数0思考:一个数的绝对值与这个数有什么关系?任何一个有理数的绝对值都是非负数.求绝对值的法则:
1.一个正数的绝对值是它本身;
2.零的绝对值是零;
3.一个负数的绝对值是它的相反数。|a|= a -a( 当a为正数 )(当a为0 )(当a为负数 )0|a|≥0(非负数)1:填空
|-2|= ,| |= ,
|0|= ,|+3|= ,
|-0.2|= ,|-8.3|= 。200.238.3小试身手 2.小测验:例2化简并计算: (1) ; (2)-|- 4|;
(3) . (4) |- 8|-|- 4|
3.想一想(1)? 绝对值是 12 的数有几个?
是什么?(2)? 绝对值是 0 的数有几个?是什么?(3)? 有没有绝对值是-3的数?为什么?绝对值是正数的数有两个,
他们是互为相反数4.绝对值小于5的整数有___个,分别是_______________.94,3,2,1,0,-1,-2,-3,-41.有理数的绝对值的意义.
代数意义:一个正数的绝对值是它本身;
零的绝对值是零;
一个负数的绝对值是它的相反数.
几何意义:到原点的距离理一理2.绝对值的性质:
3.绝对值与相反数的关系:
|a|≥0(非负性)互为相反数的两个数的绝对值相等;
绝对值相等,符号相反的两个数互为相反数;
若|a|=|b|,则a=b或者a=-b4.绝对值等于本身的数:
5.绝对值为非零数,则0和正数(非负数)原数有2个,且互为相反数1、若︱a ︱=3,则a =_____。探索思考2、若︱a-4 ︱+ ︱b︱=0,则a +b = _____。3、绝对值小于π的整数有_____,它们的和是多少?
