4.5多边形和圆的初步认识同步练习 (无答案) 2023—2024学年北师大版数学七年级上册
文档属性
| 名称 | 4.5多边形和圆的初步认识同步练习 (无答案) 2023—2024学年北师大版数学七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 187.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 00:00:00 | ||
图片预览

文档简介
4.5多边形和圆的初步认识
同步练习
一、单选题
1.过多边形的一个顶点共有3条对角线,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
2.七边形的对角线数量为( )条.
A.16 B.21 C.28 D.14
3.下列平面图形中不能镶嵌成一个平面图案的是( ).
A.任意三角形 B.任意四边形 C.正五边形 D.正六边形
4.用形状、大小完全相同的下列图形不能进行密铺的是( )
A.等腰三角形 B.平行四边形 C.正五边形 D.正六边形
5.一个多边形的内角和是外角的2倍,则这个多边形共有( )对角线
A.0条 B.2条 C.5条 D.9条
6.用下列一种多边形不能铺满地面的是( )
A.正方形 B.正十边形 C.正六边形 D.等边三角形
7.下列说法正确的是( )
A.不等边三角形一定是锐角三角形
B.三角形ABC也可表示为
C.各边都相等的多边形是正多边形
D.有两个内角分别为20°和50°的三角形一定是钝角三角形
8.在长125厘米,宽为 80厘米的长方形纸板上,你能最多画( )个半径为20厘米的圆.
A.12 B.7 C.6 D.8
9.六边形共有几条对角线( )
A.6 B.7 C.8 D.9
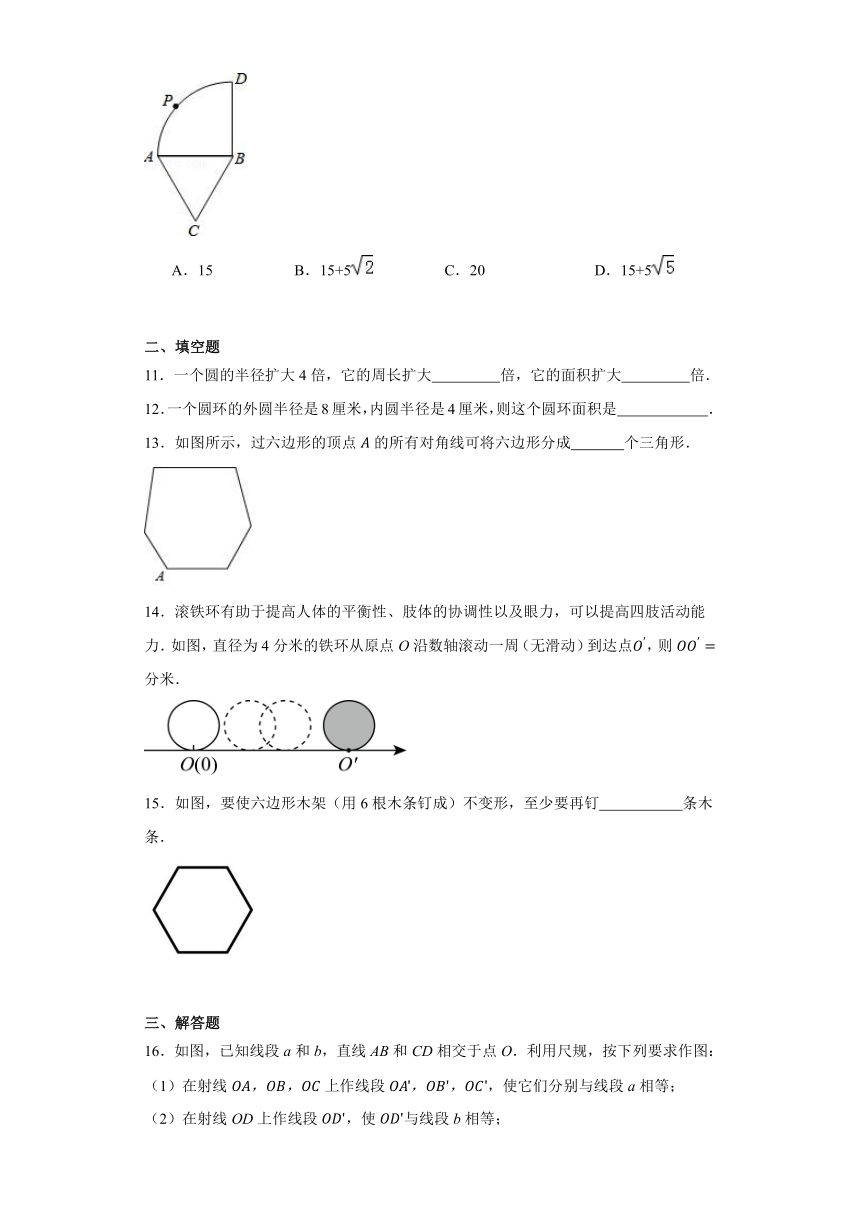
10.如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
A.15 B.15+5 C.20 D.15+5
二、填空题
11.一个圆的半径扩大4倍,它的周长扩大 倍,它的面积扩大 倍.
12.一个圆环的外圆半径是8厘米,内圆半径是4厘米,则这个圆环面积是 .
13.如图所示,过六边形的顶点的所有对角线可将六边形分成 个三角形.
14.滚铁环有助于提高人体的平衡性、肢体的协调性以及眼力,可以提高四肢活动能力.如图,直径为4分米的铁环从原点O沿数轴滚动一周(无滑动)到达点,则 分米.
15.如图,要使六边形木架(用6根木条钉成)不变形,至少要再钉 条木条.
三、解答题
16.如图,已知线段a和b,直线AB和CD相交于点O.利用尺规,按下列要求作图:
(1)在射线上作线段,使它们分别与线段a相等;
(2)在射线OD上作线段,使与线段b相等;
(3)连接.
你得到了一个怎样的图形?与同伴进行交流.
17.在下图中画一条线使五边形分成二个三角形
18.“乾隆通宝”是最具代表性的中国古代货币之一,为典型的圆形方孔形态,其钱径(货币直径)一般约厘米,厚厘米,重约克,中间方孔的边长为钱径的四分之一.图是一枚钱径为厘米的“乾隆通宝”钱币.(此题计算过程中圆周率取值均为3)
(1)请你在平面图中用作图的方式标出“乾隆通宝”钱币的中心点O.
(2)请你计算出平面图中阴影部分的面积是多少平方厘米?
(3)若将钱币绕过中心点O的竖直直线旋转一周(钱币厚度忽略不计),试求方孔旋转后得到的新图形的体积.
19.如图,长方形的长是,宽是,分别以、为圆心作扇形,用代数式表示阴影部分的周长和面积(结果中保留).
20.我们在用边长相同的正多边形进行平面镶嵌时,各正多边形重合的顶点叫拼接点,如图,就是拼接点.我们发现,各正多边形的以拼接点为顶点的内角之和为(注:若不能等于,则不能镶嵌).
图图
(1)如果我们只用一种边长相同的正多边形镶嵌,那么下面正多边形中,不能进行镶嵌的是______.(填序号)
正三角形;正方形;正五边形;正六边形.
(2)为了使镶嵌图案美丽多变,我们有时也可以用边长相同的两种正多边形进行镶嵌,如图,正三角形与正方形的平面镶嵌,在一个拼接点的周围有个正三角形和个正方形.
如果我们用边长相同的正三角形与正六边形进行镶嵌,求一个拼接点的周围有几个正三角形和几个正六边形;
我们也可以用边长相同的正五边形和正______边形进行镶嵌.
21.已知任意三角形的内角和为180°,试利用多边形中过某一顶点的对角线的条数,探求多边形内角和公式.
(1)如图1所示,一个四边形可以分成_______个三角形,于是四边形的内角和为_______;
(2)如图2所示,一个五边形可以分成_______个三角形,于是五边形的内角和为_______;
(3)按此规律,n()边形可以分成多少个三角形?n边形的内角和是多少度?
同步练习
一、单选题
1.过多边形的一个顶点共有3条对角线,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
2.七边形的对角线数量为( )条.
A.16 B.21 C.28 D.14
3.下列平面图形中不能镶嵌成一个平面图案的是( ).
A.任意三角形 B.任意四边形 C.正五边形 D.正六边形
4.用形状、大小完全相同的下列图形不能进行密铺的是( )
A.等腰三角形 B.平行四边形 C.正五边形 D.正六边形
5.一个多边形的内角和是外角的2倍,则这个多边形共有( )对角线
A.0条 B.2条 C.5条 D.9条
6.用下列一种多边形不能铺满地面的是( )
A.正方形 B.正十边形 C.正六边形 D.等边三角形
7.下列说法正确的是( )
A.不等边三角形一定是锐角三角形
B.三角形ABC也可表示为
C.各边都相等的多边形是正多边形
D.有两个内角分别为20°和50°的三角形一定是钝角三角形
8.在长125厘米,宽为 80厘米的长方形纸板上,你能最多画( )个半径为20厘米的圆.
A.12 B.7 C.6 D.8
9.六边形共有几条对角线( )
A.6 B.7 C.8 D.9
10.如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
A.15 B.15+5 C.20 D.15+5
二、填空题
11.一个圆的半径扩大4倍,它的周长扩大 倍,它的面积扩大 倍.
12.一个圆环的外圆半径是8厘米,内圆半径是4厘米,则这个圆环面积是 .
13.如图所示,过六边形的顶点的所有对角线可将六边形分成 个三角形.
14.滚铁环有助于提高人体的平衡性、肢体的协调性以及眼力,可以提高四肢活动能力.如图,直径为4分米的铁环从原点O沿数轴滚动一周(无滑动)到达点,则 分米.
15.如图,要使六边形木架(用6根木条钉成)不变形,至少要再钉 条木条.
三、解答题
16.如图,已知线段a和b,直线AB和CD相交于点O.利用尺规,按下列要求作图:
(1)在射线上作线段,使它们分别与线段a相等;
(2)在射线OD上作线段,使与线段b相等;
(3)连接.
你得到了一个怎样的图形?与同伴进行交流.
17.在下图中画一条线使五边形分成二个三角形
18.“乾隆通宝”是最具代表性的中国古代货币之一,为典型的圆形方孔形态,其钱径(货币直径)一般约厘米,厚厘米,重约克,中间方孔的边长为钱径的四分之一.图是一枚钱径为厘米的“乾隆通宝”钱币.(此题计算过程中圆周率取值均为3)
(1)请你在平面图中用作图的方式标出“乾隆通宝”钱币的中心点O.
(2)请你计算出平面图中阴影部分的面积是多少平方厘米?
(3)若将钱币绕过中心点O的竖直直线旋转一周(钱币厚度忽略不计),试求方孔旋转后得到的新图形的体积.
19.如图,长方形的长是,宽是,分别以、为圆心作扇形,用代数式表示阴影部分的周长和面积(结果中保留).
20.我们在用边长相同的正多边形进行平面镶嵌时,各正多边形重合的顶点叫拼接点,如图,就是拼接点.我们发现,各正多边形的以拼接点为顶点的内角之和为(注:若不能等于,则不能镶嵌).
图图
(1)如果我们只用一种边长相同的正多边形镶嵌,那么下面正多边形中,不能进行镶嵌的是______.(填序号)
正三角形;正方形;正五边形;正六边形.
(2)为了使镶嵌图案美丽多变,我们有时也可以用边长相同的两种正多边形进行镶嵌,如图,正三角形与正方形的平面镶嵌,在一个拼接点的周围有个正三角形和个正方形.
如果我们用边长相同的正三角形与正六边形进行镶嵌,求一个拼接点的周围有几个正三角形和几个正六边形;
我们也可以用边长相同的正五边形和正______边形进行镶嵌.
21.已知任意三角形的内角和为180°,试利用多边形中过某一顶点的对角线的条数,探求多边形内角和公式.
(1)如图1所示,一个四边形可以分成_______个三角形,于是四边形的内角和为_______;
(2)如图2所示,一个五边形可以分成_______个三角形,于是五边形的内角和为_______;
(3)按此规律,n()边形可以分成多少个三角形?n边形的内角和是多少度?
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
