1.1.2 直角三角形的边角关系 课件(共19张PPT)
文档属性
| 名称 | 1.1.2 直角三角形的边角关系 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 939.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 05:19:21 | ||
图片预览




文档简介
(共19张PPT)
第一章 直角三角形的边角关系
第1节 锐角三角形函数(2)
学习目标
1.理解并掌握锐角正弦、余弦的定义,并进行相关计算;(重点、难点)
2.在直角三角形中求正弦值、余弦值. (重点)
情景引入
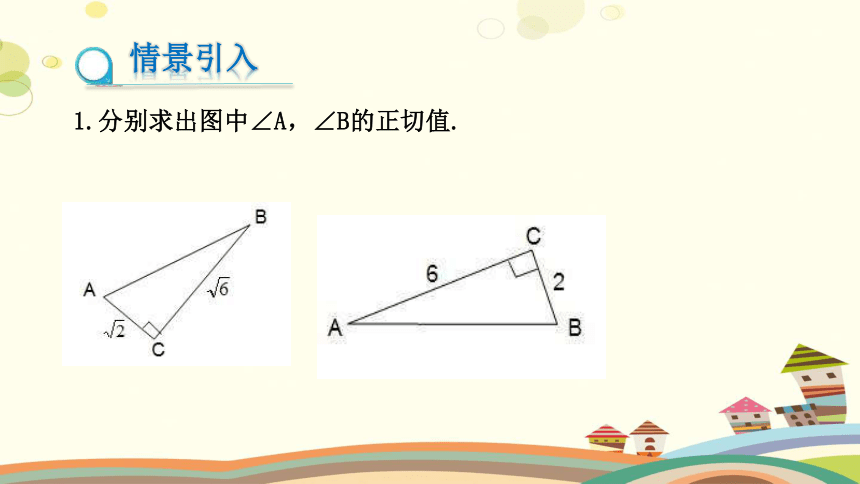
1.分别求出图中∠A,∠B的正切值.
A
B
C
∠A的对边
∠A的邻边
斜边
┌
如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其它边之间的比值也确定吗?
正弦的定义
1—
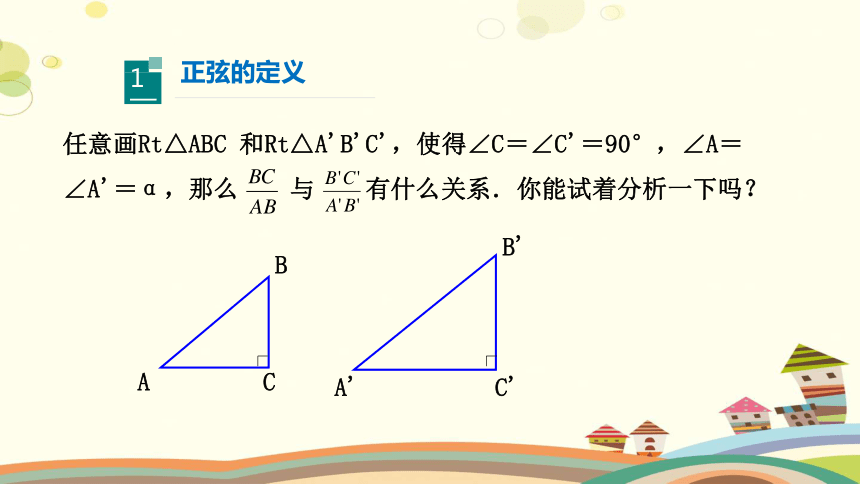
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.你能试着分析一下吗?
A
B
C
A'
B'
C'
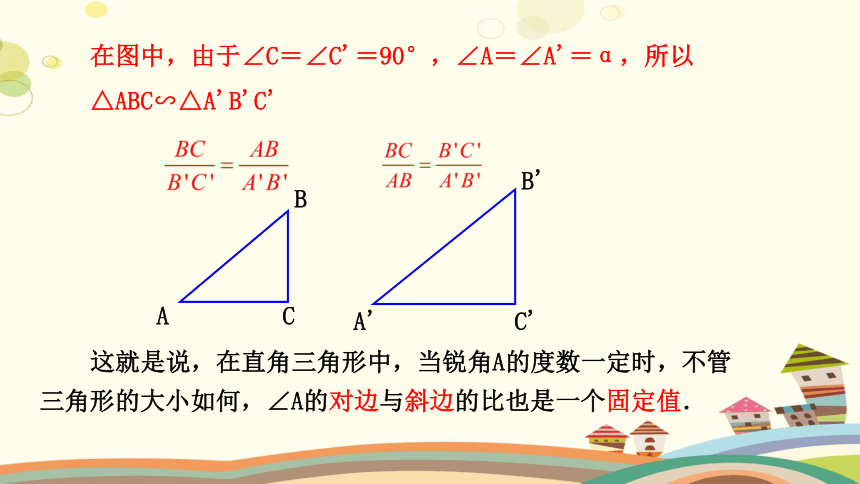
在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以△ABC∽△A'B'C'
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
A
B
C
A'
B'
C'
∠A的对边与斜边的比叫做∠A的正弦(sine),记作sinA , 即
∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
A
B
C
∠A的对边
∠A的邻边
斜边
┌
注意
1.sin A,cos A都是一个完整的符号,注意事项与正切类似.
2.sin A,cos A没有单位,其值与锐角A的大小有关,与所在直角三角形的边长无关.
3.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
A
B
C
∠A的对边
∠A的邻边
斜边
┌
锐角A的正弦、余弦、正切,都是∠A的三角函数.
例1.如图,在Rt△ABC中,∠B=90°,AC=200,sinA= 0.6, 求BC的长.
在Rt△ABC中,
∵
即
∴BC=200×0.6=120.
解:
A
B
C
典例精析
例2.在Rt △ ABC 中,∠ C=90°,∠ A,∠ B,∠ C 的对边分别用a,b,c 表示,其中a=5,b=12,求∠ A 的正弦值和∠ B 的余弦值.
典例精析
解:在Rt△ ABC中,由勾股定理,得
例3.如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.
5
5
6
A
B
C
┌
D
典例精析
A
C2
C1
B1
我们知道,梯子的倾斜程度与tanA有关系,tanA越大,梯子越陡,那么梯子的倾斜程度与sinA和cosA有关系吗?是怎样的关系?
sinA的值越大,梯子越陡;
cosA的值越小,梯子越陡.
典例精析
求:AB,sinB.
10
┐
A
B
C
例4.如图:在Rt△ABC中,∠C=90°,AC=10,
思考:我们再次发现sinA=cosB,其中的内在联系你可否掌握
随堂练习
1.在Rt△ABC中,若∠C=90°,AC=5,BC=12, 则sinA的值为_______.
2.在△ ABC 中,∠ C=90°,sin A= ,则tan B=( )
3.如图,在Rt△ABC中,∠C=90°,AB =10,BC=6,求sinA、cosA、tanA的值.
A
B
C
课堂总结
锐角三角函数定义:
A
B
C
∠A的对边a
┌
斜边c
∠A的邻边b
锐角三角函数的取值范围:
对于锐角A,有tan A>0,0<sin A<1,0<cos A<1.
第一章 直角三角形的边角关系
第1节 锐角三角形函数(2)
学习目标
1.理解并掌握锐角正弦、余弦的定义,并进行相关计算;(重点、难点)
2.在直角三角形中求正弦值、余弦值. (重点)
情景引入
1.分别求出图中∠A,∠B的正切值.
A
B
C
∠A的对边
∠A的邻边
斜边
┌
如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其它边之间的比值也确定吗?
正弦的定义
1—
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.你能试着分析一下吗?
A
B
C
A'
B'
C'
在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以△ABC∽△A'B'C'
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
A
B
C
A'
B'
C'
∠A的对边与斜边的比叫做∠A的正弦(sine),记作sinA , 即
∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
A
B
C
∠A的对边
∠A的邻边
斜边
┌
注意
1.sin A,cos A都是一个完整的符号,注意事项与正切类似.
2.sin A,cos A没有单位,其值与锐角A的大小有关,与所在直角三角形的边长无关.
3.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
A
B
C
∠A的对边
∠A的邻边
斜边
┌
锐角A的正弦、余弦、正切,都是∠A的三角函数.
例1.如图,在Rt△ABC中,∠B=90°,AC=200,sinA= 0.6, 求BC的长.
在Rt△ABC中,
∵
即
∴BC=200×0.6=120.
解:
A
B
C
典例精析
例2.在Rt △ ABC 中,∠ C=90°,∠ A,∠ B,∠ C 的对边分别用a,b,c 表示,其中a=5,b=12,求∠ A 的正弦值和∠ B 的余弦值.
典例精析
解:在Rt△ ABC中,由勾股定理,得
例3.如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.
5
5
6
A
B
C
┌
D
典例精析
A
C2
C1
B1
我们知道,梯子的倾斜程度与tanA有关系,tanA越大,梯子越陡,那么梯子的倾斜程度与sinA和cosA有关系吗?是怎样的关系?
sinA的值越大,梯子越陡;
cosA的值越小,梯子越陡.
典例精析
求:AB,sinB.
10
┐
A
B
C
例4.如图:在Rt△ABC中,∠C=90°,AC=10,
思考:我们再次发现sinA=cosB,其中的内在联系你可否掌握
随堂练习
1.在Rt△ABC中,若∠C=90°,AC=5,BC=12, 则sinA的值为_______.
2.在△ ABC 中,∠ C=90°,sin A= ,则tan B=( )
3.如图,在Rt△ABC中,∠C=90°,AB =10,BC=6,求sinA、cosA、tanA的值.
A
B
C
课堂总结
锐角三角函数定义:
A
B
C
∠A的对边a
┌
斜边c
∠A的邻边b
锐角三角函数的取值范围:
对于锐角A,有tan A>0,0<sin A<1,0<cos A<1.
