1.2 30°,45°,60°角的三角形函数值 课件(共20张PPT)
文档属性
| 名称 | 1.2 30°,45°,60°角的三角形函数值 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 05:17:59 | ||
图片预览






文档简介
(共20张PPT)
第一章 直角三角形的边角关系
第2节 30°,45°,60°角的三角形函数值
学习目标
1.运用三角函数的概念,自主探索,求出30°、 45°、60°角的三角函数值;(重点)
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用.(难点)
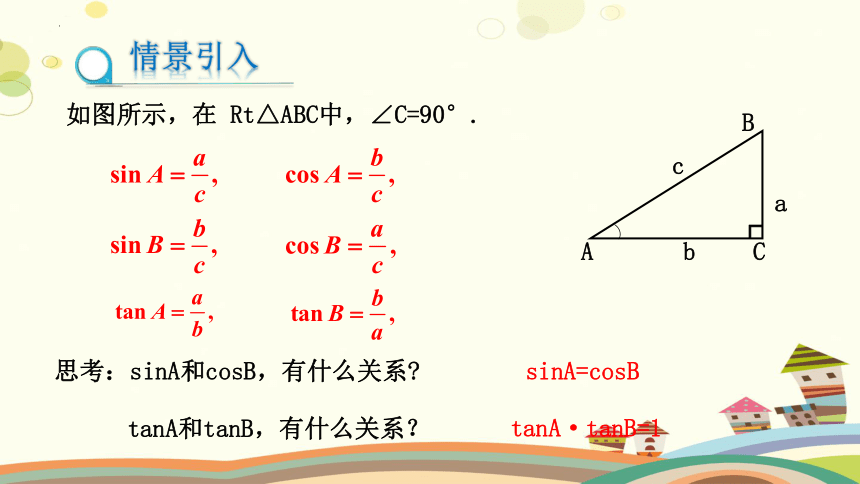
情景引入
b
A
B
C
a
┌
c
如图所示,在 Rt△ABC中,∠C=90°.
思考:sinA和cosB,有什么关系
sinA=cosB
tanA和tanB,有什么关系?
tanA·tanB=1
观察一副三角尺,其中有几个锐角?他们分别等于多少度?
思考:你能说说伴随你九个学年的这副三角尺所具有的特点和功能吗?
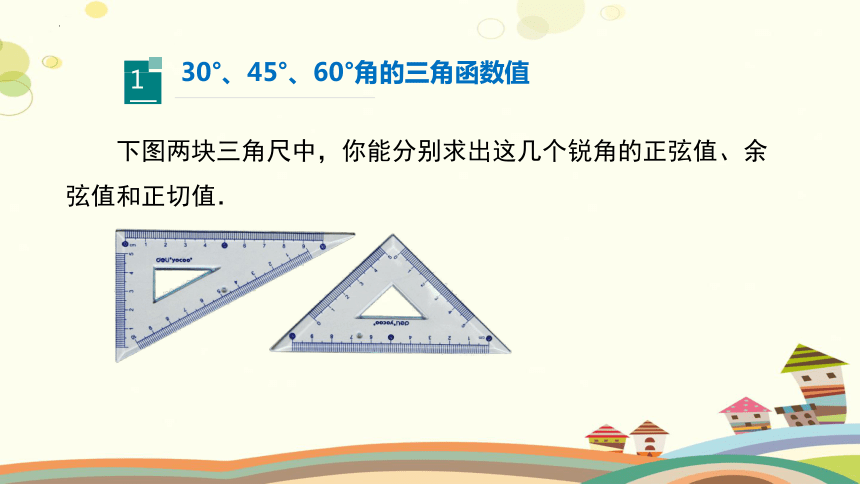
30°、45°、60°角的三角函数值
1—
下图两块三角尺中,你能分别求出这几个锐角的正弦值、余弦值和正切值.
(1)sin30°等于多少?你是怎样得到的?(2)cos30 °等于多少? tan30 °呢?
60°
30°
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
(1)60 °角的三角函数值分别是多少 你是怎样得到的
(2)45 °角的三角函数值分别是多少 你是怎样得到的
45°
45°
60°
30°
做一做
设两条直角边长为a,则斜边长=
45°
45°
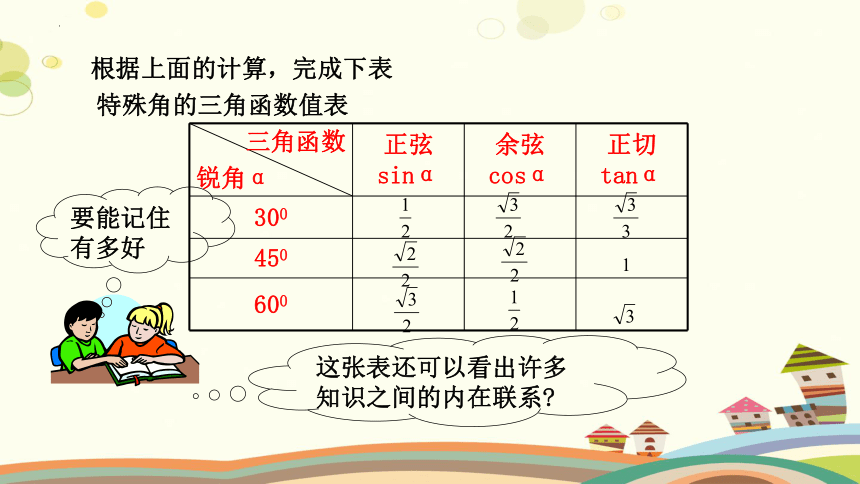
特殊角的三角函数值表
要能记住有多好
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
这张表还可以看出许多知识之间的内在联系
根据上面的计算,完成下表
(1)同角三角函数之间的关系.
①平方关系:sin2 A+cos2 A=1
②商除关系:∵
(2)互余两角的三角函数之间的关系.
sin A= cos( 90° - ∠ A);
cos A=sin( 90 ° - ∠ A) .
典例精析
例1.计算:
(1)sin 30° + cos 45°;
(2) sin260°+ cos260° — tan 45°.
(1) sin 30。+ cos 45。=
(2) sin260°+ cos260°- tan 45°
解:
sin260°表示(sin60°)2
cos260°表示(cos60°)2
典例精析
例2.一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60 °,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
O
B
A
D
C
2.5m
60°
解: 如图,由题意可知,∠AOD= ×60°=30 °,
OD = 2.5m,
∴ OC = OD·cos30 ° =2.5× ≈ 2.165(m).
∴ AC = 2.5-2.165 ≈ 0.34(m).
即最高位置与最低位置的高度差约为0.34m.
通过该表可以方便地知道30°,45°,60°角的三角函数值.它的另一个应用:如果已知一个锐角的三角函数值,就可以求出这个锐角的度数.例如:若sin θ= ,则锐角θ=45°.
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
典例精析
例3.如图,在Rt△ABC中,∠C=90°, ,求∠A的度数.
解: 如图,
A
B
C
典例精析
例4.在在△ ABC 中,∠ A,∠ B 均为锐角,且∠ A,∠ B 满足 试判断△ ABC 的形状,并说明理由 .
解:△ ABC 是直角三角形 .
理由如下:
又∵∠ A ,∠ B 均为锐角,
∴∠ A=60°,∠ B=30° .
∴∠A+∠B=60°+30°=90° .
∴△ ABC 是直角三角形 .
随堂练习
1.在Rt △ ABC 中,∠ C=90°,AB=2 ,AC= ,则∠ B 的度数为_____.
2.在△ABC中,∠A,∠B都是锐角,且sin A= ,
cos B= ,则△ABC的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
3.如图,在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B 两个凉亭之间的距离,现测得AC=30 m,BC=70 m,∠ CAB=120°,请计算A,B 两个凉亭之间的距离.
课堂总结
30° 45° 60°
sin A
cos A
tan A 1
特殊角的三角函数值:
第一章 直角三角形的边角关系
第2节 30°,45°,60°角的三角形函数值
学习目标
1.运用三角函数的概念,自主探索,求出30°、 45°、60°角的三角函数值;(重点)
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用.(难点)
情景引入
b
A
B
C
a
┌
c
如图所示,在 Rt△ABC中,∠C=90°.
思考:sinA和cosB,有什么关系
sinA=cosB
tanA和tanB,有什么关系?
tanA·tanB=1
观察一副三角尺,其中有几个锐角?他们分别等于多少度?
思考:你能说说伴随你九个学年的这副三角尺所具有的特点和功能吗?
30°、45°、60°角的三角函数值
1—
下图两块三角尺中,你能分别求出这几个锐角的正弦值、余弦值和正切值.
(1)sin30°等于多少?你是怎样得到的?(2)cos30 °等于多少? tan30 °呢?
60°
30°
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
(1)60 °角的三角函数值分别是多少 你是怎样得到的
(2)45 °角的三角函数值分别是多少 你是怎样得到的
45°
45°
60°
30°
做一做
设两条直角边长为a,则斜边长=
45°
45°
特殊角的三角函数值表
要能记住有多好
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
这张表还可以看出许多知识之间的内在联系
根据上面的计算,完成下表
(1)同角三角函数之间的关系.
①平方关系:sin2 A+cos2 A=1
②商除关系:∵
(2)互余两角的三角函数之间的关系.
sin A= cos( 90° - ∠ A);
cos A=sin( 90 ° - ∠ A) .
典例精析
例1.计算:
(1)sin 30° + cos 45°;
(2) sin260°+ cos260° — tan 45°.
(1) sin 30。+ cos 45。=
(2) sin260°+ cos260°- tan 45°
解:
sin260°表示(sin60°)2
cos260°表示(cos60°)2
典例精析
例2.一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60 °,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
O
B
A
D
C
2.5m
60°
解: 如图,由题意可知,∠AOD= ×60°=30 °,
OD = 2.5m,
∴ OC = OD·cos30 ° =2.5× ≈ 2.165(m).
∴ AC = 2.5-2.165 ≈ 0.34(m).
即最高位置与最低位置的高度差约为0.34m.
通过该表可以方便地知道30°,45°,60°角的三角函数值.它的另一个应用:如果已知一个锐角的三角函数值,就可以求出这个锐角的度数.例如:若sin θ= ,则锐角θ=45°.
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
典例精析
例3.如图,在Rt△ABC中,∠C=90°, ,求∠A的度数.
解: 如图,
A
B
C
典例精析
例4.在在△ ABC 中,∠ A,∠ B 均为锐角,且∠ A,∠ B 满足 试判断△ ABC 的形状,并说明理由 .
解:△ ABC 是直角三角形 .
理由如下:
又∵∠ A ,∠ B 均为锐角,
∴∠ A=60°,∠ B=30° .
∴∠A+∠B=60°+30°=90° .
∴△ ABC 是直角三角形 .
随堂练习
1.在Rt △ ABC 中,∠ C=90°,AB=2 ,AC= ,则∠ B 的度数为_____.
2.在△ABC中,∠A,∠B都是锐角,且sin A= ,
cos B= ,则△ABC的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
3.如图,在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B 两个凉亭之间的距离,现测得AC=30 m,BC=70 m,∠ CAB=120°,请计算A,B 两个凉亭之间的距离.
课堂总结
30° 45° 60°
sin A
cos A
tan A 1
特殊角的三角函数值:
