4.4 扇形的面积 课件(共17张PPT)
文档属性
| 名称 | 4.4 扇形的面积 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 421.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 05:26:35 | ||
图片预览






文档简介
(共17张PPT)
4.4 扇形的面积
沪教版六年级第一学期
第三章 比和比例
教学目标
(1)理解扇形的概念,掌握求扇形面积的计算公式;
(2)通过对实际问题的研究,初步认识数学与生活的联系,培养学生观察、概括、语言表达的能力,感受数学与生活的联系,树立数学学习的信心.
瞧一瞧,世界真奇妙!
新课学习
新课学习
1.扇形
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
半径
半径
弧
B
A
O
圆心角
问题1 下列各图中,那些图形是扇形?为什么
新课学习
A
B
O
C
O
A
B
C
O
A
(1)
(2)
(3)
是
B
O
C
A
B
(4)
新课学习
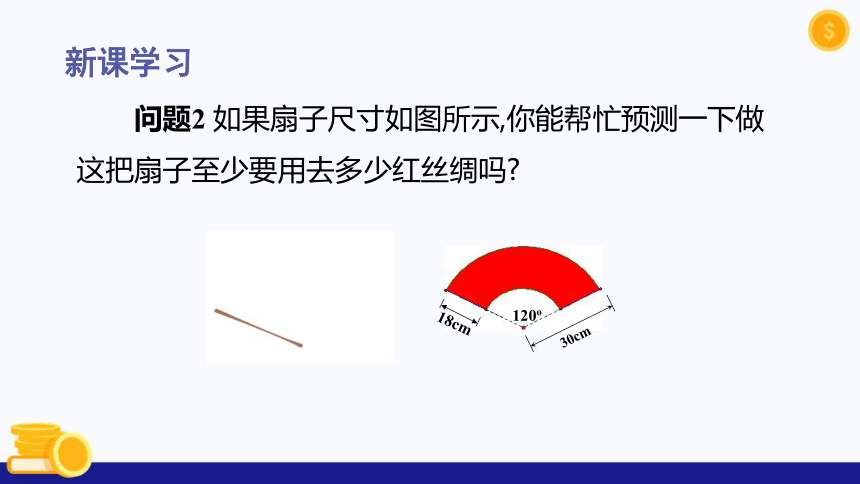
问题2 如果扇子尺寸如图所示,你能帮忙预测一下做这把扇子至少要用去多少红丝绸吗
30cm
18cm
120o
新课学习
问题3 扇形面积与哪些量有关呢?
圆心角不变,半径越大,扇形面积越大;
半径不变,圆心角越大,扇形面积越大;
扇形的面积和它的半径、圆心角的大小有关。
圆心角的大小与扇形
的面积有什么关系
扇形所在圆的半径大小与扇形的面积有什么关系
新课学习
问题3 扇形面积与哪些量有关呢?
1、圆心角为1°的扇形面积是圆面积的 .
2、圆心角为n 的扇形面积是圆面积的 .
新课学习
2.扇形面积计算公式
r
S扇 =
S圆
=
其中:r表示圆半径, n表示圆心角的度数,S表示面积
例题1 下面圆中的扇形面积各是圆面积的几分之几?
课堂例题
180
270
36
例题1 下面圆中的扇形面积各是圆面积的几分之几?
课堂例题
120
60
90
练习1 判断下列说法是否正确?
课堂例题
(1)扇形是圆的一部分,圆的一部分是扇形。( )
(2)两条半径和一条弧就能组成一个扇形。 ( )
(3)扇形的半径越大,面积也越大。 ( )
×
×
×
课堂例题
例题1 如图,一把展开的扇子的圆心角是120o,扇子的骨架长是30厘米. 求这把扇子展开所占的面积。
解:
n= 120°,r = 30cm
答:扇子展开所占面积约为942平方厘米。
新课学习
3.已知弧长和半径,求弧所在扇形的面积.
设组成扇形的半径为r,圆心角为no,弧长为l ,那么
新课学习
3.已知弧长和半径,求弧所在扇形的面积.
新课学习
思考3
若圆的半径不变,圆心角扩大n倍,则扇形面积扩大几倍?
若圆心角不变,圆的半径扩大n倍,则扇形面积扩大几倍?
课堂小结
一.扇形的概念
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形
二.扇形的面积
4.4 扇形的面积
沪教版六年级第一学期
第三章 比和比例
教学目标
(1)理解扇形的概念,掌握求扇形面积的计算公式;
(2)通过对实际问题的研究,初步认识数学与生活的联系,培养学生观察、概括、语言表达的能力,感受数学与生活的联系,树立数学学习的信心.
瞧一瞧,世界真奇妙!
新课学习
新课学习
1.扇形
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
半径
半径
弧
B
A
O
圆心角
问题1 下列各图中,那些图形是扇形?为什么
新课学习
A
B
O
C
O
A
B
C
O
A
(1)
(2)
(3)
是
B
O
C
A
B
(4)
新课学习
问题2 如果扇子尺寸如图所示,你能帮忙预测一下做这把扇子至少要用去多少红丝绸吗
30cm
18cm
120o
新课学习
问题3 扇形面积与哪些量有关呢?
圆心角不变,半径越大,扇形面积越大;
半径不变,圆心角越大,扇形面积越大;
扇形的面积和它的半径、圆心角的大小有关。
圆心角的大小与扇形
的面积有什么关系
扇形所在圆的半径大小与扇形的面积有什么关系
新课学习
问题3 扇形面积与哪些量有关呢?
1、圆心角为1°的扇形面积是圆面积的 .
2、圆心角为n 的扇形面积是圆面积的 .
新课学习
2.扇形面积计算公式
r
S扇 =
S圆
=
其中:r表示圆半径, n表示圆心角的度数,S表示面积
例题1 下面圆中的扇形面积各是圆面积的几分之几?
课堂例题
180
270
36
例题1 下面圆中的扇形面积各是圆面积的几分之几?
课堂例题
120
60
90
练习1 判断下列说法是否正确?
课堂例题
(1)扇形是圆的一部分,圆的一部分是扇形。( )
(2)两条半径和一条弧就能组成一个扇形。 ( )
(3)扇形的半径越大,面积也越大。 ( )
×
×
×
课堂例题
例题1 如图,一把展开的扇子的圆心角是120o,扇子的骨架长是30厘米. 求这把扇子展开所占的面积。
解:
n= 120°,r = 30cm
答:扇子展开所占面积约为942平方厘米。
新课学习
3.已知弧长和半径,求弧所在扇形的面积.
设组成扇形的半径为r,圆心角为no,弧长为l ,那么
新课学习
3.已知弧长和半径,求弧所在扇形的面积.
新课学习
思考3
若圆的半径不变,圆心角扩大n倍,则扇形面积扩大几倍?
若圆心角不变,圆的半径扩大n倍,则扇形面积扩大几倍?
课堂小结
一.扇形的概念
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形
二.扇形的面积
