5.4 二次函数与一元二次方程(第2课时)课件(共25张PPT)
文档属性
| 名称 | 5.4 二次函数与一元二次方程(第2课时)课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 00:00:00 | ||
图片预览




文档简介
第5章 二次函数
5.4 二次函数与一元二次方程(2)
第2课时 用逼近法求一元二次方程的近似解
学习目标
1.通过观察二次函数图像与x轴的交点坐标,能估算一元二次方程的近似根;
2.经历用图像法求一元二次方程的近似根的过程,进一步体会数形结合思想.
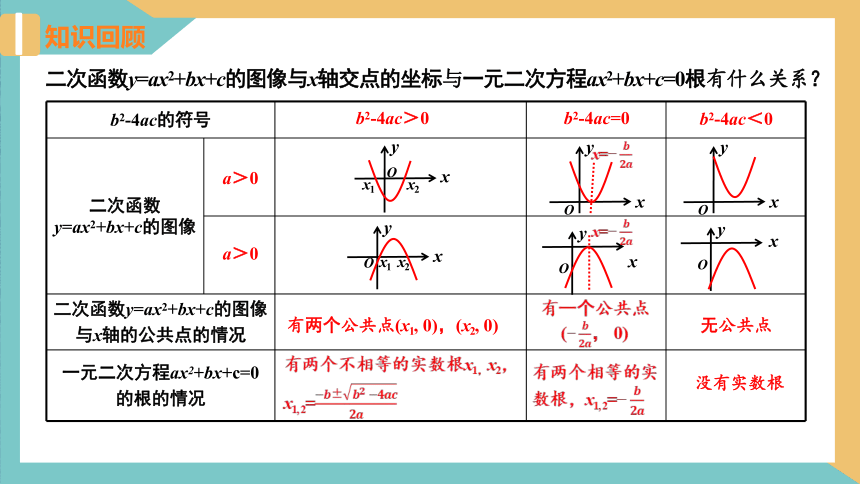
二次函数y=ax2+bx+c的图像与x轴交点的坐标与一元二次方程ax2+bx+c=0根有什么关系?
b2-4ac的符号
二次函数y=ax2+bx+c的图像
二次函数y=ax2+bx+c的图像
与x轴的公共点的情况
一元二次方程ax2+bx+c=0
的根的情况
a>0
a>0
b2-4ac>0
x
y
O
x1
x2
x
y
O
x1
x2
有两个公共点(x1, 0),(x2, 0)
有两个不相等的实数根x1,x2,
x1, 2=?????±?????????????????????????????
?
b2-4ac=0
x
y
O
x=?????????????
?
x
y
O
x=?????????????
?
有一个公共点(?????????????, 0)
?
有两个相等的实数根,x1, 2=?????????????
?
b2-4ac<0
x
y
O
x
y
O
无公共点
没有实数根
知识回顾
知识回顾
2.若方程ax2+bx+c=0的根为x1=-2和x2=3,则二次函数y=ax2+bx+c的图像与x轴交点坐标是__________________.
(-2,0)和(3,0)
1.抛物线y=0.5x2-x+3与x轴的交点情况是( )
A.两个交点 B.一个交点
C.没有交点 D.画出图像后才能说明
C
3.函数y=ax2+bx+c的图像如图,那么
方程ax2+bx+c=0的根是 ________________;
不等式ax2+bx+c>0的解集 是____________;
不等式ax2+bx+c<0的解集 是_________.
x1=-1, x2=3
x<-1或x>3
-1知识回顾
3
-1
O
x
y
-3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
观察与思考
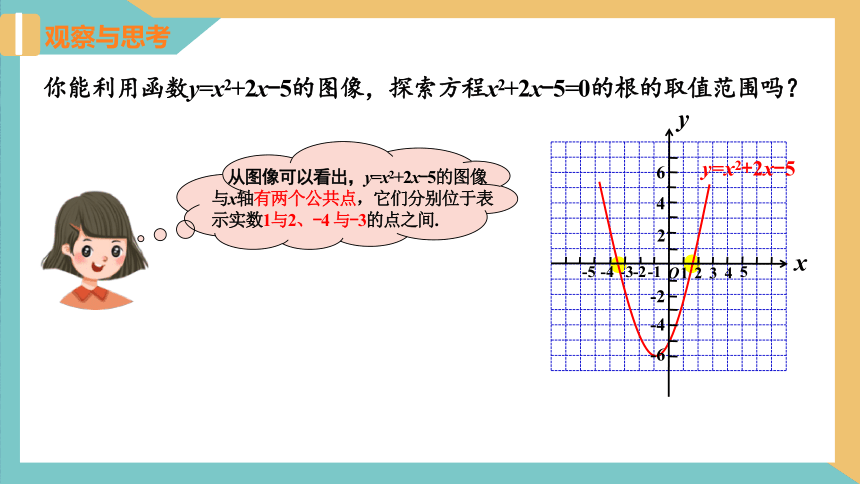
你能利用函数y=x2+2x-5的图像,探索方程x2+2x-5=0的根的取值范围吗?
1
2
-1
-4
O
2
4
x
y
3
-5
-6
6
y=x2+2x-5
-2
-4
从图像可以看出,y=x2+2x-5的图像与x轴有两个公共点,它们分别位于表示实数1与2、-4 与-3的点之间.
-2
4
5
{5940675A-B579-460E-94D1-54222C63F5DA}x
1.41
1.42
1.43
1.44
1.45
1.46
y
{5940675A-B579-460E-94D1-54222C63F5DA}-0.1919
-0.1436
-0.0951
-0.0464
0.0025
0.0516
{5940675A-B579-460E-94D1-54222C63F5DA}-1.59
-1.16
-0.71
-0.24
0.25
0.76
{5940675A-B579-460E-94D1-54222C63F5DA}x
1.1
1.2
1.3
1.4
1.5
1.6
y
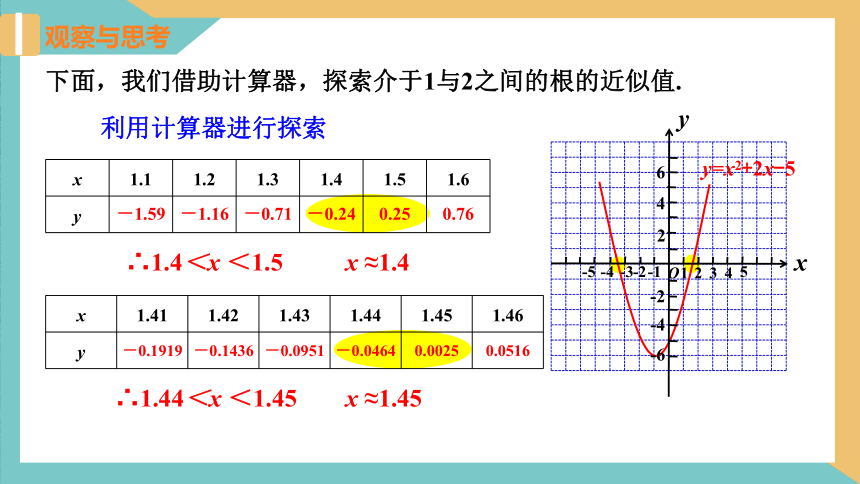
下面,我们借助计算器,探索介于1与2之间的根的近似值.
观察与思考
∴1.4<x <1.5
-3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
-1
-4
O
2
4
x
y
3
-5
-6
6
y=x2+2x-5
-2
-4
-2
4
5
∴1.44<x <1.45
x ≈1.4
x ≈1.45
利用计算器进行探索
{5940675A-B579-460E-94D1-54222C63F5DA}x
1.441
1.447
1.448
1.449
1.450
y
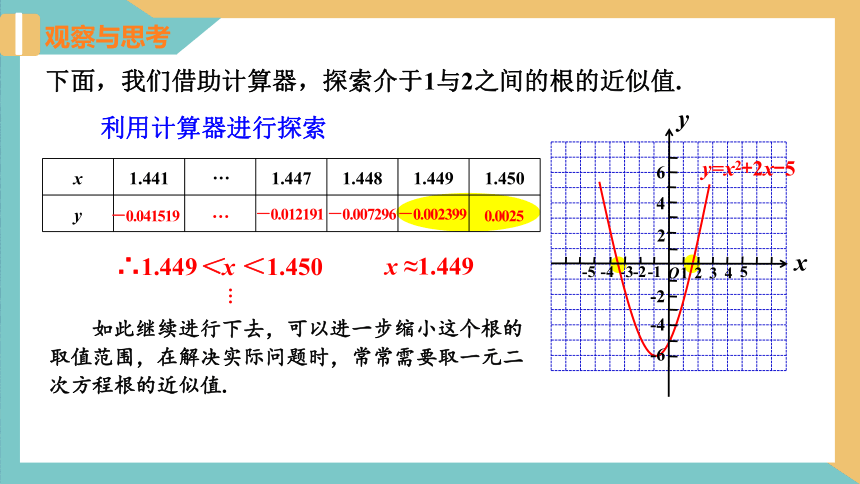
观察与思考
利用计算器进行探索
-3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
-1
-4
O
2
4
x
y
3
-5
-6
6
y=x2+2x-5
-2
-4
-2
4
5
…
-0.041519
…
-0.012191
-0.007296
-0.002399
0.0025
∴1.449<x <1.450
…
x ≈1.449
如此继续进行下去,可以进一步缩小这个根的取值范围,在解决实际问题时,常常需要取一元二次方程根的近似值.
下面,我们借助计算器,探索介于1与2之间的根的近似值.
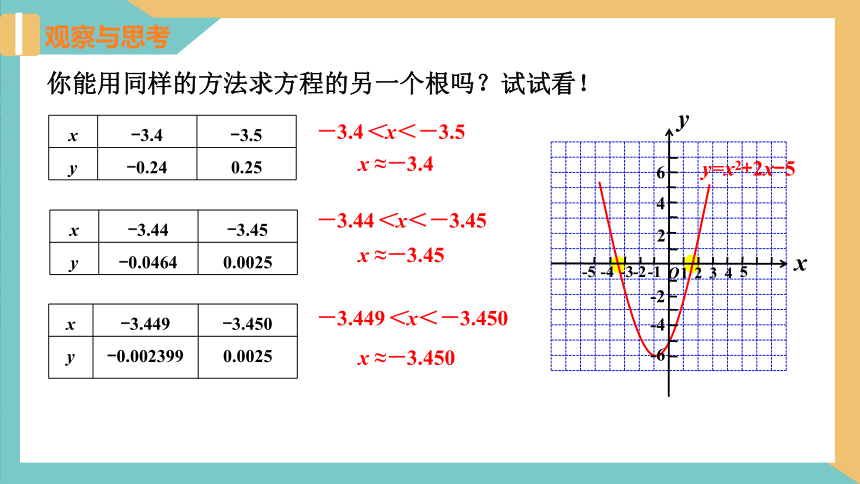
你能用同样的方法求方程的另一个根吗?试试看!
观察与思考
-3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
-1
-4
O
2
4
x
y
3
-5
-6
6
y=x2+2x-5
-2
-4
-2
4
5
-3.4<x<-3.5
x ≈-3.4
-3.44<x<-3.45
x ≈-3.45
{5940675A-B579-460E-94D1-54222C63F5DA}x
-3.449
-3.450
y
-0.002399
0.0025
-3.449<x<-3.450
x ≈-3.450
{5940675A-B579-460E-94D1-54222C63F5DA}x
-3.4
-3.5
y
-0.24
0.25
{5940675A-B579-460E-94D1-54222C63F5DA}x
-3.44
-3.45
y
-0.0464
0.0025
由函数图像我们发现一元二次方程的根两边的自变量对应的函数值的符号恰好相反,由此得到函数值相反的两个自变量之间一定含有一元二次方程的根.
归纳总结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
例 利用二次函数的图像求一元二次方程-x2+2x-3=-8的实数根(结果精确到0.1)
例题讲解
如图所示.左边的交点的横坐标在-2与-1之间,右边的交点的横坐标在3与4之间.
y=-x2+2x+5
x
2
1
4
O
3
-1
-2
5
1
2
y
3
6
-1
4
5
-2
解法1:利用函数y=-x2+2x+5求得方程-x2+2x-3=-8的近似根.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
例 利用二次函数的图像求一元二次方程-x2+2x-3=-8的实数根(结果精确到0.1)
例题讲解
由图像可知方程-x2+2x-3=-8的根是抛物线y=-x2+2x-3与直线y=-8的交点的横坐标,左边的交点的横坐标在-2与-1之间,右边的交点的横坐标在3与4之间.
y=-x2+2x-3
x
2
1
4
O
3
-1
-2
5
-5
-4
y
-3
-6
-7
-2
-1
-8
解法2:在平面直角坐标系内作出函数
y=-x2+2x-3的图像,如图所示.
1. 小明在学习了利用图像法求一元二次方程的近似根的知识后进行了尝试:在平面直角坐标系中作出二次函数y=x2+2x-10的图像,由图像可知,方程x2+2x-10=0有两个根,一个在-5和-4之间,另一个在2和3之间.利用计算器进行探索,得到下表,则方程的一个近似根是( )
x
-4.1
-4.2
-4.3
-4.4
y
-1.39
-0.76
-0.11
0.56
A. x≈-4.1 B. x≈-4.2 C. x≈-4.3 D. x≈-4.4
新知巩固
C
判断方程 ax2+bx+c =0 (a≠0,,a、b、c为常数)一个解x的范围是( )
A. 3C. 3.24{5940675A-B579-460E-94D1-54222C63F5DA} x
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.06
-0.02
0.03
0.09
C
2.根据下列表格的对应值:
新知巩固
新知巩固
3.已知二次函数y=ax2+bx+c的图像如图所示,则一元二次方程ax2+bx+c=0的近似根为( )
A. x1≈-2.1,x2≈0.1 B. x1≈-2.5,x2≈0.5
C. x1≈-2.9,x2≈0.9 D. x1≈-3,x2≈1
解:由图像可得二次函数y=ax2+bx+c图像的对称轴为x=-1,
而对称轴右侧图像与x轴交点到原点的距离约为0.5,
∴x2≈0.5;
又∵对称轴为x=-1,则????????+????????????=-1,
∴x1=2×(-1)-0.5=-2.5.
故x1≈-2.5,x2≈0.5.
?
B
O
x
1
-1
1
y
x2
x1
拓展提升
1.如图,过点(0,1)且平行于x轴的直线与二次函数y=ax2+bx+c(a>0)的图像的交点坐标为(1,1),(3,1),则不等式ax2+bx+c-1>0的解集为( )
C
A. x>1 B. 1<x<3
C. x<1或x>3 D. x>3
x
3
2
5
O
4
1
6
1
2
y
3
4
5
2.如图,直线y1=kx+b与抛物线y2=ax2+bx+c交于A(-1,m),B(4,n)两点,若kx+b<ax2+bx+c,则x的取值范围是( )A. x<-1 B. x>4 C.-1<x<4 D. x<-1或x>4
拓展提升
O
x
y
A
B
C
3. 已知二次函数y=ax2+bx+c与自变量x的部分对应值如下表:
x
…
-1
0
1
3
…
y
…
-3
1
3
1
…
现给出下列说法:①该函数图像开口向下;②该函数图像的对称轴为过点(1,0)且平行于y轴的直线;③当x=2时,y=3;④方程ax2+bx+c=-2的正根在3与4之间.其中正确的说法为________.(只需写出序号)
①③④
拓展提升
课堂小结
用逼近法求一元二次方程ax2+bx+c=0的近似解的一般步骤
(1)画出二次函数y=ax2+bx+c的图像
(2)确定抛物线与x轴的交点个数,看交点在哪两个数之间
(3)逐次用取中点的方法缩小探索范围
(4)根据精确度确定近似值
当堂检测
1.如下表给出了二次函数y=x2+2x-9中x,y的一些对应值,则可以估计一元二次方程x2+2x-9=0的一个近似解(精确到0.1)为( )
x
…
2
2.1
2.2
2.3
2.4
…
y
…
-1
-0.39
0.24
0.89
1.56
…
A.-4 B.2.2 C.-4.2 D.-4.3
B
当堂检测
2.已知二次函数y=ax2+bx+c中,y与x的部分对应值如下表:
x
…
1.1
1.2
1.3
1.4
1.5
1.6
…
y
…
-1.59
-1.16
-0.71
-0.24
0.25
0.76
…
则一元二次方程ax2+bx+c=0的一个解x满足条件( )A. 1.2<x<1.3 B. 1.3<x<1.4 C. 1.4<x<1.5 D. 1.5<x<1.6
C
(2)关于x的一元二次方程-x2+2x+k=0的的两个根是_______________;
当堂检测
3. 已知二次函数y=-x2+2x+k的部分图像如图所示,根据图像直接回答下列问题:
y
O
x
1
3
(3)不等式-x2+2x+k>0的解集为______________.
(1)函数图像与x轴的另一个交点的坐标为_______;
(3,0)
x1=-1,x2=3
-1<x<3
当堂检测
4.如图,二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)的图像的顶点为P(1,m),经过点A(2,1),有以下结论:
①a<0;
②abc>0;
③4a+2b+c=1;
④x>1时,y随x的增大而减小;
⑤对于任意实数t,总有at2+bt≤a+b;
其中正确的有___________.(填序号)
①③④⑤
O
x
y
A(2,1)
P(1,m)
1
2
-3
-4
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
当堂检测
5.在如图所示的平面直角坐标系中,作出函数y=x2-3x-2的图像,利用图像求:(1)方程x2-3x=2的近似解;
解:画出函数y=x2-3x-2的图像,
抛物线与x轴的交点坐标分别约是(-0.5,0),(3.5,0),所以方程x2-3x=2的实数根为
x1≈-0.5,x2≈3.5.
-1
O
2
4
x
y
3
-5
-6
6
y=x2-3x-2
-2
-4
-2
4
5
当堂检测
(2)方程x2-3x-2=2的近似解.(结果不是整数的精确到十分位)
抛物线与直线y=2的交点坐标分别是(-1,2),(4,2),
解:画出函数y=x2-3x-2的图像,
1
2
-3
-4
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
-1
O
2
4
x
y
3
-5
-6
6
y=x2-3x-2
-2
-4
-2
4
5
y=2
所以方程x2-3x-2=2的实数根为x1=-1,x2=4.
5.4 二次函数与一元二次方程(2)
第2课时 用逼近法求一元二次方程的近似解
学习目标
1.通过观察二次函数图像与x轴的交点坐标,能估算一元二次方程的近似根;
2.经历用图像法求一元二次方程的近似根的过程,进一步体会数形结合思想.
二次函数y=ax2+bx+c的图像与x轴交点的坐标与一元二次方程ax2+bx+c=0根有什么关系?
b2-4ac的符号
二次函数y=ax2+bx+c的图像
二次函数y=ax2+bx+c的图像
与x轴的公共点的情况
一元二次方程ax2+bx+c=0
的根的情况
a>0
a>0
b2-4ac>0
x
y
O
x1
x2
x
y
O
x1
x2
有两个公共点(x1, 0),(x2, 0)
有两个不相等的实数根x1,x2,
x1, 2=?????±?????????????????????????????
?
b2-4ac=0
x
y
O
x=?????????????
?
x
y
O
x=?????????????
?
有一个公共点(?????????????, 0)
?
有两个相等的实数根,x1, 2=?????????????
?
b2-4ac<0
x
y
O
x
y
O
无公共点
没有实数根
知识回顾
知识回顾
2.若方程ax2+bx+c=0的根为x1=-2和x2=3,则二次函数y=ax2+bx+c的图像与x轴交点坐标是__________________.
(-2,0)和(3,0)
1.抛物线y=0.5x2-x+3与x轴的交点情况是( )
A.两个交点 B.一个交点
C.没有交点 D.画出图像后才能说明
C
3.函数y=ax2+bx+c的图像如图,那么
方程ax2+bx+c=0的根是 ________________;
不等式ax2+bx+c>0的解集 是____________;
不等式ax2+bx+c<0的解集 是_________.
x1=-1, x2=3
x<-1或x>3
-1
3
-1
O
x
y
-3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
观察与思考
你能利用函数y=x2+2x-5的图像,探索方程x2+2x-5=0的根的取值范围吗?
1
2
-1
-4
O
2
4
x
y
3
-5
-6
6
y=x2+2x-5
-2
-4
从图像可以看出,y=x2+2x-5的图像与x轴有两个公共点,它们分别位于表示实数1与2、-4 与-3的点之间.
-2
4
5
{5940675A-B579-460E-94D1-54222C63F5DA}x
1.41
1.42
1.43
1.44
1.45
1.46
y
{5940675A-B579-460E-94D1-54222C63F5DA}-0.1919
-0.1436
-0.0951
-0.0464
0.0025
0.0516
{5940675A-B579-460E-94D1-54222C63F5DA}-1.59
-1.16
-0.71
-0.24
0.25
0.76
{5940675A-B579-460E-94D1-54222C63F5DA}x
1.1
1.2
1.3
1.4
1.5
1.6
y
下面,我们借助计算器,探索介于1与2之间的根的近似值.
观察与思考
∴1.4<x <1.5
-3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
-1
-4
O
2
4
x
y
3
-5
-6
6
y=x2+2x-5
-2
-4
-2
4
5
∴1.44<x <1.45
x ≈1.4
x ≈1.45
利用计算器进行探索
{5940675A-B579-460E-94D1-54222C63F5DA}x
1.441
1.447
1.448
1.449
1.450
y
观察与思考
利用计算器进行探索
-3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
-1
-4
O
2
4
x
y
3
-5
-6
6
y=x2+2x-5
-2
-4
-2
4
5
…
-0.041519
…
-0.012191
-0.007296
-0.002399
0.0025
∴1.449<x <1.450
…
x ≈1.449
如此继续进行下去,可以进一步缩小这个根的取值范围,在解决实际问题时,常常需要取一元二次方程根的近似值.
下面,我们借助计算器,探索介于1与2之间的根的近似值.
你能用同样的方法求方程的另一个根吗?试试看!
观察与思考
-3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
-1
-4
O
2
4
x
y
3
-5
-6
6
y=x2+2x-5
-2
-4
-2
4
5
-3.4<x<-3.5
x ≈-3.4
-3.44<x<-3.45
x ≈-3.45
{5940675A-B579-460E-94D1-54222C63F5DA}x
-3.449
-3.450
y
-0.002399
0.0025
-3.449<x<-3.450
x ≈-3.450
{5940675A-B579-460E-94D1-54222C63F5DA}x
-3.4
-3.5
y
-0.24
0.25
{5940675A-B579-460E-94D1-54222C63F5DA}x
-3.44
-3.45
y
-0.0464
0.0025
由函数图像我们发现一元二次方程的根两边的自变量对应的函数值的符号恰好相反,由此得到函数值相反的两个自变量之间一定含有一元二次方程的根.
归纳总结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
例 利用二次函数的图像求一元二次方程-x2+2x-3=-8的实数根(结果精确到0.1)
例题讲解
如图所示.左边的交点的横坐标在-2与-1之间,右边的交点的横坐标在3与4之间.
y=-x2+2x+5
x
2
1
4
O
3
-1
-2
5
1
2
y
3
6
-1
4
5
-2
解法1:利用函数y=-x2+2x+5求得方程-x2+2x-3=-8的近似根.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
例 利用二次函数的图像求一元二次方程-x2+2x-3=-8的实数根(结果精确到0.1)
例题讲解
由图像可知方程-x2+2x-3=-8的根是抛物线y=-x2+2x-3与直线y=-8的交点的横坐标,左边的交点的横坐标在-2与-1之间,右边的交点的横坐标在3与4之间.
y=-x2+2x-3
x
2
1
4
O
3
-1
-2
5
-5
-4
y
-3
-6
-7
-2
-1
-8
解法2:在平面直角坐标系内作出函数
y=-x2+2x-3的图像,如图所示.
1. 小明在学习了利用图像法求一元二次方程的近似根的知识后进行了尝试:在平面直角坐标系中作出二次函数y=x2+2x-10的图像,由图像可知,方程x2+2x-10=0有两个根,一个在-5和-4之间,另一个在2和3之间.利用计算器进行探索,得到下表,则方程的一个近似根是( )
x
-4.1
-4.2
-4.3
-4.4
y
-1.39
-0.76
-0.11
0.56
A. x≈-4.1 B. x≈-4.2 C. x≈-4.3 D. x≈-4.4
新知巩固
C
判断方程 ax2+bx+c =0 (a≠0,,a、b、c为常数)一个解x的范围是( )
A. 3
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.06
-0.02
0.03
0.09
C
2.根据下列表格的对应值:
新知巩固
新知巩固
3.已知二次函数y=ax2+bx+c的图像如图所示,则一元二次方程ax2+bx+c=0的近似根为( )
A. x1≈-2.1,x2≈0.1 B. x1≈-2.5,x2≈0.5
C. x1≈-2.9,x2≈0.9 D. x1≈-3,x2≈1
解:由图像可得二次函数y=ax2+bx+c图像的对称轴为x=-1,
而对称轴右侧图像与x轴交点到原点的距离约为0.5,
∴x2≈0.5;
又∵对称轴为x=-1,则????????+????????????=-1,
∴x1=2×(-1)-0.5=-2.5.
故x1≈-2.5,x2≈0.5.
?
B
O
x
1
-1
1
y
x2
x1
拓展提升
1.如图,过点(0,1)且平行于x轴的直线与二次函数y=ax2+bx+c(a>0)的图像的交点坐标为(1,1),(3,1),则不等式ax2+bx+c-1>0的解集为( )
C
A. x>1 B. 1<x<3
C. x<1或x>3 D. x>3
x
3
2
5
O
4
1
6
1
2
y
3
4
5
2.如图,直线y1=kx+b与抛物线y2=ax2+bx+c交于A(-1,m),B(4,n)两点,若kx+b<ax2+bx+c,则x的取值范围是( )A. x<-1 B. x>4 C.-1<x<4 D. x<-1或x>4
拓展提升
O
x
y
A
B
C
3. 已知二次函数y=ax2+bx+c与自变量x的部分对应值如下表:
x
…
-1
0
1
3
…
y
…
-3
1
3
1
…
现给出下列说法:①该函数图像开口向下;②该函数图像的对称轴为过点(1,0)且平行于y轴的直线;③当x=2时,y=3;④方程ax2+bx+c=-2的正根在3与4之间.其中正确的说法为________.(只需写出序号)
①③④
拓展提升
课堂小结
用逼近法求一元二次方程ax2+bx+c=0的近似解的一般步骤
(1)画出二次函数y=ax2+bx+c的图像
(2)确定抛物线与x轴的交点个数,看交点在哪两个数之间
(3)逐次用取中点的方法缩小探索范围
(4)根据精确度确定近似值
当堂检测
1.如下表给出了二次函数y=x2+2x-9中x,y的一些对应值,则可以估计一元二次方程x2+2x-9=0的一个近似解(精确到0.1)为( )
x
…
2
2.1
2.2
2.3
2.4
…
y
…
-1
-0.39
0.24
0.89
1.56
…
A.-4 B.2.2 C.-4.2 D.-4.3
B
当堂检测
2.已知二次函数y=ax2+bx+c中,y与x的部分对应值如下表:
x
…
1.1
1.2
1.3
1.4
1.5
1.6
…
y
…
-1.59
-1.16
-0.71
-0.24
0.25
0.76
…
则一元二次方程ax2+bx+c=0的一个解x满足条件( )A. 1.2<x<1.3 B. 1.3<x<1.4 C. 1.4<x<1.5 D. 1.5<x<1.6
C
(2)关于x的一元二次方程-x2+2x+k=0的的两个根是_______________;
当堂检测
3. 已知二次函数y=-x2+2x+k的部分图像如图所示,根据图像直接回答下列问题:
y
O
x
1
3
(3)不等式-x2+2x+k>0的解集为______________.
(1)函数图像与x轴的另一个交点的坐标为_______;
(3,0)
x1=-1,x2=3
-1<x<3
当堂检测
4.如图,二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)的图像的顶点为P(1,m),经过点A(2,1),有以下结论:
①a<0;
②abc>0;
③4a+2b+c=1;
④x>1时,y随x的增大而减小;
⑤对于任意实数t,总有at2+bt≤a+b;
其中正确的有___________.(填序号)
①③④⑤
O
x
y
A(2,1)
P(1,m)
1
2
-3
-4
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
当堂检测
5.在如图所示的平面直角坐标系中,作出函数y=x2-3x-2的图像,利用图像求:(1)方程x2-3x=2的近似解;
解:画出函数y=x2-3x-2的图像,
抛物线与x轴的交点坐标分别约是(-0.5,0),(3.5,0),所以方程x2-3x=2的实数根为
x1≈-0.5,x2≈3.5.
-1
O
2
4
x
y
3
-5
-6
6
y=x2-3x-2
-2
-4
-2
4
5
当堂检测
(2)方程x2-3x-2=2的近似解.(结果不是整数的精确到十分位)
抛物线与直线y=2的交点坐标分别是(-1,2),(4,2),
解:画出函数y=x2-3x-2的图像,
1
2
-3
-4
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
-1
O
2
4
x
y
3
-5
-6
6
y=x2-3x-2
-2
-4
-2
4
5
y=2
所以方程x2-3x-2=2的实数根为x1=-1,x2=4.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
