5.5 用二次函数解决问题(第1课时)课件(共25张PPT)
文档属性
| 名称 | 5.5 用二次函数解决问题(第1课时)课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 05:32:51 | ||
图片预览








文档简介
第5章 二次函数
5.5 用二次函数解决问题(1)
第1课时 利用二次函数解决销售利润最值问题
学习目标
1.学会运用二次函数的性质解决实际生活中利润的最大(小)值问题;
2.理解二次函数是刻画现实世界的一个有效的数学模型,了解建模思想在实际问题中广泛应用.
知识回顾
1. (1)二次函数 y=x2+4x化为顶点式为______________,当x=______时,有最____值,最_____值为_____;
y=(x+2)2-4
-2
小
小
-2
(2)二次函数 y=-x2+2x-3化为顶点式为________________,当x=_____时,有最_____值,最_____值为_____.
y=-(x-1)2-2
1
大
大
-2
知识回顾
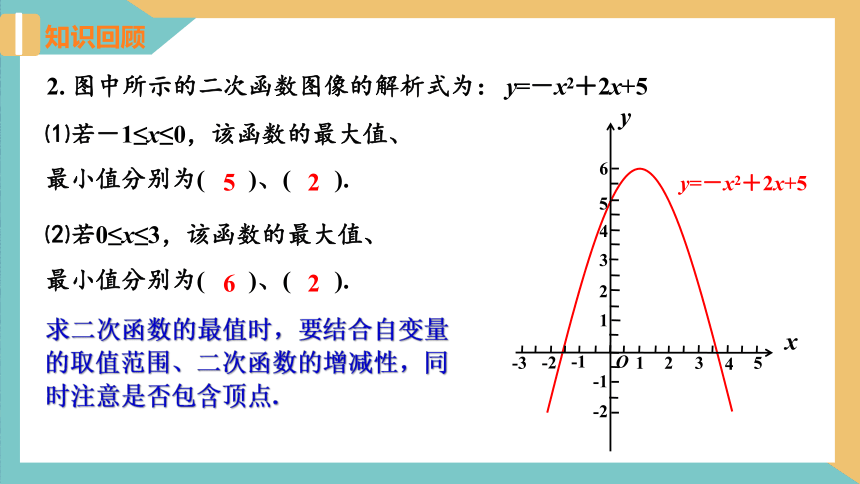
⑴若-1≤x≤0,该函数的最大值、最小值分别为( )、( ).
2. 图中所示的二次函数图像的解析式为: y=-x2+2x+5
5
2
y=-x2+2x+5
x
2
1
4
O
3
-1
-2
5
1
2
y
3
6
-1
4
5
-2
-3
⑵若0≤x≤3,该函数的最大值、最小值分别为( )、( ).
6
2
求二次函数的最值时,要结合自变量的取值范围、二次函数的增减性,同时注意是否包含顶点.
问题情境
某景区超市销售一种纪念品,现超市老板与员工讨论如何提高盈利.
薄利多销
提高售价
应该先做市场调研,
根据调研结果作出方案.
说说你的想法
讨论交流
若该超市销售的纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.
(1)当每件的销售价为52元时,该纪念品每天的销售数量为_______件;
解:(1)由题意,得
200-10×(52-50)
=200-20
=180(件).
180
讨论交流
若该超市销售的纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.
(2)当每件的销售价x为多少时,销售该纪念品每天获得的利润y最大?并求出最大利润.
解:(2)由题意,得
y=(x-40)[200-10(x-50)]
如何求二次函数的最值?
当每件的销售价为55元时,销售该纪念品每天获得的利润最大,最大利润为2250元.
=-10x2+1100x-28000
=-10(x-55)2+2250
问题1 某种粮大户去年种植优质水稻360亩,平均每亩收益440元.他计划今年多承租若干亩稻田.预计原360亩稻田平均每亩收益不变,新承租的稻田每增加1亩,其每亩平均收益比去年每亩平均收益少2元.该种粮大户今年应多承租多少亩稻田,才能使总收益最大?
分析:若设今年多承租x亩稻田,新承租的的稻田共收益___________元;根据题意可得函数表达式:______________________ .
x(440-2x)
y=440×360+x(440-2x)
例题讲解
问题1 某种粮大户去年种植优质水稻360亩,平均每亩收益440元.他计划今年多承租若干亩稻田.预计原360亩稻田平均每亩收益不变,新承租的稻田每增加1亩,其每亩平均收益比去年每亩平均收益少2元.该种粮大户今年应多承租多少亩稻田,才能使总收益最大?
y=440×360+x(440-2x)
=-2x2+440x+158400
=-2(x-110)2+182600
答:该种粮大户今年应多承租110亩水稻,才能使总收益最大,最大收益是182600元.
解:设该种粮大户的今年总收益为y元.
∵a=-2<0,∴函数有最大值,
当x=110时,y最大=182600
例题讲解
变式 某种粮大户去年种植优质水稻360亩, 今年计划增加承租x(100≤x≤150)亩,预计,原种植的360亩水稻今年每亩可收益440元,新增加地今年每亩的收益为(440-2x)元,试问:该种植大户今年要增加承租_____亩水稻,才能使总收益是181800元.
例题讲解
y=440×360+x(440-2x)
=-2x2+440x+158400
=-2(x-110)2+182600
答:要承租130亩水稻,才能使总收益为181800元.
解:设该种粮大户的今年总收益为y元.
当y=181800时,
-2(x-110)2+182600=181800
x1=90<100(舍去),x2=130
注意自变量的取值范围
130
例题讲解
问题2 某鱼塘里饲养了鱼苗10千尾.预计平均每千尾鱼的产量为1000kg. 若再向该鱼塘里投放鱼苗,每多投放鱼苗1千尾,每千尾鱼的产量将减少50kg.应再投放鱼苗多少千尾才能使总产量最大?最大总产量是多少?
分析:如果今年向鱼塘投放鱼苗x千尾,那么鱼塘里共有鱼苗 ______千尾,每千尾鱼的产量为___________kg. 根据题意可得函数表达式:___________________.
(10+x)
(1000-50x)
y=(1000-50x)(10+x)
解:设向鱼塘里再投放鱼苗x千尾,总产量为ykg,则
y=(1000-50x)(10+x)=-50(x-5)2+11250.
当x=5时,y的值最大,最大值是11250.
答:应再投放鱼苗5千尾才能使总产量最大,最大总产量为11250kg.
变式 某市某水产养殖中心2022年鱼塘饲养鱼苗10千尾,平均每千尾鱼的产量为1000千克,2023年计划继续向鱼塘投放鱼苗,每多投放鱼苗1千尾,每千尾的产量将减少50千克.2023年应再投放鱼苗多少千尾,可以使总产量达到10450千克?
例题讲解
解:设2023年再投放鱼苗x千尾,总产量为ykg,则
y=(1000-50x)(10+x)=-50(x-5)2+11250.
当y=10450时,-50(x-5)2+11250=10450
解得x1=1,x2=9.
答:2023年应投放鱼苗1千尾或9千尾,可以使总产量达到10450千克.
归纳总结
(1)审:找出问题中的变量和常量,分析问题中的变量之间的等量关系;
(2)设:设出适当的未知数;
(3)列:用二次函数表示出变量和常量之间的关系,列出二次函数的表达式;
(4)解:依据已知条件,借助二次函数的表达式、图像和性质等求解
(注意实际问题中自变量的取值范围);
(5)验:检验结果,得出符合实际意义的结论;
(6)答:写出答案.
用二次函数解决实际问题的一般步骤:
新知巩固
1. 某商场以每件42元的价格购进一种服装,由试销知,每天的销量t(件)与每件的销售价 x(元)之间的函数关系为t=204-3x.
(1)试写出每天销售这种服装的毛利润y(元)与每件销售价x(元)之间的函数表达式(毛利润=销售价一进货价);
(2)每件销售价多少元才能使每天的毛利润最大?最大毛利润是多少?
解:(1)y=(x-42)(204-3x);
(2)y=(x-42)(204-3x)=-3x2+330x-8568.
当x=55时,y的值最大,最大值是507.
答:销售价定为55元才能使每天的毛利润最大,最大毛利润是507元.
新知巩固
2. 某汽车出租公司以每辆汽车月租费3000元,100辆汽车可以全部租出若每辆汽车的月租费每增加50元,则将少租出1辆汽车.已知每辆租出的汽车支付月维护费200元,问每月租出多少辆汽车时,该出租公司的月收益最大?最大月收益是多少?
解:设每月租出x辆汽车,月收益为y元,则
y=[3000+50(100-x)-200]x=-50(x-78)2+304200.
当x=78时,y的值最大,最大值是304200.
答:每月租出78辆汽车时,该出租公司的月收益最大,最大月收益
是304200元.
课堂小结
利用二次函数解决销售利润最值问题
数学问题
构建二次函数模型
用二次函数解决实际问题的一般步骤:
审设列解验答
当堂检测
1.一枚炮弹射出x秒后的高度为y米,且y与x之间的关系为y=ax2+bx+c
(a≠0),若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )A.第8秒 B.第10秒 C.第12秒 D.第15秒
C
2.某超市销售一种商品,发现一周的利润y(元)与销售单价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,销售单价只能为15≤x≤22,那么这种商品一周可获得的最大利润是( )A.1558元 B.1550元 C.1508元 D.20元
A
当堂检测
3.某种商品的价格是2元,准备进行两次降价.如果每次降价的百分率都是x,经过两次降价后的价格y(单位:元)随每次降价的百分率x的变化而变化,则y关于x的函数表达式是( )A.y=2(x+1)2 B.y=2(1-x)2 C.y=(x+1)2 D.y=(x-1)2
B
4.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售价为x元,则可卖出(350-10x)件,则商店所获得的利润y(元)与每件商品售价x(元)之间的函数表达式为( )A.y=-10x2-560x+7350 B.y=-10x2+560x-7350C.y=-10x2+350x D.y=-10x2+350x-7350
B
当堂检测
5. 某产品的进货单价为每件90元,按100元一件出售时,每周能售出500件.若每件涨价1元,则每周销售量就减少10件,则该产品每周能获得的最大利润为__________.
9000元
6.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅游团的人数每增加一人,每人的单价就降低10元,若这个旅行社要获得最大营业额,则这个旅游团的人数是_____.
55
当堂检测
7.某产品每件的成本价是120元,试销阶段,每件产品的销售价格x(元)与产品的日销售量y(件)之间的关系如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}x(元)
130
150
165
y(件)
70
50
35
(1)则y与x的函数关系式为__________;
y=-x+200
若销售量y是销售价格x的一次函数.
解:设销售利润为W元,则W=(x-120)y=(x-120)(-x+200)
=-x2+320x-24000=-(x-160)2+1600,∵-1<0,∴当x=160时,W取最大值,最大值为1600.
答:每件产品的销售价格定为160元时,此时每日的销售利润最大,最大利润是1600元.
当堂检测
(2)若要获得最大的销售利润,每件产品的销售价格定为多少元?此时每日的销售利润是多少?
当堂检测
8.王大伯决定销售一批风筝,经市场调研:蝙蝠形风筝每个进价为10元,当每个售价为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)求蝙蝠形风筝销售量y(个)与每个售价x(元)之间的函数表达式(12≤x≤30);
解:根据题意,得y=180-10(x-12)=-10x+300(12≤x≤30).
当堂检测
(2)当每个风筝的售价定为多少时,王大伯获得的利润最大,最大利润是多少?
解:设王大伯获得的利润为W元,则
W=(x-10)y=-10x2+400x-3000=-10(x-20)2+1000,∵-10<0,∴当x=20时,W取最大值,最大值为1000.
答:当每个风筝的售价定为20元时,王大伯获得的利润最大,最大利润是1000元.
当堂检测
9. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,经市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数表达式,并写出自变量x的取值范围;
x(元/件)
y(件)
10
16
24
30
O
解:(1)设y与x之间的函数关系式为y=kx+b,把(10,30),(16,24)代入,得????????????+????=????????,????????????+????=????????,
解得????=-????????=????????.∴y与x之间的函数表达式为y=-x+40(10≤x≤16).
?
当堂检测
(2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出当销售价为多少元/件时,每天的销售利润最大,最大利润是多少.
解:(2)W=(x-10)(-x+40)=-x2+50x-400(10≤x≤16).
∵W=-x2+50x-400=-(x-25)2+225,
函数图像的对称轴是直线x=25,在对称轴的左侧,y随着x的增大而增大.∵10≤x≤16,∴当x=16时,W最大,为144.即当销售价为16元/件时,每天的销售利润最大,最大利润是144元.
5.5 用二次函数解决问题(1)
第1课时 利用二次函数解决销售利润最值问题
学习目标
1.学会运用二次函数的性质解决实际生活中利润的最大(小)值问题;
2.理解二次函数是刻画现实世界的一个有效的数学模型,了解建模思想在实际问题中广泛应用.
知识回顾
1. (1)二次函数 y=x2+4x化为顶点式为______________,当x=______时,有最____值,最_____值为_____;
y=(x+2)2-4
-2
小
小
-2
(2)二次函数 y=-x2+2x-3化为顶点式为________________,当x=_____时,有最_____值,最_____值为_____.
y=-(x-1)2-2
1
大
大
-2
知识回顾
⑴若-1≤x≤0,该函数的最大值、最小值分别为( )、( ).
2. 图中所示的二次函数图像的解析式为: y=-x2+2x+5
5
2
y=-x2+2x+5
x
2
1
4
O
3
-1
-2
5
1
2
y
3
6
-1
4
5
-2
-3
⑵若0≤x≤3,该函数的最大值、最小值分别为( )、( ).
6
2
求二次函数的最值时,要结合自变量的取值范围、二次函数的增减性,同时注意是否包含顶点.
问题情境
某景区超市销售一种纪念品,现超市老板与员工讨论如何提高盈利.
薄利多销
提高售价
应该先做市场调研,
根据调研结果作出方案.
说说你的想法
讨论交流
若该超市销售的纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.
(1)当每件的销售价为52元时,该纪念品每天的销售数量为_______件;
解:(1)由题意,得
200-10×(52-50)
=200-20
=180(件).
180
讨论交流
若该超市销售的纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.
(2)当每件的销售价x为多少时,销售该纪念品每天获得的利润y最大?并求出最大利润.
解:(2)由题意,得
y=(x-40)[200-10(x-50)]
如何求二次函数的最值?
当每件的销售价为55元时,销售该纪念品每天获得的利润最大,最大利润为2250元.
=-10x2+1100x-28000
=-10(x-55)2+2250
问题1 某种粮大户去年种植优质水稻360亩,平均每亩收益440元.他计划今年多承租若干亩稻田.预计原360亩稻田平均每亩收益不变,新承租的稻田每增加1亩,其每亩平均收益比去年每亩平均收益少2元.该种粮大户今年应多承租多少亩稻田,才能使总收益最大?
分析:若设今年多承租x亩稻田,新承租的的稻田共收益___________元;根据题意可得函数表达式:______________________ .
x(440-2x)
y=440×360+x(440-2x)
例题讲解
问题1 某种粮大户去年种植优质水稻360亩,平均每亩收益440元.他计划今年多承租若干亩稻田.预计原360亩稻田平均每亩收益不变,新承租的稻田每增加1亩,其每亩平均收益比去年每亩平均收益少2元.该种粮大户今年应多承租多少亩稻田,才能使总收益最大?
y=440×360+x(440-2x)
=-2x2+440x+158400
=-2(x-110)2+182600
答:该种粮大户今年应多承租110亩水稻,才能使总收益最大,最大收益是182600元.
解:设该种粮大户的今年总收益为y元.
∵a=-2<0,∴函数有最大值,
当x=110时,y最大=182600
例题讲解
变式 某种粮大户去年种植优质水稻360亩, 今年计划增加承租x(100≤x≤150)亩,预计,原种植的360亩水稻今年每亩可收益440元,新增加地今年每亩的收益为(440-2x)元,试问:该种植大户今年要增加承租_____亩水稻,才能使总收益是181800元.
例题讲解
y=440×360+x(440-2x)
=-2x2+440x+158400
=-2(x-110)2+182600
答:要承租130亩水稻,才能使总收益为181800元.
解:设该种粮大户的今年总收益为y元.
当y=181800时,
-2(x-110)2+182600=181800
x1=90<100(舍去),x2=130
注意自变量的取值范围
130
例题讲解
问题2 某鱼塘里饲养了鱼苗10千尾.预计平均每千尾鱼的产量为1000kg. 若再向该鱼塘里投放鱼苗,每多投放鱼苗1千尾,每千尾鱼的产量将减少50kg.应再投放鱼苗多少千尾才能使总产量最大?最大总产量是多少?
分析:如果今年向鱼塘投放鱼苗x千尾,那么鱼塘里共有鱼苗 ______千尾,每千尾鱼的产量为___________kg. 根据题意可得函数表达式:___________________.
(10+x)
(1000-50x)
y=(1000-50x)(10+x)
解:设向鱼塘里再投放鱼苗x千尾,总产量为ykg,则
y=(1000-50x)(10+x)=-50(x-5)2+11250.
当x=5时,y的值最大,最大值是11250.
答:应再投放鱼苗5千尾才能使总产量最大,最大总产量为11250kg.
变式 某市某水产养殖中心2022年鱼塘饲养鱼苗10千尾,平均每千尾鱼的产量为1000千克,2023年计划继续向鱼塘投放鱼苗,每多投放鱼苗1千尾,每千尾的产量将减少50千克.2023年应再投放鱼苗多少千尾,可以使总产量达到10450千克?
例题讲解
解:设2023年再投放鱼苗x千尾,总产量为ykg,则
y=(1000-50x)(10+x)=-50(x-5)2+11250.
当y=10450时,-50(x-5)2+11250=10450
解得x1=1,x2=9.
答:2023年应投放鱼苗1千尾或9千尾,可以使总产量达到10450千克.
归纳总结
(1)审:找出问题中的变量和常量,分析问题中的变量之间的等量关系;
(2)设:设出适当的未知数;
(3)列:用二次函数表示出变量和常量之间的关系,列出二次函数的表达式;
(4)解:依据已知条件,借助二次函数的表达式、图像和性质等求解
(注意实际问题中自变量的取值范围);
(5)验:检验结果,得出符合实际意义的结论;
(6)答:写出答案.
用二次函数解决实际问题的一般步骤:
新知巩固
1. 某商场以每件42元的价格购进一种服装,由试销知,每天的销量t(件)与每件的销售价 x(元)之间的函数关系为t=204-3x.
(1)试写出每天销售这种服装的毛利润y(元)与每件销售价x(元)之间的函数表达式(毛利润=销售价一进货价);
(2)每件销售价多少元才能使每天的毛利润最大?最大毛利润是多少?
解:(1)y=(x-42)(204-3x);
(2)y=(x-42)(204-3x)=-3x2+330x-8568.
当x=55时,y的值最大,最大值是507.
答:销售价定为55元才能使每天的毛利润最大,最大毛利润是507元.
新知巩固
2. 某汽车出租公司以每辆汽车月租费3000元,100辆汽车可以全部租出若每辆汽车的月租费每增加50元,则将少租出1辆汽车.已知每辆租出的汽车支付月维护费200元,问每月租出多少辆汽车时,该出租公司的月收益最大?最大月收益是多少?
解:设每月租出x辆汽车,月收益为y元,则
y=[3000+50(100-x)-200]x=-50(x-78)2+304200.
当x=78时,y的值最大,最大值是304200.
答:每月租出78辆汽车时,该出租公司的月收益最大,最大月收益
是304200元.
课堂小结
利用二次函数解决销售利润最值问题
数学问题
构建二次函数模型
用二次函数解决实际问题的一般步骤:
审设列解验答
当堂检测
1.一枚炮弹射出x秒后的高度为y米,且y与x之间的关系为y=ax2+bx+c
(a≠0),若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )A.第8秒 B.第10秒 C.第12秒 D.第15秒
C
2.某超市销售一种商品,发现一周的利润y(元)与销售单价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,销售单价只能为15≤x≤22,那么这种商品一周可获得的最大利润是( )A.1558元 B.1550元 C.1508元 D.20元
A
当堂检测
3.某种商品的价格是2元,准备进行两次降价.如果每次降价的百分率都是x,经过两次降价后的价格y(单位:元)随每次降价的百分率x的变化而变化,则y关于x的函数表达式是( )A.y=2(x+1)2 B.y=2(1-x)2 C.y=(x+1)2 D.y=(x-1)2
B
4.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售价为x元,则可卖出(350-10x)件,则商店所获得的利润y(元)与每件商品售价x(元)之间的函数表达式为( )A.y=-10x2-560x+7350 B.y=-10x2+560x-7350C.y=-10x2+350x D.y=-10x2+350x-7350
B
当堂检测
5. 某产品的进货单价为每件90元,按100元一件出售时,每周能售出500件.若每件涨价1元,则每周销售量就减少10件,则该产品每周能获得的最大利润为__________.
9000元
6.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅游团的人数每增加一人,每人的单价就降低10元,若这个旅行社要获得最大营业额,则这个旅游团的人数是_____.
55
当堂检测
7.某产品每件的成本价是120元,试销阶段,每件产品的销售价格x(元)与产品的日销售量y(件)之间的关系如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}x(元)
130
150
165
y(件)
70
50
35
(1)则y与x的函数关系式为__________;
y=-x+200
若销售量y是销售价格x的一次函数.
解:设销售利润为W元,则W=(x-120)y=(x-120)(-x+200)
=-x2+320x-24000=-(x-160)2+1600,∵-1<0,∴当x=160时,W取最大值,最大值为1600.
答:每件产品的销售价格定为160元时,此时每日的销售利润最大,最大利润是1600元.
当堂检测
(2)若要获得最大的销售利润,每件产品的销售价格定为多少元?此时每日的销售利润是多少?
当堂检测
8.王大伯决定销售一批风筝,经市场调研:蝙蝠形风筝每个进价为10元,当每个售价为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)求蝙蝠形风筝销售量y(个)与每个售价x(元)之间的函数表达式(12≤x≤30);
解:根据题意,得y=180-10(x-12)=-10x+300(12≤x≤30).
当堂检测
(2)当每个风筝的售价定为多少时,王大伯获得的利润最大,最大利润是多少?
解:设王大伯获得的利润为W元,则
W=(x-10)y=-10x2+400x-3000=-10(x-20)2+1000,∵-10<0,∴当x=20时,W取最大值,最大值为1000.
答:当每个风筝的售价定为20元时,王大伯获得的利润最大,最大利润是1000元.
当堂检测
9. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,经市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数表达式,并写出自变量x的取值范围;
x(元/件)
y(件)
10
16
24
30
O
解:(1)设y与x之间的函数关系式为y=kx+b,把(10,30),(16,24)代入,得????????????+????=????????,????????????+????=????????,
解得????=-????????=????????.∴y与x之间的函数表达式为y=-x+40(10≤x≤16).
?
当堂检测
(2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出当销售价为多少元/件时,每天的销售利润最大,最大利润是多少.
解:(2)W=(x-10)(-x+40)=-x2+50x-400(10≤x≤16).
∵W=-x2+50x-400=-(x-25)2+225,
函数图像的对称轴是直线x=25,在对称轴的左侧,y随着x的增大而增大.∵10≤x≤16,∴当x=16时,W最大,为144.即当销售价为16元/件时,每天的销售利润最大,最大利润是144元.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
