25.2 用列举法求概率 课件(共27张PPT)
文档属性
| 名称 | 25.2 用列举法求概率 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 00:00:00 | ||
图片预览








文档简介
人教版数学九年级上册
第25.2 用列举法求概率
学习目标
1.用列举法(包括列表、画树状图)计算简单事件发生的概率.
2.会用直接列举法、列表法和画树状图法列举所有可能出现的结果.
3.能够运用列表法和树状图法计算简单事件发生的概率.
4.会用列表法和画树状图法列举所有可能出现的结果.
老师向空中抛掷两枚同样的一元硬币,如果落地后一正一反,老师赢;如果落地后两面一样,你们赢.请问,你们觉得这个游戏公平吗?
情境引入
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正、正反、反正、反反.
所有可能的结果共有4种,并且这4种结果出现的可能性相等.
典例精析
(1)所有可能的结果中,满足两枚硬币全部正面向上(记为事件A)的结果只有一种,即“正正”,所以
P(A)=
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
典例精析
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
典例精析
(2)满足两枚硬币全部反面向上(记为事件B)的结果也只有1种,即“反反”,所以
P(B)=
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
典例精析
(3)一枚硬币正面向上,一枚硬币反面向上(记为事件C)的结果共有2种,即“反正”“正反”,所以
P(C)=
典例精析
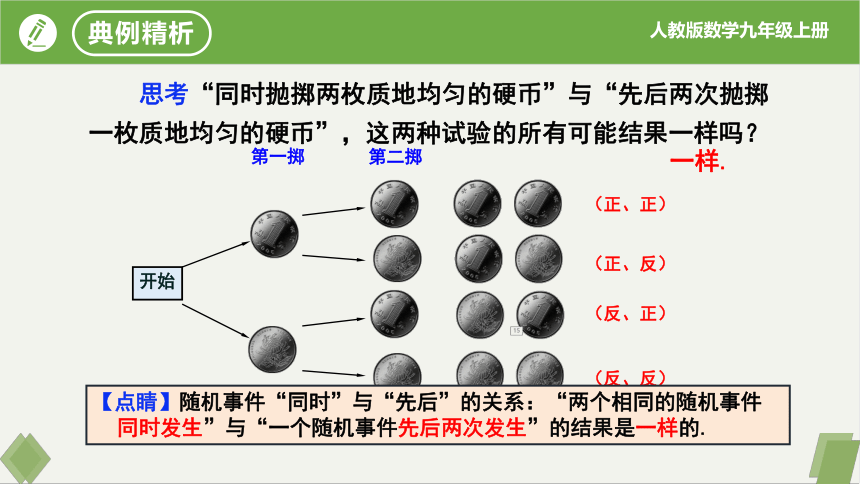
思考“同时抛掷两枚质地均匀的硬币”与“先后两次抛掷一枚质地均匀的硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
(正、正)
(正、反)
(反、正)
(反、反)
【点睛】随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
一样.
典例精析
例2 同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是9;
(3)至少有一枚骰子的点数为2.
分析:当一次试验要涉及两个因素(掷两枚骰子),并且可能出现的结果数目较多时,为了不重不漏地列出所有可能的结果,通常采用列表法.
典例精析
解:两枚骰子分别记为第一枚和第二枚,可以用下表列举出所有可能出现的结果.
由上表可以看出,同时掷两枚骰子,可能出现的结果有36种,并且它们出现的可能性相等.
典例精析
(1)两枚骰子的点数相同(记为事件A)的结果有6种(表中的红色部分),即(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),所以P(A)=
典例精析
(2)两枚骰子的点数和是9(记为事件B)的结果有4种(表中的阴影部分),即(3,6),(4,5),(5,4),(6,3),所以P(B)=
典例精析
(3)至少有一枚骰子的点数为2(记为事件C)的结果有11种(表中的蓝色部分),所以P(C)=
思考 如果把例2中的“同时掷两枚质地均匀的骰子”改为“把一枚质地均匀的骰子掷两次”,得到的结果有变化吗?为什么?
典例精析
一样.
【点睛】随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
例3 甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I. 从三个口袋中各随机地取出1个小球.
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少? ?
分析:当一次试验要涉及3个或更多的因素(从3个口袋中取球)时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
典例精析
解:根据题意,可以画出如下的树状图:
甲
乙
丙
A
B
E
C
D
E
C
D
I
H
I
H
I
H
I
H
I
H
I
H
典例精析
由树状图可以看出,所有可能出现的结果共有12种,即
这些结果出现的可能性相等.
典例精析
解:(1)只有1个元音字母的结果有5种,所以P(1个元音)= .
有2个元音字母的结果有4种,所以P(2个元音)=
全部为元音字母的结果只有1种,所以P(3个元音)= .
(2)全是辅音字母的结果有2种,所以P(3个辅音)= .
典例精析
1.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项那么两人同时选择“参加社会调查”的概率为( )
A.???????? B.???????? C.???????? D.????????
2.有A,B两个不透明的口袋,每个口袋里装有两个相同的球,A袋中的两个球上分别写了“细”、“致”的字样,B袋中的两个球上分别写了“信”、“心”的字样,从每个口袋里各摸出一个球,刚好能组成“细心”字样的概率是( )
A.???????? B.???????? C.???????? D.????????
?
A
B
小试牛刀
2.某人有红、白、蓝三件衬衫和红、白、蓝三条长裤,该人任意拿一件衬衫和一条长裤,正好是一套白色的概率___.
1.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
A. B. C. D.
D
课堂检测
3.在一个布袋里放有1个白球和2个红球,它们除颜色外其余都相同,从布袋里摸出1个球,记下颜色后放回,搅匀再摸出1个球.将2个红球分别记为红I,红ⅡI,两次摸球的所有可能的结果如表所示,则两次摸出的球都是红球的概率是_______.
课堂检测
1.在-2,-1,0,1,2这五个数中任取两数m,n,则抛物线y=(x-m)2+n的顶点在坐标轴上的概率为( )
A.???????? B.???????? C.???????? D.????????
2.将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为( )
A.???????? B.???????? C.???????? D.????????
?
B
D
拓展训练
3.甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少?
解:(1)画树状图得:
∴一共有12种等可能的结果,其中,取出的3个小球的标号全是奇数的有2种.
∴取出的3个小球的标号全是奇数的概率是:P= .
拓展训练
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
解:(2)∵这些线段能构成三角形的有:[2、4、3],[7、4、8],[7、4、9],[7、5、3],[7、5、8],[7、5、9]共6种.
这些线段能构成三角形的概率是:P= .
拓展训练
列举法
关键
常用
方法
直接列举法
画树状图法
在于正确列举出试验结果的各种可能性.
列表法
课堂小结
1.李老师为缓解小如和小意的压力,准备了四个完全相同(不透明)的锦囊,里面各装有一张纸条,分别写有:A.转移注意力,B.合理宣泄,C.自我暗示,D.放松训练.
(1)若小如随机取走一个锦囊,则取走的锦囊内纸条写有“C.自我暗示”的概率是 ;?
(2)若小如和小意两人先后随机抽取一个锦囊(抽取后不放回),请用列表或画树状图的方法求小如和小意都没有取走“B.合理宣泄”的概率.
课后作业
谢谢聆听
第25.2 用列举法求概率
学习目标
1.用列举法(包括列表、画树状图)计算简单事件发生的概率.
2.会用直接列举法、列表法和画树状图法列举所有可能出现的结果.
3.能够运用列表法和树状图法计算简单事件发生的概率.
4.会用列表法和画树状图法列举所有可能出现的结果.
老师向空中抛掷两枚同样的一元硬币,如果落地后一正一反,老师赢;如果落地后两面一样,你们赢.请问,你们觉得这个游戏公平吗?
情境引入
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正、正反、反正、反反.
所有可能的结果共有4种,并且这4种结果出现的可能性相等.
典例精析
(1)所有可能的结果中,满足两枚硬币全部正面向上(记为事件A)的结果只有一种,即“正正”,所以
P(A)=
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
典例精析
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
典例精析
(2)满足两枚硬币全部反面向上(记为事件B)的结果也只有1种,即“反反”,所以
P(B)=
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
典例精析
(3)一枚硬币正面向上,一枚硬币反面向上(记为事件C)的结果共有2种,即“反正”“正反”,所以
P(C)=
典例精析
思考“同时抛掷两枚质地均匀的硬币”与“先后两次抛掷一枚质地均匀的硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
(正、正)
(正、反)
(反、正)
(反、反)
【点睛】随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
一样.
典例精析
例2 同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是9;
(3)至少有一枚骰子的点数为2.
分析:当一次试验要涉及两个因素(掷两枚骰子),并且可能出现的结果数目较多时,为了不重不漏地列出所有可能的结果,通常采用列表法.
典例精析
解:两枚骰子分别记为第一枚和第二枚,可以用下表列举出所有可能出现的结果.
由上表可以看出,同时掷两枚骰子,可能出现的结果有36种,并且它们出现的可能性相等.
典例精析
(1)两枚骰子的点数相同(记为事件A)的结果有6种(表中的红色部分),即(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),所以P(A)=
典例精析
(2)两枚骰子的点数和是9(记为事件B)的结果有4种(表中的阴影部分),即(3,6),(4,5),(5,4),(6,3),所以P(B)=
典例精析
(3)至少有一枚骰子的点数为2(记为事件C)的结果有11种(表中的蓝色部分),所以P(C)=
思考 如果把例2中的“同时掷两枚质地均匀的骰子”改为“把一枚质地均匀的骰子掷两次”,得到的结果有变化吗?为什么?
典例精析
一样.
【点睛】随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
例3 甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I. 从三个口袋中各随机地取出1个小球.
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少? ?
分析:当一次试验要涉及3个或更多的因素(从3个口袋中取球)时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
典例精析
解:根据题意,可以画出如下的树状图:
甲
乙
丙
A
B
E
C
D
E
C
D
I
H
I
H
I
H
I
H
I
H
I
H
典例精析
由树状图可以看出,所有可能出现的结果共有12种,即
这些结果出现的可能性相等.
典例精析
解:(1)只有1个元音字母的结果有5种,所以P(1个元音)= .
有2个元音字母的结果有4种,所以P(2个元音)=
全部为元音字母的结果只有1种,所以P(3个元音)= .
(2)全是辅音字母的结果有2种,所以P(3个辅音)= .
典例精析
1.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项那么两人同时选择“参加社会调查”的概率为( )
A.???????? B.???????? C.???????? D.????????
2.有A,B两个不透明的口袋,每个口袋里装有两个相同的球,A袋中的两个球上分别写了“细”、“致”的字样,B袋中的两个球上分别写了“信”、“心”的字样,从每个口袋里各摸出一个球,刚好能组成“细心”字样的概率是( )
A.???????? B.???????? C.???????? D.????????
?
A
B
小试牛刀
2.某人有红、白、蓝三件衬衫和红、白、蓝三条长裤,该人任意拿一件衬衫和一条长裤,正好是一套白色的概率___.
1.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
A. B. C. D.
D
课堂检测
3.在一个布袋里放有1个白球和2个红球,它们除颜色外其余都相同,从布袋里摸出1个球,记下颜色后放回,搅匀再摸出1个球.将2个红球分别记为红I,红ⅡI,两次摸球的所有可能的结果如表所示,则两次摸出的球都是红球的概率是_______.
课堂检测
1.在-2,-1,0,1,2这五个数中任取两数m,n,则抛物线y=(x-m)2+n的顶点在坐标轴上的概率为( )
A.???????? B.???????? C.???????? D.????????
2.将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为( )
A.???????? B.???????? C.???????? D.????????
?
B
D
拓展训练
3.甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少?
解:(1)画树状图得:
∴一共有12种等可能的结果,其中,取出的3个小球的标号全是奇数的有2种.
∴取出的3个小球的标号全是奇数的概率是:P= .
拓展训练
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
解:(2)∵这些线段能构成三角形的有:[2、4、3],[7、4、8],[7、4、9],[7、5、3],[7、5、8],[7、5、9]共6种.
这些线段能构成三角形的概率是:P= .
拓展训练
列举法
关键
常用
方法
直接列举法
画树状图法
在于正确列举出试验结果的各种可能性.
列表法
课堂小结
1.李老师为缓解小如和小意的压力,准备了四个完全相同(不透明)的锦囊,里面各装有一张纸条,分别写有:A.转移注意力,B.合理宣泄,C.自我暗示,D.放松训练.
(1)若小如随机取走一个锦囊,则取走的锦囊内纸条写有“C.自我暗示”的概率是 ;?
(2)若小如和小意两人先后随机抽取一个锦囊(抽取后不放回),请用列表或画树状图的方法求小如和小意都没有取走“B.合理宣泄”的概率.
课后作业
谢谢聆听
同课章节目录
