27.1 图形的相似 课件(共22张PPT)
文档属性
| 名称 | 27.1 图形的相似 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 00:00:00 | ||
图片预览





文档简介
人教版数学九年级下册
第27.1 图形的相似
学习目标
1.了解相似图形和相似多边形的概念.
2.会根据条件判断两个多边形是否为相似多边形.
3.掌握相似多边形的性质,能根据相似比进行相关的计算.
全等图形
指能够完全重合的两个图形,即它们的形状和大小完全相同.
回忆
复习引入
互动新授
相同点:形状相同
不同点:大小不同
下面的每组图形有什么相同和不同的地方?
互动新授
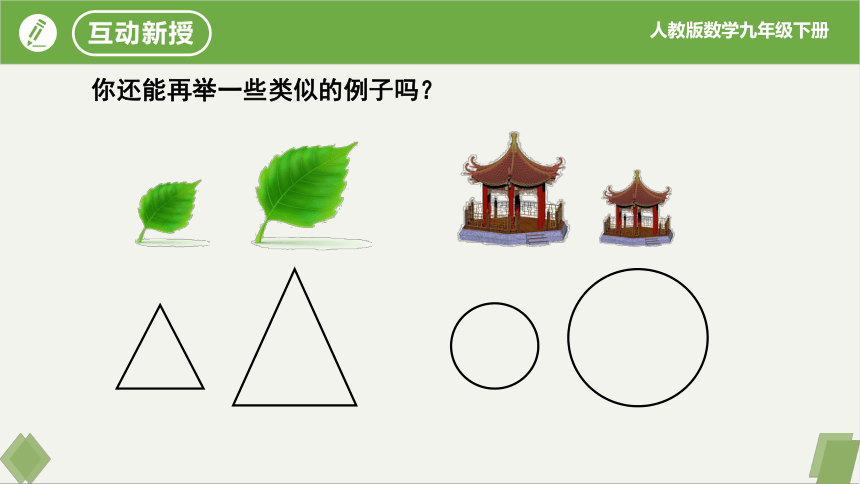
你还能再举一些类似的例子吗?
互动新授
你能给具有上述特点的图形起个名字吗?
定义:
我们把形状相同的图形叫做_________.
相似图形
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.例如,放映电影时,投在屏幕上的画面就是胶片上的图形的放大;用复印机把一个图形放大或缩小所得的图形,也都与原来的图形相似.其中较大(小)的图形可以看成是由较小(大)的图形放大(缩小)得到的.
互动新授
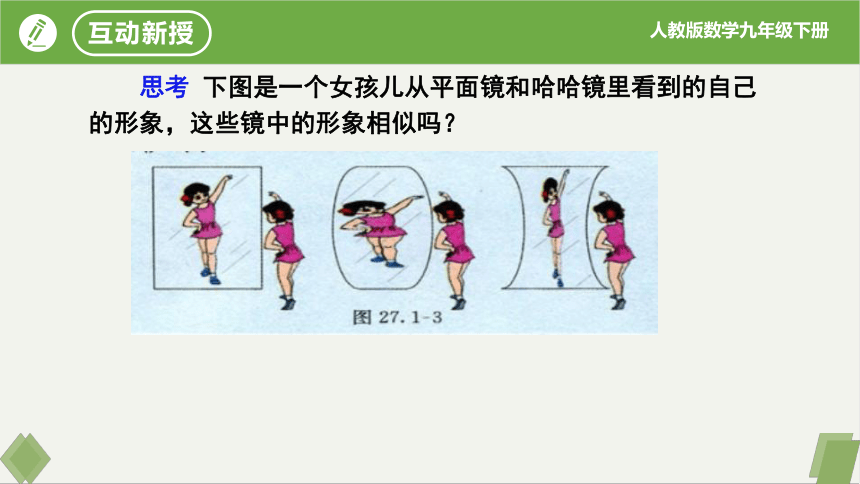
思考 下图是一个女孩儿从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象相似吗?
互动新授
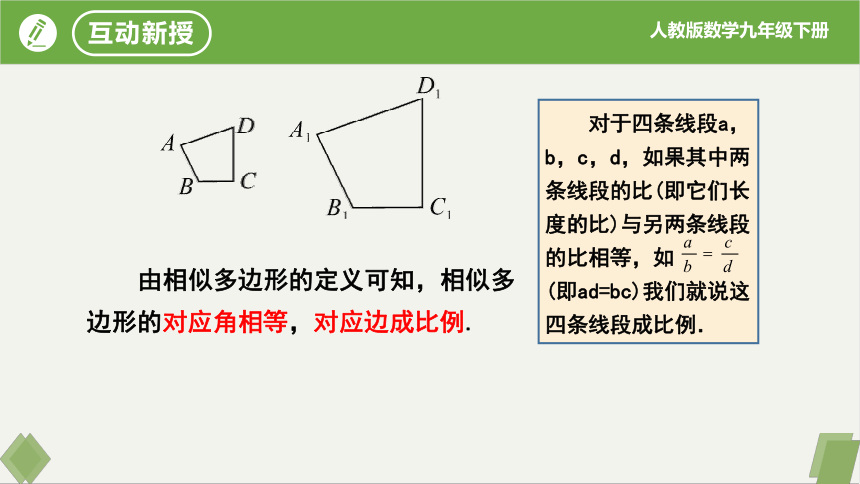
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
图中的两个大小不同的
四边形ABCD和四边形A1B1C1D1中,
∠A=∠A1,∠B=∠B1,∠C=∠C1,
∠D=∠D1,
,因此四边形ABCD与四边形A1B1C1D1相似.
互动新授
由相似多边形的定义可知,相似多边形的对应角相等,对应边成比例.
对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即ad=bc)我们就说这四条线段成比例.
典例精析
例 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
解:因为四边形ABCD和EFGH相似,所以它们的对应角相等.
由此可得α=∠C=83°,∠A=∠E=118°.
在四边形ABCD中,β=360°﹣(78°+83°+118°)=81°.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
典例精析
例 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
因为四边形ABCD和EFGH相似,所以它们的对应边成比例,
由此可得
解得 x=28.
1.下列四组长度的线段中,是成比例线段的是(?? )
A.4cm,5cm,6cm,7cm B.3cm,4cm,5cm,8cm
C.5cm,15cm,3cm,9cm D.8cm,4cm,1cm,3cm
C
小试牛刀
2.已知3、4、5、x成比例,则x的值为(??? ?)
A.???????????? B.???????????? C.???????????? D.6
3.若线段a,b,c,d是成比例线段,且????=????????????,????=????????????,????=????????????,则d=(?? ?)
A.8cm B.0.5cm C.2cm D.3cm
?
C
A
小试牛刀
1.如图所示的两个四边形相似,则α的度数是( )
A.60° B.75° C.87° D.120°
2. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为18,则这个多边形的最短边长为( )
A.6 B.8 C.12 D.10
3. 一个四边形的边长分别是4,5,6,7,另一个与它形状相同的四边形最短边长为8,则另一个四边形的周长是_____.
44
C
A
课堂检测
解:△ABC 为等边三角形.理由如下:
∵a,b,c 是△ABC 的三边长,∴a+b+c ≠0.
∵
∴
∴a=b=c. ∴△ABC 为等边三角形.
4.设a,b,c 是△ABC 的三边长,且
判断△ABC 为何种三角形,并说明理由.
课堂检测
1.如图,在△ABC 中,AB=24,AE=6,EC=10,
(1)求AD 的长;
(2)试说明
拓展训练
解:(1)设AD=x,则BD=24-x,
由 得 ,
解得x=9. ∴AD=9.
(2)由AB=24,AD=9得BD=15,
∵
∴
拓展训练
1.概念
2.相似比
3.性质
相似多边形
图形的相似
相似图形的概念
成比例线段
线段的比
四条线段成比例
课堂小结
1.如图所示的两个五边形相似,求a,b,c,d 的值.
解:a=3,b=4.5,c=4,d=6.
c
d
2
5
3
6
9
a
7.5
b
课后作业
2.如图,四边形ABCD 与四边形EFGH 相似,∠A=62°,∠B=70°,∠H=140°,AD=18,EF=15,FG=14,EH=12,求∠G 的度数及AB,BC 的长.
课后作业
解:∵四边形ABCD 与四边形EFGH 相似,
∴∠E=∠A=62°,∠F=∠B=70°,
∵∠H=140°,∠E+∠F+∠G+∠H=360°,
∴∠G=88°.
∵四边形ABCD 与四边形EFGH 相似,
∴ .
∵AD=18,EF=15,FG=14,EH=12,
∴AB=22.5,BC=21.
课后作业
谢谢聆听
第27.1 图形的相似
学习目标
1.了解相似图形和相似多边形的概念.
2.会根据条件判断两个多边形是否为相似多边形.
3.掌握相似多边形的性质,能根据相似比进行相关的计算.
全等图形
指能够完全重合的两个图形,即它们的形状和大小完全相同.
回忆
复习引入
互动新授
相同点:形状相同
不同点:大小不同
下面的每组图形有什么相同和不同的地方?
互动新授
你还能再举一些类似的例子吗?
互动新授
你能给具有上述特点的图形起个名字吗?
定义:
我们把形状相同的图形叫做_________.
相似图形
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.例如,放映电影时,投在屏幕上的画面就是胶片上的图形的放大;用复印机把一个图形放大或缩小所得的图形,也都与原来的图形相似.其中较大(小)的图形可以看成是由较小(大)的图形放大(缩小)得到的.
互动新授
思考 下图是一个女孩儿从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象相似吗?
互动新授
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
图中的两个大小不同的
四边形ABCD和四边形A1B1C1D1中,
∠A=∠A1,∠B=∠B1,∠C=∠C1,
∠D=∠D1,
,因此四边形ABCD与四边形A1B1C1D1相似.
互动新授
由相似多边形的定义可知,相似多边形的对应角相等,对应边成比例.
对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即ad=bc)我们就说这四条线段成比例.
典例精析
例 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
解:因为四边形ABCD和EFGH相似,所以它们的对应角相等.
由此可得α=∠C=83°,∠A=∠E=118°.
在四边形ABCD中,β=360°﹣(78°+83°+118°)=81°.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
典例精析
例 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
因为四边形ABCD和EFGH相似,所以它们的对应边成比例,
由此可得
解得 x=28.
1.下列四组长度的线段中,是成比例线段的是(?? )
A.4cm,5cm,6cm,7cm B.3cm,4cm,5cm,8cm
C.5cm,15cm,3cm,9cm D.8cm,4cm,1cm,3cm
C
小试牛刀
2.已知3、4、5、x成比例,则x的值为(??? ?)
A.???????????? B.???????????? C.???????????? D.6
3.若线段a,b,c,d是成比例线段,且????=????????????,????=????????????,????=????????????,则d=(?? ?)
A.8cm B.0.5cm C.2cm D.3cm
?
C
A
小试牛刀
1.如图所示的两个四边形相似,则α的度数是( )
A.60° B.75° C.87° D.120°
2. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为18,则这个多边形的最短边长为( )
A.6 B.8 C.12 D.10
3. 一个四边形的边长分别是4,5,6,7,另一个与它形状相同的四边形最短边长为8,则另一个四边形的周长是_____.
44
C
A
课堂检测
解:△ABC 为等边三角形.理由如下:
∵a,b,c 是△ABC 的三边长,∴a+b+c ≠0.
∵
∴
∴a=b=c. ∴△ABC 为等边三角形.
4.设a,b,c 是△ABC 的三边长,且
判断△ABC 为何种三角形,并说明理由.
课堂检测
1.如图,在△ABC 中,AB=24,AE=6,EC=10,
(1)求AD 的长;
(2)试说明
拓展训练
解:(1)设AD=x,则BD=24-x,
由 得 ,
解得x=9. ∴AD=9.
(2)由AB=24,AD=9得BD=15,
∵
∴
拓展训练
1.概念
2.相似比
3.性质
相似多边形
图形的相似
相似图形的概念
成比例线段
线段的比
四条线段成比例
课堂小结
1.如图所示的两个五边形相似,求a,b,c,d 的值.
解:a=3,b=4.5,c=4,d=6.
c
d
2
5
3
6
9
a
7.5
b
课后作业
2.如图,四边形ABCD 与四边形EFGH 相似,∠A=62°,∠B=70°,∠H=140°,AD=18,EF=15,FG=14,EH=12,求∠G 的度数及AB,BC 的长.
课后作业
解:∵四边形ABCD 与四边形EFGH 相似,
∴∠E=∠A=62°,∠F=∠B=70°,
∵∠H=140°,∠E+∠F+∠G+∠H=360°,
∴∠G=88°.
∵四边形ABCD 与四边形EFGH 相似,
∴ .
∵AD=18,EF=15,FG=14,EH=12,
∴AB=22.5,BC=21.
课后作业
谢谢聆听
