14.2.2 完全平方公式课件(共28张PPT)
文档属性
| 名称 | 14.2.2 完全平方公式课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 38.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 05:37:14 | ||
图片预览









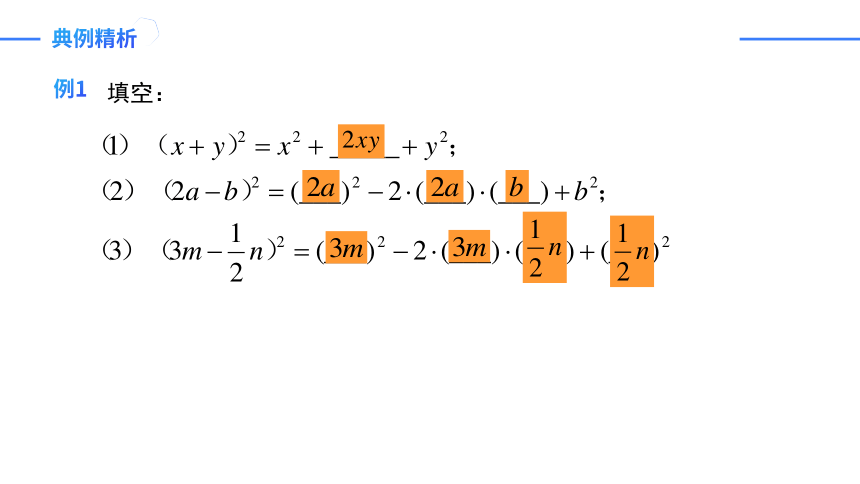
文档简介
(共30张PPT)
第14章
整式的乘法
与因式分解
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
14.2.2
完全平方公式
情景引入
小华去市场买一种水果,价格为每公斤9.8元,现称出该水果为9.8斤,小华随即报出了要付现金96.04元.你知道小华为什么算得怎么快吗?
新知探究
思考:
计算下列多项式的积,你能发现什么规律?
( p + 1 )2 = ( p + 1 )( p + 1 ) = p 2+2p+ 1
( m-2 )2 = ( m-2 )( m-2) = m2 -4m+4
新知探究
思考:
根据上面的规律,你能直接写出下列式子的运算结果吗?
(a+b)2 = .
a2 + 2ab + b2
(a-b)2 = .
a2-2ab + b2
法一:用多项式乘法证明:
(a-b)2
=(a-b)(a-b)
(a+b)2
=a2-ab-ab+b2
=a2-2ab+b2
=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
新知探究
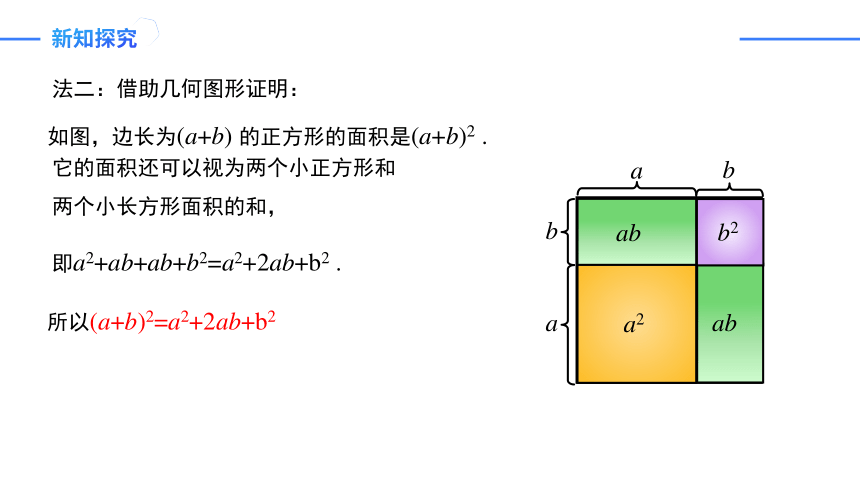
法二:借助几何图形证明:
如图,边长为(a+b) 的正方形的面积是(a+b)2 .
它的面积还可以视为两个小正方形和两个小长方形面积的和,
所以(a+b)2=a2+2ab+b2
b
a
a
b
a2
ab
ab
b2
即a2+ab+ab+b2=a2+2ab+b2 .
新知探究
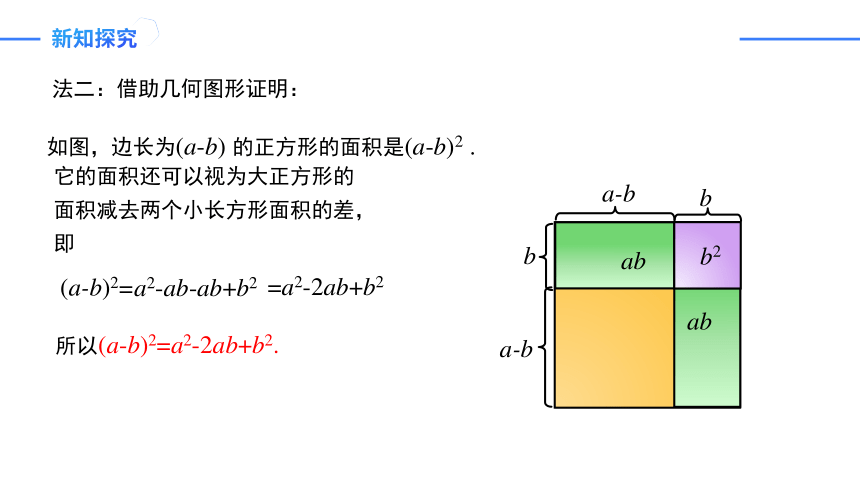
法二:借助几何图形证明:
它的面积还可以视为大正方形的面积减去两个小长方形面积的差,即
如图,边长为(a-b) 的正方形的面积是(a-b)2 .
所以(a-b)2=a2-2ab+b2.
(a-b)2
(a-b2)
a-b
b
b
a-b
ab
ab
b2
=a2-ab-ab+b2
=a2-2ab+b2
新知探究
(a+b)2=a2+2ab+b2,
我们把
(a-b)2=a2-2ab+b2.
都叫做完全平方公式.
文字语言:两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的 2 倍. 这两个公式叫做(乘法的)完全平方公式.
符号语言:
“首平方,尾平方,
积的 2 倍放中央.”
新知探究
思考:
观察下面两个完全平方式,比一比,回答下列问题:
1. 说一说积的次数和项数;
2. 两个完全平方式的积有相同的项吗?与 a,b 有什么关系?
3. 两个完全平方式的积中不同的是哪一项?与 a,b 有什么关系?它的符号与什么有关?
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2.
公式中的字母 a,b 可以表示数,单项式和多项式.
积为二次三项式;
积中两项为两数的平方和;
另一项是两数积的 2 倍,且与两数中间的符号相同;
新知探究
思考:
你能利用完全平方公式快速地计算出(2x+y)2吗?
可以这样算!
把2x与y分别看成上式的a与b,也就是把它们按下面的方法对应起来,就可以直接得到结果.
( 2x + y )2
( + )2
a
b
= ( )2 + · ( )· + 2
2x
2
2x
y
y
= 4x2+4xy+y2,
= a 2 + 2 · a · b + b 2 .
(a+b)2=a2+2ab+b2.
新知探究
思考:
下面各式的计算是否正确?如果不正确,应当怎样改正?
(1) (x + y)2 = x2 + y2
(2) (x-y)2 = x2-y2
(3) (-x + y)2 = x2 + 2xy + y2
(4) (2x + y)2 = 4x2 + 2xy + y2
×
×
×
×
x2 + 2xy + y2
x2-2xy + y2
x2-2xy + y2
4x2 + 4xy + y2
结果为二次三项式
结果为二次三项式
中间项符号错误
中间项系数错误
典例精析
例1
填空:
典例精析
例2
(1)(3m+n)2
解:(3m+n)2
= (3m)2+2 · 3m · n + n2
= 9m2+6mn+n2.
运用完全平方公式计算:
(a ± b)2 = a2 ± 2ab + b2
典例精析
例3
运用完全平方公式计算:
(1)(-x+1)2
解: (-x+1)2
= (-x)2+2(-x)· 1 + 12
= x2-2x+1
(2)(x-1)2
解: (x-1)2
= (x)2-2·x· 1 + 12
= x2-2x+1
对比
你有什么发现?
结论1:(a-b)2=(b-a)2.
解释: (b-a)2 = [-(a-b)]2=(a-b)2.
典例精析
例3
运用完全平方公式计算:
对比
你有什么发现?
结论2:(a+b)2=(-a-b)2.
解释: (-a-b)2= [-(a+b)]2=(a+b)2.
(3) (-2x-3)2
解 (-2x-3)2
= (-2x)2+2·(-2x)·(-3)+9
= 4x2+12x+9.
(4) (2x+3)2
解:原式=
= 4x2+12x+9.
典例精析
例4
(1) 2022;
解: 2022
= (200 + 2)2
= 40000 + 800 + 4
= 40804.
(2) 9.82.
解:9.82
= (10 – 0.2)2
= 100 - 4 + 0.04
= 96.04.
运用完全平方公式计算:
运用完全平方公式进行简便计算,要熟记完全平方公式的特征,将原式转化为能利用完全平方公式的形式.
典例精析
例5
利用乘法公式计算:
(1) 20232-2022×2024;
(2) 20232-2023×4042+20222.
=(2023-2022)2=1.
解:(1) 原式=20232-(2023+1)(2023-1)
=20232-20232+1=1.
(2) 原式=20232-2×2022×2023+20222
典例精析
例6
已知 x-y=6,xy=-8. 求:
(1) x2+y2 的值; (2) (x+y)2 的值.
=36-16=20.
解:(1) ∵ x-y=6,xy=-8,
(x-y)2=x2+y2-2xy,
∴ x2+y2=(x-y)2+2xy
(2) ∵ x2+y2=20,xy=-8,
∴ (x+y)2=x2+y2+2xy
=20-16=4.
典例精析
例7
图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形。
图(2)
图(1)
2a
2b
(1)图(2)中阴影部分的正方形的边长是_______;
(2)请用两种不同的方法求图(2)中阴影部分的面积:
方法一:__________;方法二:_______________.
(3)观察图(2),你能写出下列三个代数式之间的等量关系吗?
(4)根据第(3)题中的等量关系解决如下问题:
若 , ,则 =_______。
28
新知探究
思考:
从例6和例7中,你能得到什么启发?
完全平方公式的常见变形
去括号与添括号
新知探究
a + (b + c) = a + b + c;
a – (b + c) = a – b – c.
a + b + c = a + (b + c);
a – b – c = a – (b + c).
去括号:
把上面两个等式的左右两边反过来,
就得到添括号法则:
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
去括号与添括号
新知探究
将等号左右两边对换,等式仍然成立.
a+b+c=a+(b+c)
a b c=a (b+c)
符号不变
符号不变
添上“+( )”,括号里的各项都不变符号.
符号改变
符号改变
添上“ ( )”,括号里的各项都改变符号.
典例精析
例8
计算:(1) (a-b+c)2;
(2) (1-2m+n)(1+2m-n).
=1-4m2+4mn-n2.
解:(1) 原式=[(a-b)+c]2
=(a-b)2+c2+2(a-b)c
=a2-2ab+b2+c2+2ac-2bc.
(2) 原式=[1-(2m-n)][1+(2m-n)]
=12-(2m-n)2
归纳总结
完全平方公式
法则
注意
(a±b)2 = a2±2ab + b2
1. 项数、符号、字母及其指数
2. 不能直接应用公式进行计算的
式子,可能需要先添括号,变
形成符合公式的形式才行
常用
结论
3. 弄清完全平方公式和平方差公
式的不同(从公式结构特点及
结果两方面)
a2+b2 = (a+b)2-2ab = (a-b)2+2ab;
4ab = (a + b)2 - (a - b)2.
当堂检测
1.计算:(2x-y)2=( )
A. 4x2-4xy+y2
B. 4x2-2xy+y2
C. 4x2-y2
D. 4x2+y2
(2x)2 -2·2x·y+y2
4x2 -4xy+y2
A
2.将1052变形正确的是( )
A. 1052=1002+52 B.1052=(100-5)(100+5)
C. 1052=1002+2×100×5+52 D.1052=1002+100×5+52
C
当堂检测
3.若(3x-a)2=9x2-bx+16,则a+b的值为( )
A.28 B.-28 C.24或-24 D.28或-28
D
解:因为(3x-a)2=9x2-6ax+a2,
所以9x2-6ax+a2=9x2-bx+16.
则a2=16,6a=b,
解得a=±4.
当a=4时,b=24;当a=-4时,b=-24.
所以a+b=28或-28.
4.
已知(m+n+1)(m+n 1)=63,则m+n= .
解:∵ (m+n+1)(m+n 1)=(m+n)2 12=63
∴(m+n)2=64 ∴m+n= 8
8
当堂检测
5.利用完全平方公式计算:
(1) (5-a)2; (2) (-3m-4n)2; (3) (-3a+b)2.
(3) (-3a+b)2=9a2-6ab+b2.
解:(1) (5-a)2=25-10a+a2.
(2) (-3m-4n)2=9m2+24mn+16n2.
(4) (-4a+5b)2 =(5b-4a)2 =(5b)2-2·5b·4a+(4a)2=25b2-40ab+16a2 ;
(5) (x+7y)2 =x2+2·x·7y+(7y)2=x2+14xy+49y2 .
(4) (-4a+5b)2 ; (5) (x+7y)2 .
当堂检测
6.利用完全平方公式计算:
(1)5012; (2)2992;
(3)1992-202×198; (4)472-94×27+272.
解:(1)原式=(500+1)2=5002+2×500×1+12=251 001.
(2)原式=(300-1)2=3002-2×300×1+12=89 401.
(3)原式=(200-1)2-(200+2)(200-2)
=2002-2×200×1+12-(2002-22)= -395.
(4)原式=(47-27)2= 400.
当堂检测
7.运用乘法公式计算:
(1) (x + 2y - 3)(x - 2y + 3); (2) (a + b + c)2.
原式 = [x + (2y – 3)][x – (2y – 3)]
解:(1)
(2) 原式 = [(a + b) + c]2
= x2 – (2y – 3)2
= x2 – (4y2 – 12y + 9)
= x2 – 4y2 + 12y – 9.
= (a + b)2 + 2(a + b)c + c2
= a2 + 2ab + b2 + 2ac + 2bc + c2.
当堂检测
8.已知m+n=8,mn=6,求m2+n2,(m-n)2 .
分析:先将m2+n2,(m-n)2变形为用m+n, mn表示的式子,然后将已知整体代入求值.
解:因为m+n=8,mn=6,
所以m2+n2=(m+n)2-2mn=82-2×6=52,
m2-n2=(m+n)2-4mn=82-4×6=40.
第14章
整式的乘法
与因式分解
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
14.2.2
完全平方公式
情景引入
小华去市场买一种水果,价格为每公斤9.8元,现称出该水果为9.8斤,小华随即报出了要付现金96.04元.你知道小华为什么算得怎么快吗?
新知探究
思考:
计算下列多项式的积,你能发现什么规律?
( p + 1 )2 = ( p + 1 )( p + 1 ) = p 2+2p+ 1
( m-2 )2 = ( m-2 )( m-2) = m2 -4m+4
新知探究
思考:
根据上面的规律,你能直接写出下列式子的运算结果吗?
(a+b)2 = .
a2 + 2ab + b2
(a-b)2 = .
a2-2ab + b2
法一:用多项式乘法证明:
(a-b)2
=(a-b)(a-b)
(a+b)2
=a2-ab-ab+b2
=a2-2ab+b2
=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
新知探究
法二:借助几何图形证明:
如图,边长为(a+b) 的正方形的面积是(a+b)2 .
它的面积还可以视为两个小正方形和两个小长方形面积的和,
所以(a+b)2=a2+2ab+b2
b
a
a
b
a2
ab
ab
b2
即a2+ab+ab+b2=a2+2ab+b2 .
新知探究
法二:借助几何图形证明:
它的面积还可以视为大正方形的面积减去两个小长方形面积的差,即
如图,边长为(a-b) 的正方形的面积是(a-b)2 .
所以(a-b)2=a2-2ab+b2.
(a-b)2
(a-b2)
a-b
b
b
a-b
ab
ab
b2
=a2-ab-ab+b2
=a2-2ab+b2
新知探究
(a+b)2=a2+2ab+b2,
我们把
(a-b)2=a2-2ab+b2.
都叫做完全平方公式.
文字语言:两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的 2 倍. 这两个公式叫做(乘法的)完全平方公式.
符号语言:
“首平方,尾平方,
积的 2 倍放中央.”
新知探究
思考:
观察下面两个完全平方式,比一比,回答下列问题:
1. 说一说积的次数和项数;
2. 两个完全平方式的积有相同的项吗?与 a,b 有什么关系?
3. 两个完全平方式的积中不同的是哪一项?与 a,b 有什么关系?它的符号与什么有关?
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2.
公式中的字母 a,b 可以表示数,单项式和多项式.
积为二次三项式;
积中两项为两数的平方和;
另一项是两数积的 2 倍,且与两数中间的符号相同;
新知探究
思考:
你能利用完全平方公式快速地计算出(2x+y)2吗?
可以这样算!
把2x与y分别看成上式的a与b,也就是把它们按下面的方法对应起来,就可以直接得到结果.
( 2x + y )2
( + )2
a
b
= ( )2 + · ( )· + 2
2x
2
2x
y
y
= 4x2+4xy+y2,
= a 2 + 2 · a · b + b 2 .
(a+b)2=a2+2ab+b2.
新知探究
思考:
下面各式的计算是否正确?如果不正确,应当怎样改正?
(1) (x + y)2 = x2 + y2
(2) (x-y)2 = x2-y2
(3) (-x + y)2 = x2 + 2xy + y2
(4) (2x + y)2 = 4x2 + 2xy + y2
×
×
×
×
x2 + 2xy + y2
x2-2xy + y2
x2-2xy + y2
4x2 + 4xy + y2
结果为二次三项式
结果为二次三项式
中间项符号错误
中间项系数错误
典例精析
例1
填空:
典例精析
例2
(1)(3m+n)2
解:(3m+n)2
= (3m)2+2 · 3m · n + n2
= 9m2+6mn+n2.
运用完全平方公式计算:
(a ± b)2 = a2 ± 2ab + b2
典例精析
例3
运用完全平方公式计算:
(1)(-x+1)2
解: (-x+1)2
= (-x)2+2(-x)· 1 + 12
= x2-2x+1
(2)(x-1)2
解: (x-1)2
= (x)2-2·x· 1 + 12
= x2-2x+1
对比
你有什么发现?
结论1:(a-b)2=(b-a)2.
解释: (b-a)2 = [-(a-b)]2=(a-b)2.
典例精析
例3
运用完全平方公式计算:
对比
你有什么发现?
结论2:(a+b)2=(-a-b)2.
解释: (-a-b)2= [-(a+b)]2=(a+b)2.
(3) (-2x-3)2
解 (-2x-3)2
= (-2x)2+2·(-2x)·(-3)+9
= 4x2+12x+9.
(4) (2x+3)2
解:原式=
= 4x2+12x+9.
典例精析
例4
(1) 2022;
解: 2022
= (200 + 2)2
= 40000 + 800 + 4
= 40804.
(2) 9.82.
解:9.82
= (10 – 0.2)2
= 100 - 4 + 0.04
= 96.04.
运用完全平方公式计算:
运用完全平方公式进行简便计算,要熟记完全平方公式的特征,将原式转化为能利用完全平方公式的形式.
典例精析
例5
利用乘法公式计算:
(1) 20232-2022×2024;
(2) 20232-2023×4042+20222.
=(2023-2022)2=1.
解:(1) 原式=20232-(2023+1)(2023-1)
=20232-20232+1=1.
(2) 原式=20232-2×2022×2023+20222
典例精析
例6
已知 x-y=6,xy=-8. 求:
(1) x2+y2 的值; (2) (x+y)2 的值.
=36-16=20.
解:(1) ∵ x-y=6,xy=-8,
(x-y)2=x2+y2-2xy,
∴ x2+y2=(x-y)2+2xy
(2) ∵ x2+y2=20,xy=-8,
∴ (x+y)2=x2+y2+2xy
=20-16=4.
典例精析
例7
图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形。
图(2)
图(1)
2a
2b
(1)图(2)中阴影部分的正方形的边长是_______;
(2)请用两种不同的方法求图(2)中阴影部分的面积:
方法一:__________;方法二:_______________.
(3)观察图(2),你能写出下列三个代数式之间的等量关系吗?
(4)根据第(3)题中的等量关系解决如下问题:
若 , ,则 =_______。
28
新知探究
思考:
从例6和例7中,你能得到什么启发?
完全平方公式的常见变形
去括号与添括号
新知探究
a + (b + c) = a + b + c;
a – (b + c) = a – b – c.
a + b + c = a + (b + c);
a – b – c = a – (b + c).
去括号:
把上面两个等式的左右两边反过来,
就得到添括号法则:
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
去括号与添括号
新知探究
将等号左右两边对换,等式仍然成立.
a+b+c=a+(b+c)
a b c=a (b+c)
符号不变
符号不变
添上“+( )”,括号里的各项都不变符号.
符号改变
符号改变
添上“ ( )”,括号里的各项都改变符号.
典例精析
例8
计算:(1) (a-b+c)2;
(2) (1-2m+n)(1+2m-n).
=1-4m2+4mn-n2.
解:(1) 原式=[(a-b)+c]2
=(a-b)2+c2+2(a-b)c
=a2-2ab+b2+c2+2ac-2bc.
(2) 原式=[1-(2m-n)][1+(2m-n)]
=12-(2m-n)2
归纳总结
完全平方公式
法则
注意
(a±b)2 = a2±2ab + b2
1. 项数、符号、字母及其指数
2. 不能直接应用公式进行计算的
式子,可能需要先添括号,变
形成符合公式的形式才行
常用
结论
3. 弄清完全平方公式和平方差公
式的不同(从公式结构特点及
结果两方面)
a2+b2 = (a+b)2-2ab = (a-b)2+2ab;
4ab = (a + b)2 - (a - b)2.
当堂检测
1.计算:(2x-y)2=( )
A. 4x2-4xy+y2
B. 4x2-2xy+y2
C. 4x2-y2
D. 4x2+y2
(2x)2 -2·2x·y+y2
4x2 -4xy+y2
A
2.将1052变形正确的是( )
A. 1052=1002+52 B.1052=(100-5)(100+5)
C. 1052=1002+2×100×5+52 D.1052=1002+100×5+52
C
当堂检测
3.若(3x-a)2=9x2-bx+16,则a+b的值为( )
A.28 B.-28 C.24或-24 D.28或-28
D
解:因为(3x-a)2=9x2-6ax+a2,
所以9x2-6ax+a2=9x2-bx+16.
则a2=16,6a=b,
解得a=±4.
当a=4时,b=24;当a=-4时,b=-24.
所以a+b=28或-28.
4.
已知(m+n+1)(m+n 1)=63,则m+n= .
解:∵ (m+n+1)(m+n 1)=(m+n)2 12=63
∴(m+n)2=64 ∴m+n= 8
8
当堂检测
5.利用完全平方公式计算:
(1) (5-a)2; (2) (-3m-4n)2; (3) (-3a+b)2.
(3) (-3a+b)2=9a2-6ab+b2.
解:(1) (5-a)2=25-10a+a2.
(2) (-3m-4n)2=9m2+24mn+16n2.
(4) (-4a+5b)2 =(5b-4a)2 =(5b)2-2·5b·4a+(4a)2=25b2-40ab+16a2 ;
(5) (x+7y)2 =x2+2·x·7y+(7y)2=x2+14xy+49y2 .
(4) (-4a+5b)2 ; (5) (x+7y)2 .
当堂检测
6.利用完全平方公式计算:
(1)5012; (2)2992;
(3)1992-202×198; (4)472-94×27+272.
解:(1)原式=(500+1)2=5002+2×500×1+12=251 001.
(2)原式=(300-1)2=3002-2×300×1+12=89 401.
(3)原式=(200-1)2-(200+2)(200-2)
=2002-2×200×1+12-(2002-22)= -395.
(4)原式=(47-27)2= 400.
当堂检测
7.运用乘法公式计算:
(1) (x + 2y - 3)(x - 2y + 3); (2) (a + b + c)2.
原式 = [x + (2y – 3)][x – (2y – 3)]
解:(1)
(2) 原式 = [(a + b) + c]2
= x2 – (2y – 3)2
= x2 – (4y2 – 12y + 9)
= x2 – 4y2 + 12y – 9.
= (a + b)2 + 2(a + b)c + c2
= a2 + 2ab + b2 + 2ac + 2bc + c2.
当堂检测
8.已知m+n=8,mn=6,求m2+n2,(m-n)2 .
分析:先将m2+n2,(m-n)2变形为用m+n, mn表示的式子,然后将已知整体代入求值.
解:因为m+n=8,mn=6,
所以m2+n2=(m+n)2-2mn=82-2×6=52,
m2-n2=(m+n)2-4mn=82-4×6=40.
