14.3.1 提公因式法 课件(共28张PPT)
文档属性
| 名称 | 14.3.1 提公因式法 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 05:36:20 | ||
图片预览






文档简介
第14章
整式的乘法
与因式分解
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
14.3.1
提公因式法
情景引入
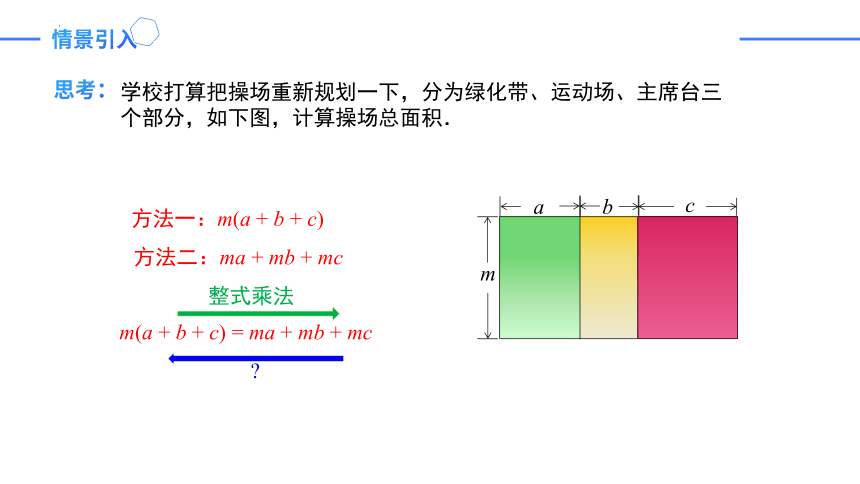
学校打算把操场重新规划一下,分为绿化带、运动场、主席台三个部分,如下图,计算操场总面积.
a
b
c
m
方法一:m(a + b + c)
方法二:ma + mb + mc
m(a + b + c) = ma + mb + mc
整式乘法
?
思考:
情景引入
思考:
算一算
你是用什么方法计算的?这个式子的各项有相同的因数吗?
解:
新知探究
思考:
1. 运用整式乘法法则或公式填空:
(1) p(a + b + c) = ;
(2) (y + 1)(y - 1) = ;
(3) (a + b)2 = .
pa + pb + pc
y2 - 1
a2 + 2ab + b2
2. 根据等式的性质填空:
(1) pa + pb + pc = ( )( );
(2) y2 - 1 = ( )( );
(3) a2 + 2ab + b2 = ( )2.
p a + b + c
y + 1 x - 1
a + b
都是多项式化为几个整式的积的形式
比一比,这些式子有什么共同点?
新知探究
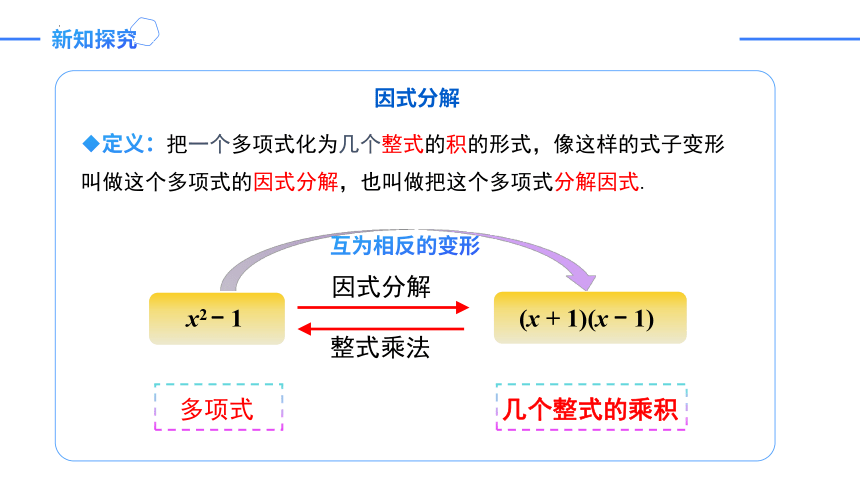
因式分解
定义:把一个多项式化为几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式.
x2 - 1 (x + 1)(x - 1)
因式分解
整式乘法
互为相反的变形
多项式
几个整式的乘积
新知探究
思考:
x2 + x = x2(1 + )
在下列等式中,从左到右的变形属于因式分解的有 ;
不是因式分解的,请说明为什么.
①
②
③
④
⑤
⑥
③
⑥
ax + bx + c = x(a + b) + c
12x2y = 3x·4xy
p2- 1 = (p + 1)(p- 1)
(2m + 1)2 = 4m2 + 4m + 1
2a + 4b + 6c = 2(a + 2b + 3c)
最后不是积的形式
因式分解的对象是多项式
是整式乘法
每个因式必须是整式
是因式分解
是因式分解
提公因式
新知探究
思考:
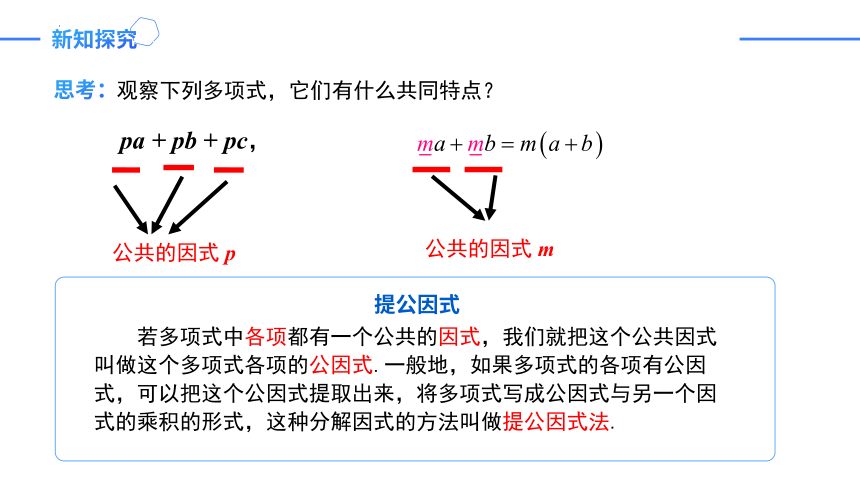
pa + pb + pc,
若多项式中各项都有一个公共的因式,我们就把这个公共因式叫做这个多项式各项的公因式.一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
公共的因式 p
观察下列多项式,它们有什么共同特点?
公共的因式 m
新知探究
思考:
1) ac+ bc
2)3 x2 +9xy
3) a2b – 2ab2 + ab
4) 4xy2-6xy+8x3y
(1)下列各多项式中的公因式是什么?
c
3x
ab
2xy
(2)多项式中的公因式是如何确定的?
讨论:
新知探究
确定一个多项式的公因式的方法
01
02
03
提公因式
相同字母的指数取各项中最小的一个,即字母最低次幂
定指数
字母取多项式各项中都含有的相同的字母.
定字母
公因式的系数是多项式各项系数的最大公约数.
定系数
新知探究
思考:
指出下列各多项式中各项的公因式:
{EB9631B5-78F2-41C9-869B-9F39066F8104}多项式
公因式
典例精析
例1
把下列各式因式分解:
解:
典例精析
例2
把下列各式因式分解.
解:
公因式既可以是一个单项式的形式,也可以是一个多项式的形式
典例精析
提公因式法步骤
即将多项式化为两个因式的乘积.
是数学中一种重要而且常用的思想方法
找出公因式
提公因式
整体思想
典例精析
例3
把下列各式因式分解:
解:
(y-x)=-(x-y)
(n-m)2=(m-n)2
典例精析
例4
下面是小明同学的错题本,请你帮他订正.
{2D5ABB26-0587-4C30-8999-92F81FD0307C}日期:
原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析
□审题不清
□计算错误
□时间不足
□概念不清
□其他原因
原因及分析:
因式分解:12x2y + 18xy2.
解:原式 = 3xy(4x + 6y).
注意:公因式要提尽.
正确解:原式 = 6xy(2x + 3y).
典例精析
例4
下面是小明同学的错题本,请你帮他订正.
{2D5ABB26-0587-4C30-8999-92F81FD0307C}日期:
原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析
□审题不清
□计算错误
□时间不足
□概念不清
□其他原因
原因及分析:
解:原式 = x(3x - 6y).
因式分解:3x2 - 6xy + x.
注意:某项提出莫漏 1.
正确解:原式 = 3x·x - 6y·x + 1·x
= x(3x - 6y + 1)
典例精析
例4
下面是小明同学的错题本,请你帮他订正.
{2D5ABB26-0587-4C30-8999-92F81FD0307C}日期:
原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析
□审题不清
□计算错误
□时间不足
□概念不清
□其他原因
原因及分析:
因式分解:- x2 + xy - xz.
解:原式 = - x(x + y - z).
注意:首项有负常提负.
正确解:原式 = - (x2 - xy + xz)
= - x(x - y + z).
典例精析
归纳总结
①提取不尽
③疏忽变号
④只提取部分公因式,整个式子未成乘积形式.
(3)提取公因式的一般步骤:
①确定应提取的公因式:
②用公因式去除这个多项式,把所得的商作为另一个因式:
③把多项式写成这两个因式的积的形式.
(2)提取公因式要彻底;注意易犯的错误:
②漏项
(1)当首项系数为负时,通常应提取负因数,在提取“-”号时,余下的各项都变号.
归纳总结
典例精析
例5
计算:
(1) 39×37-13×91;
(2) 29×20.23+72×20.23+13×20.23-20.23×14.
(2) 原式=20.23×(29+72+13-14) = 2023.
=13×20=260.
解:(1) 原式=3×13×37-13×91
=13×(3×37-91)
在计算求值时,若式子各项都含有公因式,用提取公因式的方法可使运算简便.
归纳总结
典例精析
例6
已知 a+b=7,ab=4,求 a2b+ab2 的值.
∴ a2b+ab2=ab(a+b)=4×7=28.
解:∵ a+b=7,ab=4,
含 a±b,ab 的求值题,通常要将所求式子进行因式分解,变形为能用 a±b 和 ab 表示的式子,然后将 a±b,ab 的值整体代入求解.
归纳总结
因式
分解
定义
am + bm + mc = m(a + b + c)
提公因式法
确定公因式的方法:三定,即定系数;定字母;定指数
分两步:第一步找公因式;第二步提公因式
注意:①分解因式是一种恒等变形;②公因式:要提尽;③不要漏项;④提负号,要注意变号
归纳总结
各项有公先提公,
首项有负常提负,
某项提出莫漏一,
括号里面分到底.
当堂检测
D
2.分解-4x3+8x2+16x的结果是( )
(A)-x(4x2-8x+16) (B)x(-4x2+8x-16)
(C)4(-x3+2x2-4x) (D)-4x(x2-2x-4)
1.多项式-6ab2+18a2b2-12a3b2c的公因式是( )
(A)-6ab2c (B)-ab2 (C)-6ab2 (D)-6a3b2C
C
3.下列用提公因式法分解因式正确的是( )
(A)12abc-9a2b2=3abc(4-3ab)
(B)3x2y-3xy+6y=3y(x2-x+2y)
(C)-a2+ab-ac=-a(a-b+c)
(D)x2y+5xy-y=y(x2+5x)
C
当堂检测
4.若多项式-6ab+18abx+24aby的一个因式是-6ab, 那么另一个因式是( )
(A)-1-3x+4y (B)1+3x-4y
(C)-1-3x-4y (D)1-3x-4y
D
5.下列多项式中,不能用提公因式法因式分解的是( )
A. ????3?????+1 B. (?????????)?4(?????????)2
C. 11????2?????7????2 D.5????????+?????3????2(????+????)
?
A
6.把多项式3(?????????)2+2(?????????)3分解因式结果正确的是( )
A.?????????2(3?2?????2????) B.?????????2(3?2????+2????)
C.?????????2(3+2?????2????) D.?????????2(3+2?????2????)
?
B
当堂检测
7.因式分解:(?????????)2+????(?????????).
?
解法1:(?????????)2+????(?????????)
=(?????????)2?????(?????????)
=(?????????)(??????????????)
=(?????????)(?????2????).
?
解法2:(?????????)2+????(?????????)
=(?????????)2+????(???????)
=(?????????)(?????????+????)
=(?????????)(2?????????).
?
8.已知2????+????=3,5?????3????=?2,
求代数式2????+????2?????3????+3????(2????+????)的值.
?
解: 2????+????2?????3????+3????(2????+????)=2????+????2?????3????+3????
=2????+????5?????3????,
∵ 2????+????=3,5?????3????=?2, ∴原式=?6.
?
当堂检测
9.把下列各式分解因式:
(1)2x3+6x2
(2)3pq3+15p3q
(3)4x2-8ax+2x
(4)-3ab+6abx-9aby
解 : 原式= 2x2(x+3)
解 : 原式= 3pq(q2+5p2 )
解 : 原式=2x(2x-4a+1)
解 : 原式=-3ab(1-2x+3y)
当堂检测
阅读下列因式分解的过程,再回答所提出的问题:
1+????+????????+1+????(????+1)2
=(1+????)1+????+????(????+1)
=1+????21+????
=(1+????)3
(1)上述分解因式的方法是 ,共应用了 次;
?
提公因式法
2
(2)若分解1+????+????????+1+????(????+1)2+…+????(????+1)2023,则需应用上述
方法 次;
(3)分解因式:
1+????+????????+1+????(????+1)2+…+????(????+1)????= (????为正整数).
?
2023
(????+1)????+1
整式的乘法
与因式分解
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
14.3.1
提公因式法
情景引入
学校打算把操场重新规划一下,分为绿化带、运动场、主席台三个部分,如下图,计算操场总面积.
a
b
c
m
方法一:m(a + b + c)
方法二:ma + mb + mc
m(a + b + c) = ma + mb + mc
整式乘法
?
思考:
情景引入
思考:
算一算
你是用什么方法计算的?这个式子的各项有相同的因数吗?
解:
新知探究
思考:
1. 运用整式乘法法则或公式填空:
(1) p(a + b + c) = ;
(2) (y + 1)(y - 1) = ;
(3) (a + b)2 = .
pa + pb + pc
y2 - 1
a2 + 2ab + b2
2. 根据等式的性质填空:
(1) pa + pb + pc = ( )( );
(2) y2 - 1 = ( )( );
(3) a2 + 2ab + b2 = ( )2.
p a + b + c
y + 1 x - 1
a + b
都是多项式化为几个整式的积的形式
比一比,这些式子有什么共同点?
新知探究
因式分解
定义:把一个多项式化为几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式.
x2 - 1 (x + 1)(x - 1)
因式分解
整式乘法
互为相反的变形
多项式
几个整式的乘积
新知探究
思考:
x2 + x = x2(1 + )
在下列等式中,从左到右的变形属于因式分解的有 ;
不是因式分解的,请说明为什么.
①
②
③
④
⑤
⑥
③
⑥
ax + bx + c = x(a + b) + c
12x2y = 3x·4xy
p2- 1 = (p + 1)(p- 1)
(2m + 1)2 = 4m2 + 4m + 1
2a + 4b + 6c = 2(a + 2b + 3c)
最后不是积的形式
因式分解的对象是多项式
是整式乘法
每个因式必须是整式
是因式分解
是因式分解
提公因式
新知探究
思考:
pa + pb + pc,
若多项式中各项都有一个公共的因式,我们就把这个公共因式叫做这个多项式各项的公因式.一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
公共的因式 p
观察下列多项式,它们有什么共同特点?
公共的因式 m
新知探究
思考:
1) ac+ bc
2)3 x2 +9xy
3) a2b – 2ab2 + ab
4) 4xy2-6xy+8x3y
(1)下列各多项式中的公因式是什么?
c
3x
ab
2xy
(2)多项式中的公因式是如何确定的?
讨论:
新知探究
确定一个多项式的公因式的方法
01
02
03
提公因式
相同字母的指数取各项中最小的一个,即字母最低次幂
定指数
字母取多项式各项中都含有的相同的字母.
定字母
公因式的系数是多项式各项系数的最大公约数.
定系数
新知探究
思考:
指出下列各多项式中各项的公因式:
{EB9631B5-78F2-41C9-869B-9F39066F8104}多项式
公因式
典例精析
例1
把下列各式因式分解:
解:
典例精析
例2
把下列各式因式分解.
解:
公因式既可以是一个单项式的形式,也可以是一个多项式的形式
典例精析
提公因式法步骤
即将多项式化为两个因式的乘积.
是数学中一种重要而且常用的思想方法
找出公因式
提公因式
整体思想
典例精析
例3
把下列各式因式分解:
解:
(y-x)=-(x-y)
(n-m)2=(m-n)2
典例精析
例4
下面是小明同学的错题本,请你帮他订正.
{2D5ABB26-0587-4C30-8999-92F81FD0307C}日期:
原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析
□审题不清
□计算错误
□时间不足
□概念不清
□其他原因
原因及分析:
因式分解:12x2y + 18xy2.
解:原式 = 3xy(4x + 6y).
注意:公因式要提尽.
正确解:原式 = 6xy(2x + 3y).
典例精析
例4
下面是小明同学的错题本,请你帮他订正.
{2D5ABB26-0587-4C30-8999-92F81FD0307C}日期:
原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析
□审题不清
□计算错误
□时间不足
□概念不清
□其他原因
原因及分析:
解:原式 = x(3x - 6y).
因式分解:3x2 - 6xy + x.
注意:某项提出莫漏 1.
正确解:原式 = 3x·x - 6y·x + 1·x
= x(3x - 6y + 1)
典例精析
例4
下面是小明同学的错题本,请你帮他订正.
{2D5ABB26-0587-4C30-8999-92F81FD0307C}日期:
原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析
□审题不清
□计算错误
□时间不足
□概念不清
□其他原因
原因及分析:
因式分解:- x2 + xy - xz.
解:原式 = - x(x + y - z).
注意:首项有负常提负.
正确解:原式 = - (x2 - xy + xz)
= - x(x - y + z).
典例精析
归纳总结
①提取不尽
③疏忽变号
④只提取部分公因式,整个式子未成乘积形式.
(3)提取公因式的一般步骤:
①确定应提取的公因式:
②用公因式去除这个多项式,把所得的商作为另一个因式:
③把多项式写成这两个因式的积的形式.
(2)提取公因式要彻底;注意易犯的错误:
②漏项
(1)当首项系数为负时,通常应提取负因数,在提取“-”号时,余下的各项都变号.
归纳总结
典例精析
例5
计算:
(1) 39×37-13×91;
(2) 29×20.23+72×20.23+13×20.23-20.23×14.
(2) 原式=20.23×(29+72+13-14) = 2023.
=13×20=260.
解:(1) 原式=3×13×37-13×91
=13×(3×37-91)
在计算求值时,若式子各项都含有公因式,用提取公因式的方法可使运算简便.
归纳总结
典例精析
例6
已知 a+b=7,ab=4,求 a2b+ab2 的值.
∴ a2b+ab2=ab(a+b)=4×7=28.
解:∵ a+b=7,ab=4,
含 a±b,ab 的求值题,通常要将所求式子进行因式分解,变形为能用 a±b 和 ab 表示的式子,然后将 a±b,ab 的值整体代入求解.
归纳总结
因式
分解
定义
am + bm + mc = m(a + b + c)
提公因式法
确定公因式的方法:三定,即定系数;定字母;定指数
分两步:第一步找公因式;第二步提公因式
注意:①分解因式是一种恒等变形;②公因式:要提尽;③不要漏项;④提负号,要注意变号
归纳总结
各项有公先提公,
首项有负常提负,
某项提出莫漏一,
括号里面分到底.
当堂检测
D
2.分解-4x3+8x2+16x的结果是( )
(A)-x(4x2-8x+16) (B)x(-4x2+8x-16)
(C)4(-x3+2x2-4x) (D)-4x(x2-2x-4)
1.多项式-6ab2+18a2b2-12a3b2c的公因式是( )
(A)-6ab2c (B)-ab2 (C)-6ab2 (D)-6a3b2C
C
3.下列用提公因式法分解因式正确的是( )
(A)12abc-9a2b2=3abc(4-3ab)
(B)3x2y-3xy+6y=3y(x2-x+2y)
(C)-a2+ab-ac=-a(a-b+c)
(D)x2y+5xy-y=y(x2+5x)
C
当堂检测
4.若多项式-6ab+18abx+24aby的一个因式是-6ab, 那么另一个因式是( )
(A)-1-3x+4y (B)1+3x-4y
(C)-1-3x-4y (D)1-3x-4y
D
5.下列多项式中,不能用提公因式法因式分解的是( )
A. ????3?????+1 B. (?????????)?4(?????????)2
C. 11????2?????7????2 D.5????????+?????3????2(????+????)
?
A
6.把多项式3(?????????)2+2(?????????)3分解因式结果正确的是( )
A.?????????2(3?2?????2????) B.?????????2(3?2????+2????)
C.?????????2(3+2?????2????) D.?????????2(3+2?????2????)
?
B
当堂检测
7.因式分解:(?????????)2+????(?????????).
?
解法1:(?????????)2+????(?????????)
=(?????????)2?????(?????????)
=(?????????)(??????????????)
=(?????????)(?????2????).
?
解法2:(?????????)2+????(?????????)
=(?????????)2+????(???????)
=(?????????)(?????????+????)
=(?????????)(2?????????).
?
8.已知2????+????=3,5?????3????=?2,
求代数式2????+????2?????3????+3????(2????+????)的值.
?
解: 2????+????2?????3????+3????(2????+????)=2????+????2?????3????+3????
=2????+????5?????3????,
∵ 2????+????=3,5?????3????=?2, ∴原式=?6.
?
当堂检测
9.把下列各式分解因式:
(1)2x3+6x2
(2)3pq3+15p3q
(3)4x2-8ax+2x
(4)-3ab+6abx-9aby
解 : 原式= 2x2(x+3)
解 : 原式= 3pq(q2+5p2 )
解 : 原式=2x(2x-4a+1)
解 : 原式=-3ab(1-2x+3y)
当堂检测
阅读下列因式分解的过程,再回答所提出的问题:
1+????+????????+1+????(????+1)2
=(1+????)1+????+????(????+1)
=1+????21+????
=(1+????)3
(1)上述分解因式的方法是 ,共应用了 次;
?
提公因式法
2
(2)若分解1+????+????????+1+????(????+1)2+…+????(????+1)2023,则需应用上述
方法 次;
(3)分解因式:
1+????+????????+1+????(????+1)2+…+????(????+1)????= (????为正整数).
?
2023
(????+1)????+1
