14.2.1 平方差公式 课件(共29张PPT)
文档属性
| 名称 | 14.2.1 平方差公式 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 52.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 05:45:32 | ||
图片预览







文档简介
(共29张PPT)
第14章
整式的乘法
与因式分解
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
14.2.1
平方差公式
复习引入
新知探究
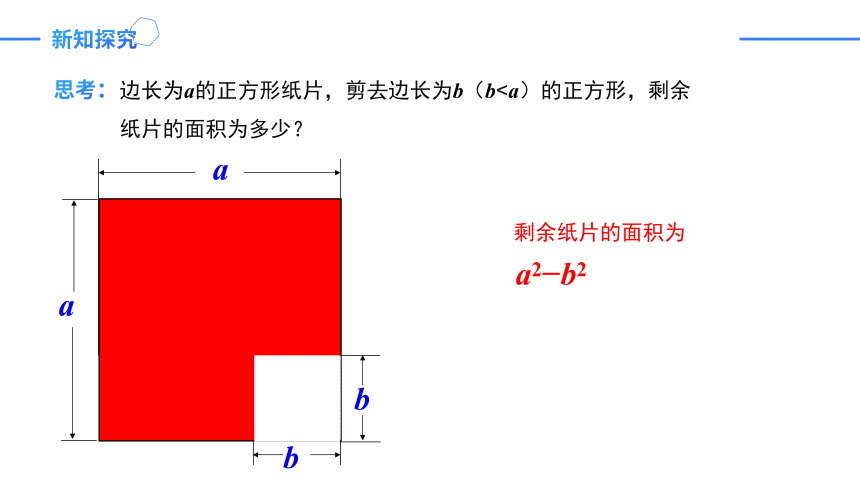
思考:
边长为a的正方形纸片,剪去边长为b(bb
a
a
b
a2 b2
剩余纸片的面积为
新知探究
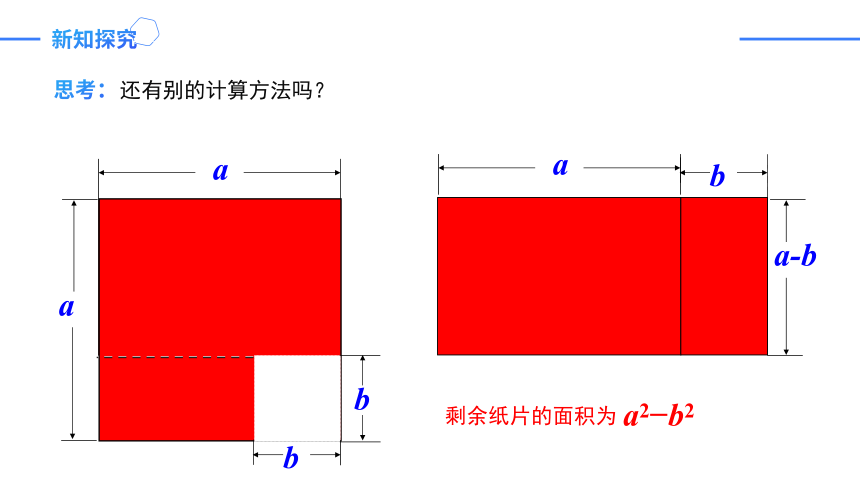
思考:
还有别的计算方法吗?
b
a
a
b
a
b
a-b
a2 b2
剩余纸片的面积为
新知探究
思考:
还有别的计算方法吗?
b
a
a
b
剩余纸片的面积为
b
a
a
b
1
2
(a+b)(a-b)
1
2
(a+b)(a-b)
(a+b)(a-b)
新知探究
平方差公式
(a + b)(a b) =
a2 b2.
两数和与这两数差的积,等于这两数的平方差.
公式变形:
1. (a – b)(a + b) = a2 – b2;
2. (b + a)(–b + a) = a2 – b2.
由于剩余纸片面积相等,于是有:
新知探究
平方差公式解读
平方差公式
注意:这里的两数可以是两个单项式,也可以是两个
多项式等.
(a + b)(a - b) = a2 - b2
相同为 a
相反为 b
顺序可以不同,只关注相同的符号
可以合理加括号,只关注相反的符号
新知探究
思考:
判断下列式子是否可用平方差公式?
(1)(-a+b)(a+b) (2) (-a+b)(a-b)
(3)(a+b)(a-c) (4)(2+a)(a-2)
(5)
(6) (1-x)(-x-1)
(7) (-4k3+3y2)(-4k3-3y2)
符号都是相反
字母不对应
新知探究
积累:
常见的平方差公式及其变形
(l) (-a + b)(a + b) =_________.
(2) (a-b)(b + a) = _________.
(3) (-a-b)(-a + b) = ________.
(4) (a-b)(-a-b) = _________.
a2-b2
a2-b2
b2-a2
b2-a2
关注字母(或多项式)的符号
与顺序无关!
常见的公式和变形要熟记!
典例精析
例1
下面各式的计算对不对?如果不对,应当怎样改正?
(1) ;
(2) ;
(3) ;
(4) .
两个字母符号相同,
不能运用公式
公式运用错误
符号识别错误
新知探究
公式再熟悉:
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(0.3x)2-12
(a + b)(a - b)
(1 + x)(1 - x)
(-3 + a)(-3 - a)
(0.3x - 1)(1 + 0.3x)
(1 + a)(-1 + a)
典例精析
例2
(1)(a+3b)(a– 3b);
=4a2–9;
=4x4–y2.
原式=(2a+3)(2a–3)
=a2–9b2 ;
=(2a)2–32
原式=(–2x2 )2–y2
原式=(a)2–(3b)2
(2)(3+2a)(–3+2a);
(3)(–2x2–y)(–2x2+y).
计算:
(4) (-7m+8n)(-8n-7m).
原式=(-7m)2-(8n)2
=49m2-64n2.
新知探究
应用平方差公式计算时,应注意以下几个问题:
(1) 左边是两个二项式相乘,并且这两个二项式中有一项完全相同,
另一项互为相反数;
(2) 右边是相同项的平方减去相反项的平方;
(3) 公式中的 a 和 b 可以是具体的数,也可以是单项式或多项式.
归纳总结
新知探究
①位置变化
②符号变化
③系数变化
④指数变化
⑤增因式变化
(x+y)(x-y)(-x-y)(-x+y)
=(x2-y2)(x2-y2)
⑥增项变化
⑦连用公式变化
(x+y)(x-y)(x2+y2)
=(x2-y2)(x2+y2)=x4-y4
典例精析
例3
运用平方差公式计算:
(1) (a+3b)(a - 3b);
(2) (3+2a)(- 3+2a);
(3) 51 × 49;
(4) (3x+4)(3x-4)-(2x+3)(2x-3).
(1) 原式=a2-9b2;
(2) 原式=4a2-9;
(3) 原式=(50+1)(50-1)=502-12=2499;
(4) 原式=(3x)2-42-[(2x)2-32]=5x2-7.
解:
典例精析
例4
计算:
(1)a2(a+b)(a-b)+a2b2; (2)(2x-5)(2x+5) –2x(2x-3) .
解:
(1)原式=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4;
(2)原式=(2x)2-25-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
典例精析
例5
解方程或不等式:
(1)(2x+1)(2x-1)+3(x+2)(x-2)=(7x+1)(x-1)
(2)求(x+5)(x+2)-(x+2)(x-2)<28的正整数解.
解:(1) 4x2-1+3(x2-4)=7x2-6x-1
4x2-1+3x2-12= 7x2-6x-1
6x=12
x=2
(2) x2+7x+10-x2+4 <28
7x +14<28
x <2 因为x为正整数,所以不等式的解取1.
典例精析
例6
王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
解:李大妈吃亏了.
理由如下:原正方形的面积为a2,
改变边长后面积为(a+4)(a-4)=a2-16.
∵a2>a2-16,
∴李大妈吃亏了.
典例精析
例7
若(a+b+1)(a+b-1)=63,则a+b=——
解:(a+b)2-1=63
(a+b)2=64
a+b=±8
整体法
典例精析
例8
先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中 x=1,y=2.
原式=5×12-5×22=-15.
解:原式=4x2-y2-(4y2-x2)
=4x2-y2-4y2+x2
=5x2-5y2.
当 x=1,y=2 时,
典例精析
例9
已知 x≠1,计算:
(1+x)(1-x)=1-x2,(1-x)(1+x+x2)=1-x3,
(1-x)(1+x+x2+x3)=1-x4……
(1) 观察以上各式并猜想:(1-x)(1+x+x2+…+xn)=________
( n 为正整数);
(2) 根据你的猜想计算:
① (1-2)(1+2+22+23+24+25)=______;
② 2+22+23+…+2n=__________ (n 为正整数);
③ (x-1)(x99+x98+x97+…+x2+x+1)=________;
1-xn+1
-63
2n+1-2
x100-1
(3) 通过以上规律请你进行下面的探索:
① (a-b)(a+b)=_______;
② (a-b)(a2+ab+b2)=________;
a2-b2
a3-b3
归纳总结
平方差公式
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.抓住 “一同一反”这一特征,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
内容
当堂检测
1. 计算(2x+1)(2x–1)等于( )
A.4x2–1 B.2x2–1 C.4x–1 D.4x2+1
A
2. 两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是________.
10
3.计算:118×122=________.
14396
4. 下列运算中,可用平方差公式计算的是 ( )
A.(x+y)(x+y) B.(-x+y)(x-y)
C.(-x-y)(y-x) D.(x+y)(-x-y)
C
当堂检测
6.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
5.(x-y)(x+y)(x2+y2);
解:原式=(x2-y2)(x2+y2)=x4-y4;
当堂检测
7. 利用平方差公式计算:
(1)(a-2)(a+2)(a2+4);
解:原式 = (a2-4)(a2+4)
= a4-16.
(2) (x-y)(x+y)(x2+y2)(x4+y4).
解:原式 = (x2-y2)(x2+y2)(x4+y4)
= (x4-y4)(x4+y4)
= x8-y8.
当堂检测
8.计算:
(1) 20232-2022×2024;
(2) (y+2) (y-2) – (y-1) (y+5) .
解:(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= -4y + 1.
解:
20232-2022×2024
= 20232-(2023-1)(2023 + 1)
= 20232
-(20232-12 )
= 20232-20232 + 12
= 1.
当堂检测
9.先化简,再求值:
(1)(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2;
解:原式=5x2-5y2.当x=1,y=2时,
原式=-15;
(2)-4x(x2-2x-1)+x(2x+5)(2x-5),其中x=-1.
解:原式=8x2-21x.当x=-1时,原式=29.
当堂检测
10.对于任意的正整数 n,整式 (3n+1)(3n-1)-(3-n)(3+n) 的值一定是 10 的整数倍吗?
即整式 (3n+1)(3n-1)-(3-n)(3+n) 的值一定是 10 的整数倍.
解:原式=9n2-1-(9-n2)
=10n2-10.
∵ (10n2-10)÷10=n2-1,
n 为正整数,
∴ n2-1 一定为整数.
第14章
整式的乘法
与因式分解
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
14.2.1
平方差公式
复习引入
新知探究
思考:
边长为a的正方形纸片,剪去边长为b(b
a
a
b
a2 b2
剩余纸片的面积为
新知探究
思考:
还有别的计算方法吗?
b
a
a
b
a
b
a-b
a2 b2
剩余纸片的面积为
新知探究
思考:
还有别的计算方法吗?
b
a
a
b
剩余纸片的面积为
b
a
a
b
1
2
(a+b)(a-b)
1
2
(a+b)(a-b)
(a+b)(a-b)
新知探究
平方差公式
(a + b)(a b) =
a2 b2.
两数和与这两数差的积,等于这两数的平方差.
公式变形:
1. (a – b)(a + b) = a2 – b2;
2. (b + a)(–b + a) = a2 – b2.
由于剩余纸片面积相等,于是有:
新知探究
平方差公式解读
平方差公式
注意:这里的两数可以是两个单项式,也可以是两个
多项式等.
(a + b)(a - b) = a2 - b2
相同为 a
相反为 b
顺序可以不同,只关注相同的符号
可以合理加括号,只关注相反的符号
新知探究
思考:
判断下列式子是否可用平方差公式?
(1)(-a+b)(a+b) (2) (-a+b)(a-b)
(3)(a+b)(a-c) (4)(2+a)(a-2)
(5)
(6) (1-x)(-x-1)
(7) (-4k3+3y2)(-4k3-3y2)
符号都是相反
字母不对应
新知探究
积累:
常见的平方差公式及其变形
(l) (-a + b)(a + b) =_________.
(2) (a-b)(b + a) = _________.
(3) (-a-b)(-a + b) = ________.
(4) (a-b)(-a-b) = _________.
a2-b2
a2-b2
b2-a2
b2-a2
关注字母(或多项式)的符号
与顺序无关!
常见的公式和变形要熟记!
典例精析
例1
下面各式的计算对不对?如果不对,应当怎样改正?
(1) ;
(2) ;
(3) ;
(4) .
两个字母符号相同,
不能运用公式
公式运用错误
符号识别错误
新知探究
公式再熟悉:
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(0.3x)2-12
(a + b)(a - b)
(1 + x)(1 - x)
(-3 + a)(-3 - a)
(0.3x - 1)(1 + 0.3x)
(1 + a)(-1 + a)
典例精析
例2
(1)(a+3b)(a– 3b);
=4a2–9;
=4x4–y2.
原式=(2a+3)(2a–3)
=a2–9b2 ;
=(2a)2–32
原式=(–2x2 )2–y2
原式=(a)2–(3b)2
(2)(3+2a)(–3+2a);
(3)(–2x2–y)(–2x2+y).
计算:
(4) (-7m+8n)(-8n-7m).
原式=(-7m)2-(8n)2
=49m2-64n2.
新知探究
应用平方差公式计算时,应注意以下几个问题:
(1) 左边是两个二项式相乘,并且这两个二项式中有一项完全相同,
另一项互为相反数;
(2) 右边是相同项的平方减去相反项的平方;
(3) 公式中的 a 和 b 可以是具体的数,也可以是单项式或多项式.
归纳总结
新知探究
①位置变化
②符号变化
③系数变化
④指数变化
⑤增因式变化
(x+y)(x-y)(-x-y)(-x+y)
=(x2-y2)(x2-y2)
⑥增项变化
⑦连用公式变化
(x+y)(x-y)(x2+y2)
=(x2-y2)(x2+y2)=x4-y4
典例精析
例3
运用平方差公式计算:
(1) (a+3b)(a - 3b);
(2) (3+2a)(- 3+2a);
(3) 51 × 49;
(4) (3x+4)(3x-4)-(2x+3)(2x-3).
(1) 原式=a2-9b2;
(2) 原式=4a2-9;
(3) 原式=(50+1)(50-1)=502-12=2499;
(4) 原式=(3x)2-42-[(2x)2-32]=5x2-7.
解:
典例精析
例4
计算:
(1)a2(a+b)(a-b)+a2b2; (2)(2x-5)(2x+5) –2x(2x-3) .
解:
(1)原式=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4;
(2)原式=(2x)2-25-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
典例精析
例5
解方程或不等式:
(1)(2x+1)(2x-1)+3(x+2)(x-2)=(7x+1)(x-1)
(2)求(x+5)(x+2)-(x+2)(x-2)<28的正整数解.
解:(1) 4x2-1+3(x2-4)=7x2-6x-1
4x2-1+3x2-12= 7x2-6x-1
6x=12
x=2
(2) x2+7x+10-x2+4 <28
7x +14<28
x <2 因为x为正整数,所以不等式的解取1.
典例精析
例6
王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
解:李大妈吃亏了.
理由如下:原正方形的面积为a2,
改变边长后面积为(a+4)(a-4)=a2-16.
∵a2>a2-16,
∴李大妈吃亏了.
典例精析
例7
若(a+b+1)(a+b-1)=63,则a+b=——
解:(a+b)2-1=63
(a+b)2=64
a+b=±8
整体法
典例精析
例8
先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中 x=1,y=2.
原式=5×12-5×22=-15.
解:原式=4x2-y2-(4y2-x2)
=4x2-y2-4y2+x2
=5x2-5y2.
当 x=1,y=2 时,
典例精析
例9
已知 x≠1,计算:
(1+x)(1-x)=1-x2,(1-x)(1+x+x2)=1-x3,
(1-x)(1+x+x2+x3)=1-x4……
(1) 观察以上各式并猜想:(1-x)(1+x+x2+…+xn)=________
( n 为正整数);
(2) 根据你的猜想计算:
① (1-2)(1+2+22+23+24+25)=______;
② 2+22+23+…+2n=__________ (n 为正整数);
③ (x-1)(x99+x98+x97+…+x2+x+1)=________;
1-xn+1
-63
2n+1-2
x100-1
(3) 通过以上规律请你进行下面的探索:
① (a-b)(a+b)=_______;
② (a-b)(a2+ab+b2)=________;
a2-b2
a3-b3
归纳总结
平方差公式
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.抓住 “一同一反”这一特征,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
内容
当堂检测
1. 计算(2x+1)(2x–1)等于( )
A.4x2–1 B.2x2–1 C.4x–1 D.4x2+1
A
2. 两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是________.
10
3.计算:118×122=________.
14396
4. 下列运算中,可用平方差公式计算的是 ( )
A.(x+y)(x+y) B.(-x+y)(x-y)
C.(-x-y)(y-x) D.(x+y)(-x-y)
C
当堂检测
6.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
5.(x-y)(x+y)(x2+y2);
解:原式=(x2-y2)(x2+y2)=x4-y4;
当堂检测
7. 利用平方差公式计算:
(1)(a-2)(a+2)(a2+4);
解:原式 = (a2-4)(a2+4)
= a4-16.
(2) (x-y)(x+y)(x2+y2)(x4+y4).
解:原式 = (x2-y2)(x2+y2)(x4+y4)
= (x4-y4)(x4+y4)
= x8-y8.
当堂检测
8.计算:
(1) 20232-2022×2024;
(2) (y+2) (y-2) – (y-1) (y+5) .
解:(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= -4y + 1.
解:
20232-2022×2024
= 20232-(2023-1)(2023 + 1)
= 20232
-(20232-12 )
= 20232-20232 + 12
= 1.
当堂检测
9.先化简,再求值:
(1)(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2;
解:原式=5x2-5y2.当x=1,y=2时,
原式=-15;
(2)-4x(x2-2x-1)+x(2x+5)(2x-5),其中x=-1.
解:原式=8x2-21x.当x=-1时,原式=29.
当堂检测
10.对于任意的正整数 n,整式 (3n+1)(3n-1)-(3-n)(3+n) 的值一定是 10 的整数倍吗?
即整式 (3n+1)(3n-1)-(3-n)(3+n) 的值一定是 10 的整数倍.
解:原式=9n2-1-(9-n2)
=10n2-10.
∵ (10n2-10)÷10=n2-1,
n 为正整数,
∴ n2-1 一定为整数.
