第19章 几何证明 单元复习课件 (共38张PPT)
文档属性
| 名称 | 第19章 几何证明 单元复习课件 (共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 05:22:44 | ||
图片预览










文档简介
沪教版八年级上册
第 19 章 几何证明
单元复习(4个概念2个性质3个判定2个定理2个应用2种思想方法1个轨迹)
学习目标
1.理解命题、逆命题、定理、逆定理等的含义;
2.掌握证明真命题正确性的方法步骤,会举反例说明假命题的错误;掌握证明线段相等 角度相等的基本方法和思路;
3.理解轨迹的定义,掌握三种基本轨迹;
4.能判断直角三角形全等,能应用勾股定理及其逆定理解决实际问题.
?
1.下列语句是命题吗?如果是,请将它们改写成“如果……,那么……”的形式.并指出条件和结论。
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
如果两条直线被第三条直线所截,那么同旁内角互补;
如果等式两边都加同一个数,那么结果仍是等式;
如果两个数互为相反数,那么这两个数相加得0;
如果两个角是同旁内角,那么这两个角互补;
4个概念
考点01 命题
考点02 互逆命题
1 [2022·上海中考]下列说法正确的是( A )
A.命题一定有逆命题
B.所有的定理一定有逆定理
C.真命题的逆命题一定是真命题
D.假命题的逆命题一定是假命题
A
解析:A.命题一定有逆命题,此选项说法正确;B.不是所有的定理一定有逆定理,如“全等三角形的对应角相等”没有逆定理,此选项说法错误;C.真命题的逆命题不一定是真命题,如“对顶角相等”的逆命题是假命题,此选项说法错误;D.假命题的逆命题不一定是假命题,如假命题“对应角相等的三角形全等”,其逆命题是真命题,此选项说法错误.故选A.
2 [2022·江苏无锡中考]请写出命题“如果a>b,那么b-a<0”的逆命题:? 如果b-a<0,那么a>b ?.?
如
果b-a<0,那么a>b
考点03 公理、定理
3. 下列真命题能作为公理的是 ( )
A.对顶角相等
B.三角形的内角和是180°
C.过一点有且只有一条直线与已知直线垂直
D.内错角相等,两直线平行
4.“经过两点有且只有一条直线”是( )
A.公理 B.假命题
C.定义 D.以上都不是
C
A
5.命题“直角三角形的两个锐角互余”是( )
A.角的定义 B.假命题
C.公理 D.定理
分析:可以用逻辑推理的方法判断此命题是正确的
D
定义、命题、公理、定理之间的区别与联系:
(1)联系:这四者都是命题.
(2)区别:定义、公理、定理都是真命题,都可以作为进一步判断其他命题真假的依据,只不过公理是最原始的依据;而命题不一定是真命题,因而不能作为进一步判断其他命题真假的依据.
考点04 互逆定理
6. [2022·江苏无锡宜兴市二模]下列命题的逆命题成立的是? ①④ ?.?
①同旁内角互补,两直线平行
②等边三角形是锐角三角形
③如果两个实数相等,那么它们的平方相等
①④
④全等三角形的三条边对应相等
解析:①“同旁内角互补,两直线平行”的逆命题为“两直线平行,同旁内角互补”,成立;②“等边三角形是锐角三角形”的逆命题为“锐角三角形是等边三角形”,不成立;③“如果两个实数相等,那么它们的平方相等”的逆命题为“平方相等的两个实数相等”,不成立;④“全等三角形的三条边对应相等”的逆命题为“三条边对应相等的三角形全等”,成立.故答案为①④.
7.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
考点05 线段的垂直平分线
2个性质3个判定
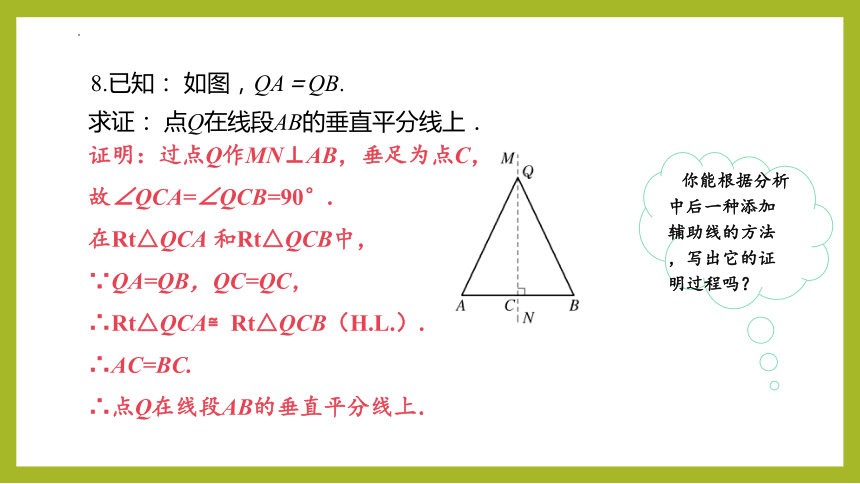
证明:过点Q作MN⊥AB,垂足为点C,
故∠QCA=∠QCB=90°.
在Rt△QCA 和Rt△QCB中,
∵QA=QB,QC=QC,
∴Rt△QCA≌Rt△QCB(H.L.).
∴AC=BC.
∴点Q在线段AB的垂直平分线上.
8.已知: 如图,QA=QB.
求证: 点Q在线段AB的垂直平分线上.
你能根据分析中后一种添加辅助线的方法,写出它的证明过程吗?
证明:∵OP为∠AOB的平分线,PC⊥OA,PD⊥OB,
∴PC=PD.
在Rt△OCP和Rt△ODP中,
∵ OP=OP,
PC=PD,
∴Rt△OCP≌ Rt△ODP(HL).
∴ ∠CPO=∠DPO,OC=OD.
9.如图,OP为∠AOB 的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D,则下列结论错误的是( )
A.PC=PD B.∠CPO=∠DOP C.∠CPO=∠DPO D.OC=OD
B
考点06 角平分线
分析:在△ABC中,∠C=90°, ∴DC⊥AC.
又∵DE⊥AB,AD平分∠CAB, ∴DC=DE.
在Rt△ACD和Rt△AED中, AD=AD,
DC=DE,
∴Rt△ACD≌Rt△AED(HL), ∴AC=AE.
∵AC=BC, ∴AE=BC, ∴△DEB的周长为8cm.
10.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,
DE⊥AB,垂足为E,若AB=8cm,则△DEB 的周长为( )
A.10cm B.7cm C.8cm D.不能确定
C
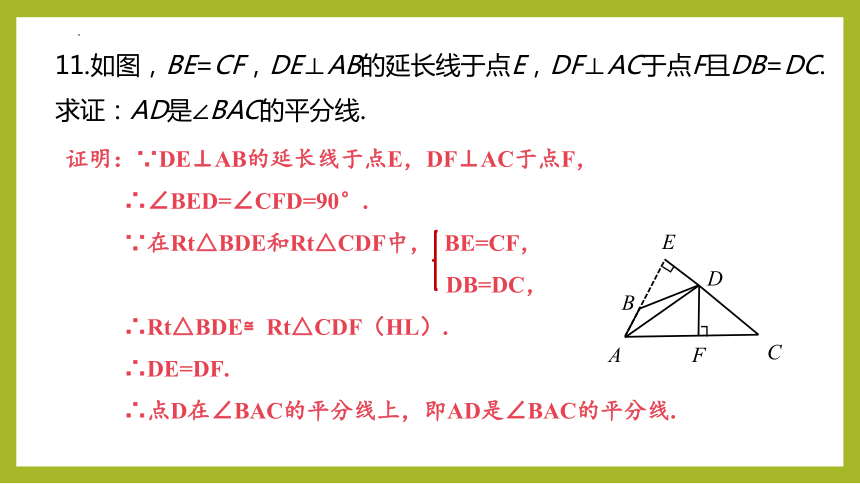
11.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F且DB=DC.求证:AD是∠BAC的平分线.
C
E
A
F
D
B
┐
┐
证明:∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴∠BED=∠CFD=90°.
∵在Rt△BDE和Rt△CDF中, BE=CF,
DB=DC,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF.
∴点D在∠BAC的平分线上,即AD是∠BAC的平分线.
12.如图,在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
E
A
B
C
D
F
┌
┐
证明:∵∠ADC+∠ABC=180°,∠ADC+∠EDC=180°, ∴∠ABC=∠EDC.
∵CE⊥AD,CF⊥AB, ∴∠CED=∠CFB=90°.
∵在△BCF和△DCE中, ∠CFB=∠CED,
∠FBC=∠EDC,
BC=DC,
∴△BCF≌△DCE(AAS).
∴CF=CE,即AC平分∠BAD.
D
13.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE是∠DAB 的平分线.
证明:过点E作EF⊥AD于点F,
∵∠B=∠C=90°, ∴DC⊥EC,EB⊥AB.
∵DE平分∠ADC, ∴EC=EF.
∵E是BC的中点, ∴EC=EB.
又∵EF⊥AD,EB⊥AB,
∴点E在∠BAD的平分线上,即AE是∠DAB的平分线.
A
B
C
E
D
┌
┌
F
14.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:△ABE≌△CBF.
证明:∵∠ABC=90°,∠ABC+∠CBF=180°,
∴∠CBF=90°.
在Rt△ABE和Rt△CBF中,
AE=CF,
AB=CB,
∴Rt△ABE≌Rt△CBF(HL).
考点07 判定直角三角形全等
15.如图,点B,E,F,C在同一条直线上,AE⊥BC,DF⊥BC,AB=DC,BE=CF.试判断AB与CD的位置关系,并证明.
解:AB//CD,理由如下:
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°
∵在Rt△ABE和Rt△DCF中, AB=DC,
BE=CF,
∴ Rt△ABE≌Rt△DCF(HL).
∴∠B=∠C,则AB//CD.
C
A
B
D
E
F
D
16.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,P,Q两点分别在AC上和过点A且垂直AC的射线AM上运动,且PQ=AB.当点P运动到AC上什么位置时,△ABC与△QPA全等?
分析:△ABC和△QPA是直角三角形,题目中已经有一边相等.
①因为AB,PQ分别为Rt△ABC和Rt△QAP的斜边,可以令“BC=AP”,选择“HL”.
②因为AB,PQ分别为Rt△ABC和Rt△QAP的斜边,可以令“AC=AP”,选择“HL”.
D
解:①当点P运动到AP=BC的位置时,
在Rt△APQ和Rt△CBA中,
PQ=BA,
AP=BC,
∴Rt△APQ≌Rt△CBA(HL).
∴AP=BC=5cm.
D
解:②当点P运动到AP=AC的位置时,
Rt△APQ和Rt△CBA中,
PQ=AB,
AP=CA,
∴Rt△APQ≌Rt△CAB(HL).
∴AP=AC=10cm.
综上,当点P运动到使AP=5cm或者10cm位置时,
△APQ和△CAB全等.
17 [2022·浙江湖州中考]如图,在6×6的正方形(正方形ABCD)网格中,每个小正方形的边长为1,每个小正方形的顶点称为格点.M,N分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连接PM,PN,则在所有满足∠MPN=45°的△PMN中,边PM的长的最大值是( C )
A.4
B.6
C.2
D.3
(第4题图)
C
2个定理
考点08 勾股定理
(第4题答图)
解析:如答图,△MNP为等腰直角三角形,∠MPN=45°,此时PM最长.根据勾股定理,得PM=????????+????????=????????=2????????.故选C.
?
(第4题答图)
18.[2021·四川自贡中考]如图,A(8,0),C(-2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( D )
A.(0,5)
B.(5,0)
C.(6,0)
D.(0,6)
(第5题图)
解析:根据已知,得AB=AC=10,OA=8.在Rt△ABO中,∵OB=?????????????????????????=6,∴B(0,6).故选D.
?
D
考点09 勾股定理的逆定理
19.[2022·河北石家庄模拟]如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五块正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按如图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( B )
A.1,4,5
B.2,3,5
C.3,4,5
D.2,2,4
(第6题图)
B
解析:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是????×????????=????????=1;当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是????×????????=????????;当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是????×????????=????????=1.∵????????>????????,∴选取的三块纸片的面积分别是2,3,5.故选B.
?
20.[2022·江苏盐城模拟]如图是正方形网格,则∠BAC+∠CDE=? 45° ?(A,B,C,D,E是网格线的交点).?
(第7题图)
45°
(第7题答图)
解析:设小正方形的边长是1,连接AD,如答图.
∵AD=????????+????????=????????,CD=????????+????????=????????,AC=????????+????????=????????,∴AD=CD,AD2+CD2=AC2,∴∠ADC=90°,∴△ADC是等腰直角三角形,∴∠DAC=∠DCA=45°.∵AB∥DE,∴∠BAC+∠DAC+∠ADC+∠CDE=180°,∴∠BAC+∠CDE=45°.
?
(第7题答图)
2个应用
考点10 勾股定理的应用
21 [2022·浙江金华中考]如图是城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是(3,1),(4,-2),下列各地点,离原点最近的是( A )
A.超市
B.医院
C.体育场
D.学校
(第8题图)
A
解析:如答图,点O到超市的距离为????????+????????=????,点O到学校的距离为????????+????????=????????,点O到体育场的距离为????????+????????=????????,点O到医院的距离为????????+????????=????????.∵????<????????=????????<????????,∴离原点最近的是超市.故选A.
?
(第8题答图)
(第8题答图)
22.数学文化 中国非物质文化 [2022·江苏泰州中考]如图的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为? ???? ?.?
?
(第9题图)
????
?
(第9题答图)
解析:如答图,第一步走到①,第二步走到②.故走两步后的落点与出发点间的最短距离为????????+????????=????.
?
(第9题答图)
考点11 勾股定理的逆定理的应用
23. [2022·广东茂名模拟]如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花.经测量,∠EDC=90°,DC=6 m,CE=10 m,BD=14 m,AB=16 m,AE=2 m.
(1)求DE的长;
解:(1)在Rt△EDC中,
∵∠EDC=90°,DC=6 m,CE=10 m,
∴ED=?????????????????????=8(m).
?
(第10题图)
(2)求四边形ABDE的面积.
解:(2)如答图,连接BE.
在Rt△EBD中,∵BD=14 m,ED=8 m,
∴BE2=BD2+ED2=142+82=260(m2).
∵AB=16 m,AE=2 m,
∴AB2+AE2=162+22=260(m2),∴AB2+AE2=BE2,
∴△ABE是直角三角形,且∠A=90°,
∴S△ABE=????????AB·AE=????????×16×2=16(m2).
又∵S△BDE=????????BD·DE=????????×14×8=56(m2),
∴S四边形ABDE=S△ABE+????△????????????=72(m2).
?
(第10题图)
(第10题答图)
(第10题答图)
2种数学思想的运用
考点12 分类讨论思想的运用
24.[2022·广西百色中考]活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.例如,已知在△ABC中,∠A=30°,AC=3,∠A所对的边为3,满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为( C )
?
A.2
B.2-3
C.2或
D.2或2-3
(第11题图)
C
(第11题答图)
解析:如答图,过点C作CH⊥AB于点H,在AB上取一点D,使CD=CB,则DH=BH.∵∠A=30°,∴CH=????????AC=????????,AH=?????????????????????????=???????? ????.在Rt△CBH中,由勾股定理,得BH=?????????????????????????=?????????????=????????,∴AB=AH+BH=????????????+????????=2????,AD=AH-DH=????????????-????????=????.故选C.
?
(第11题答图)
25. [2022·黑龙江牡丹江模拟]腰长为5,高为4的等腰三角形的底边长是? 6或2????或4???? ?.?
?
解析:①如答图(1),当AB=AC=5,AD=4时,BD=CD=3,∴此时底边长为6;②如答图(2),当AB=AC=5,CD=4时,AD=3,∴BD=2,∴BC=????????+????????=2????,∴此时底边长为2????;③如答图(3),当AB=AC=5,CD=4时,AD=?????????????????????????=3,∴BD=8,∴BC=????????+????????=4????,∴此时底边长为4????.综上可知,腰长为5,高为4的等腰三角形的底边长是6或2????或4????.
?
6或2????
?
或4????
?
(第12题答图)
(第12题答图)
考点13 方程思想的运用
26. 数学文化 中国数学古典 [2021·江苏宿迁中考]《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问:水深、葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面的部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图),问:水深、芦苇长各多少尺?该问题中的水深是? 12 ?尺.?
12
(第13题图)
(第13题答图)
(第13题答图)
解析:依题意画出图形,如答图.设芦苇长AC=AC'=x尺,则水深AB=(x-1)尺.∵C'E=10尺,∴C'B=5尺.在Rt△AC'B中,52+(x-1)2=x2,解得x=13,∴x-1=12.故芦苇长13尺,水深是12尺.
(1)过点A,并且半径为5cm的圆的圆心的轨迹是 .
(2)底边为线段AB的等腰△ABC的顶点C的轨迹是 .
(3)在等腰三角形内部,到两腰距离相等的点的轨迹是 .
(4) 线段AB=10cm,到A和B的距离和等于10cm的点的轨迹是 .
以A点为圆心,5cm的长为半径的圆
线段AB的垂直平分线(AB的中点D除外)
底边上的高(中线)
线段AB
考点14 轨迹
第 19 章 几何证明
单元复习(4个概念2个性质3个判定2个定理2个应用2种思想方法1个轨迹)
学习目标
1.理解命题、逆命题、定理、逆定理等的含义;
2.掌握证明真命题正确性的方法步骤,会举反例说明假命题的错误;掌握证明线段相等 角度相等的基本方法和思路;
3.理解轨迹的定义,掌握三种基本轨迹;
4.能判断直角三角形全等,能应用勾股定理及其逆定理解决实际问题.
?
1.下列语句是命题吗?如果是,请将它们改写成“如果……,那么……”的形式.并指出条件和结论。
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
如果两条直线被第三条直线所截,那么同旁内角互补;
如果等式两边都加同一个数,那么结果仍是等式;
如果两个数互为相反数,那么这两个数相加得0;
如果两个角是同旁内角,那么这两个角互补;
4个概念
考点01 命题
考点02 互逆命题
1 [2022·上海中考]下列说法正确的是( A )
A.命题一定有逆命题
B.所有的定理一定有逆定理
C.真命题的逆命题一定是真命题
D.假命题的逆命题一定是假命题
A
解析:A.命题一定有逆命题,此选项说法正确;B.不是所有的定理一定有逆定理,如“全等三角形的对应角相等”没有逆定理,此选项说法错误;C.真命题的逆命题不一定是真命题,如“对顶角相等”的逆命题是假命题,此选项说法错误;D.假命题的逆命题不一定是假命题,如假命题“对应角相等的三角形全等”,其逆命题是真命题,此选项说法错误.故选A.
2 [2022·江苏无锡中考]请写出命题“如果a>b,那么b-a<0”的逆命题:? 如果b-a<0,那么a>b ?.?
如
果b-a<0,那么a>b
考点03 公理、定理
3. 下列真命题能作为公理的是 ( )
A.对顶角相等
B.三角形的内角和是180°
C.过一点有且只有一条直线与已知直线垂直
D.内错角相等,两直线平行
4.“经过两点有且只有一条直线”是( )
A.公理 B.假命题
C.定义 D.以上都不是
C
A
5.命题“直角三角形的两个锐角互余”是( )
A.角的定义 B.假命题
C.公理 D.定理
分析:可以用逻辑推理的方法判断此命题是正确的
D
定义、命题、公理、定理之间的区别与联系:
(1)联系:这四者都是命题.
(2)区别:定义、公理、定理都是真命题,都可以作为进一步判断其他命题真假的依据,只不过公理是最原始的依据;而命题不一定是真命题,因而不能作为进一步判断其他命题真假的依据.
考点04 互逆定理
6. [2022·江苏无锡宜兴市二模]下列命题的逆命题成立的是? ①④ ?.?
①同旁内角互补,两直线平行
②等边三角形是锐角三角形
③如果两个实数相等,那么它们的平方相等
①④
④全等三角形的三条边对应相等
解析:①“同旁内角互补,两直线平行”的逆命题为“两直线平行,同旁内角互补”,成立;②“等边三角形是锐角三角形”的逆命题为“锐角三角形是等边三角形”,不成立;③“如果两个实数相等,那么它们的平方相等”的逆命题为“平方相等的两个实数相等”,不成立;④“全等三角形的三条边对应相等”的逆命题为“三条边对应相等的三角形全等”,成立.故答案为①④.
7.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
考点05 线段的垂直平分线
2个性质3个判定
证明:过点Q作MN⊥AB,垂足为点C,
故∠QCA=∠QCB=90°.
在Rt△QCA 和Rt△QCB中,
∵QA=QB,QC=QC,
∴Rt△QCA≌Rt△QCB(H.L.).
∴AC=BC.
∴点Q在线段AB的垂直平分线上.
8.已知: 如图,QA=QB.
求证: 点Q在线段AB的垂直平分线上.
你能根据分析中后一种添加辅助线的方法,写出它的证明过程吗?
证明:∵OP为∠AOB的平分线,PC⊥OA,PD⊥OB,
∴PC=PD.
在Rt△OCP和Rt△ODP中,
∵ OP=OP,
PC=PD,
∴Rt△OCP≌ Rt△ODP(HL).
∴ ∠CPO=∠DPO,OC=OD.
9.如图,OP为∠AOB 的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D,则下列结论错误的是( )
A.PC=PD B.∠CPO=∠DOP C.∠CPO=∠DPO D.OC=OD
B
考点06 角平分线
分析:在△ABC中,∠C=90°, ∴DC⊥AC.
又∵DE⊥AB,AD平分∠CAB, ∴DC=DE.
在Rt△ACD和Rt△AED中, AD=AD,
DC=DE,
∴Rt△ACD≌Rt△AED(HL), ∴AC=AE.
∵AC=BC, ∴AE=BC, ∴△DEB的周长为8cm.
10.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,
DE⊥AB,垂足为E,若AB=8cm,则△DEB 的周长为( )
A.10cm B.7cm C.8cm D.不能确定
C
11.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F且DB=DC.求证:AD是∠BAC的平分线.
C
E
A
F
D
B
┐
┐
证明:∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴∠BED=∠CFD=90°.
∵在Rt△BDE和Rt△CDF中, BE=CF,
DB=DC,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF.
∴点D在∠BAC的平分线上,即AD是∠BAC的平分线.
12.如图,在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
E
A
B
C
D
F
┌
┐
证明:∵∠ADC+∠ABC=180°,∠ADC+∠EDC=180°, ∴∠ABC=∠EDC.
∵CE⊥AD,CF⊥AB, ∴∠CED=∠CFB=90°.
∵在△BCF和△DCE中, ∠CFB=∠CED,
∠FBC=∠EDC,
BC=DC,
∴△BCF≌△DCE(AAS).
∴CF=CE,即AC平分∠BAD.
D
13.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE是∠DAB 的平分线.
证明:过点E作EF⊥AD于点F,
∵∠B=∠C=90°, ∴DC⊥EC,EB⊥AB.
∵DE平分∠ADC, ∴EC=EF.
∵E是BC的中点, ∴EC=EB.
又∵EF⊥AD,EB⊥AB,
∴点E在∠BAD的平分线上,即AE是∠DAB的平分线.
A
B
C
E
D
┌
┌
F
14.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:△ABE≌△CBF.
证明:∵∠ABC=90°,∠ABC+∠CBF=180°,
∴∠CBF=90°.
在Rt△ABE和Rt△CBF中,
AE=CF,
AB=CB,
∴Rt△ABE≌Rt△CBF(HL).
考点07 判定直角三角形全等
15.如图,点B,E,F,C在同一条直线上,AE⊥BC,DF⊥BC,AB=DC,BE=CF.试判断AB与CD的位置关系,并证明.
解:AB//CD,理由如下:
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°
∵在Rt△ABE和Rt△DCF中, AB=DC,
BE=CF,
∴ Rt△ABE≌Rt△DCF(HL).
∴∠B=∠C,则AB//CD.
C
A
B
D
E
F
D
16.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,P,Q两点分别在AC上和过点A且垂直AC的射线AM上运动,且PQ=AB.当点P运动到AC上什么位置时,△ABC与△QPA全等?
分析:△ABC和△QPA是直角三角形,题目中已经有一边相等.
①因为AB,PQ分别为Rt△ABC和Rt△QAP的斜边,可以令“BC=AP”,选择“HL”.
②因为AB,PQ分别为Rt△ABC和Rt△QAP的斜边,可以令“AC=AP”,选择“HL”.
D
解:①当点P运动到AP=BC的位置时,
在Rt△APQ和Rt△CBA中,
PQ=BA,
AP=BC,
∴Rt△APQ≌Rt△CBA(HL).
∴AP=BC=5cm.
D
解:②当点P运动到AP=AC的位置时,
Rt△APQ和Rt△CBA中,
PQ=AB,
AP=CA,
∴Rt△APQ≌Rt△CAB(HL).
∴AP=AC=10cm.
综上,当点P运动到使AP=5cm或者10cm位置时,
△APQ和△CAB全等.
17 [2022·浙江湖州中考]如图,在6×6的正方形(正方形ABCD)网格中,每个小正方形的边长为1,每个小正方形的顶点称为格点.M,N分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连接PM,PN,则在所有满足∠MPN=45°的△PMN中,边PM的长的最大值是( C )
A.4
B.6
C.2
D.3
(第4题图)
C
2个定理
考点08 勾股定理
(第4题答图)
解析:如答图,△MNP为等腰直角三角形,∠MPN=45°,此时PM最长.根据勾股定理,得PM=????????+????????=????????=2????????.故选C.
?
(第4题答图)
18.[2021·四川自贡中考]如图,A(8,0),C(-2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( D )
A.(0,5)
B.(5,0)
C.(6,0)
D.(0,6)
(第5题图)
解析:根据已知,得AB=AC=10,OA=8.在Rt△ABO中,∵OB=?????????????????????????=6,∴B(0,6).故选D.
?
D
考点09 勾股定理的逆定理
19.[2022·河北石家庄模拟]如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五块正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按如图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( B )
A.1,4,5
B.2,3,5
C.3,4,5
D.2,2,4
(第6题图)
B
解析:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是????×????????=????????=1;当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是????×????????=????????;当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是????×????????=????????=1.∵????????>????????,∴选取的三块纸片的面积分别是2,3,5.故选B.
?
20.[2022·江苏盐城模拟]如图是正方形网格,则∠BAC+∠CDE=? 45° ?(A,B,C,D,E是网格线的交点).?
(第7题图)
45°
(第7题答图)
解析:设小正方形的边长是1,连接AD,如答图.
∵AD=????????+????????=????????,CD=????????+????????=????????,AC=????????+????????=????????,∴AD=CD,AD2+CD2=AC2,∴∠ADC=90°,∴△ADC是等腰直角三角形,∴∠DAC=∠DCA=45°.∵AB∥DE,∴∠BAC+∠DAC+∠ADC+∠CDE=180°,∴∠BAC+∠CDE=45°.
?
(第7题答图)
2个应用
考点10 勾股定理的应用
21 [2022·浙江金华中考]如图是城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是(3,1),(4,-2),下列各地点,离原点最近的是( A )
A.超市
B.医院
C.体育场
D.学校
(第8题图)
A
解析:如答图,点O到超市的距离为????????+????????=????,点O到学校的距离为????????+????????=????????,点O到体育场的距离为????????+????????=????????,点O到医院的距离为????????+????????=????????.∵????<????????=????????<????????,∴离原点最近的是超市.故选A.
?
(第8题答图)
(第8题答图)
22.数学文化 中国非物质文化 [2022·江苏泰州中考]如图的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为? ???? ?.?
?
(第9题图)
????
?
(第9题答图)
解析:如答图,第一步走到①,第二步走到②.故走两步后的落点与出发点间的最短距离为????????+????????=????.
?
(第9题答图)
考点11 勾股定理的逆定理的应用
23. [2022·广东茂名模拟]如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花.经测量,∠EDC=90°,DC=6 m,CE=10 m,BD=14 m,AB=16 m,AE=2 m.
(1)求DE的长;
解:(1)在Rt△EDC中,
∵∠EDC=90°,DC=6 m,CE=10 m,
∴ED=?????????????????????=8(m).
?
(第10题图)
(2)求四边形ABDE的面积.
解:(2)如答图,连接BE.
在Rt△EBD中,∵BD=14 m,ED=8 m,
∴BE2=BD2+ED2=142+82=260(m2).
∵AB=16 m,AE=2 m,
∴AB2+AE2=162+22=260(m2),∴AB2+AE2=BE2,
∴△ABE是直角三角形,且∠A=90°,
∴S△ABE=????????AB·AE=????????×16×2=16(m2).
又∵S△BDE=????????BD·DE=????????×14×8=56(m2),
∴S四边形ABDE=S△ABE+????△????????????=72(m2).
?
(第10题图)
(第10题答图)
(第10题答图)
2种数学思想的运用
考点12 分类讨论思想的运用
24.[2022·广西百色中考]活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.例如,已知在△ABC中,∠A=30°,AC=3,∠A所对的边为3,满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为( C )
?
A.2
B.2-3
C.2或
D.2或2-3
(第11题图)
C
(第11题答图)
解析:如答图,过点C作CH⊥AB于点H,在AB上取一点D,使CD=CB,则DH=BH.∵∠A=30°,∴CH=????????AC=????????,AH=?????????????????????????=???????? ????.在Rt△CBH中,由勾股定理,得BH=?????????????????????????=?????????????=????????,∴AB=AH+BH=????????????+????????=2????,AD=AH-DH=????????????-????????=????.故选C.
?
(第11题答图)
25. [2022·黑龙江牡丹江模拟]腰长为5,高为4的等腰三角形的底边长是? 6或2????或4???? ?.?
?
解析:①如答图(1),当AB=AC=5,AD=4时,BD=CD=3,∴此时底边长为6;②如答图(2),当AB=AC=5,CD=4时,AD=3,∴BD=2,∴BC=????????+????????=2????,∴此时底边长为2????;③如答图(3),当AB=AC=5,CD=4时,AD=?????????????????????????=3,∴BD=8,∴BC=????????+????????=4????,∴此时底边长为4????.综上可知,腰长为5,高为4的等腰三角形的底边长是6或2????或4????.
?
6或2????
?
或4????
?
(第12题答图)
(第12题答图)
考点13 方程思想的运用
26. 数学文化 中国数学古典 [2021·江苏宿迁中考]《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问:水深、葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面的部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图),问:水深、芦苇长各多少尺?该问题中的水深是? 12 ?尺.?
12
(第13题图)
(第13题答图)
(第13题答图)
解析:依题意画出图形,如答图.设芦苇长AC=AC'=x尺,则水深AB=(x-1)尺.∵C'E=10尺,∴C'B=5尺.在Rt△AC'B中,52+(x-1)2=x2,解得x=13,∴x-1=12.故芦苇长13尺,水深是12尺.
(1)过点A,并且半径为5cm的圆的圆心的轨迹是 .
(2)底边为线段AB的等腰△ABC的顶点C的轨迹是 .
(3)在等腰三角形内部,到两腰距离相等的点的轨迹是 .
(4) 线段AB=10cm,到A和B的距离和等于10cm的点的轨迹是 .
以A点为圆心,5cm的长为半径的圆
线段AB的垂直平分线(AB的中点D除外)
底边上的高(中线)
线段AB
考点14 轨迹
