数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率 课件(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率 课件(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 07:14:31 | ||
图片预览



文档简介
(共16张PPT)
直线的倾斜角与斜率
情景引入
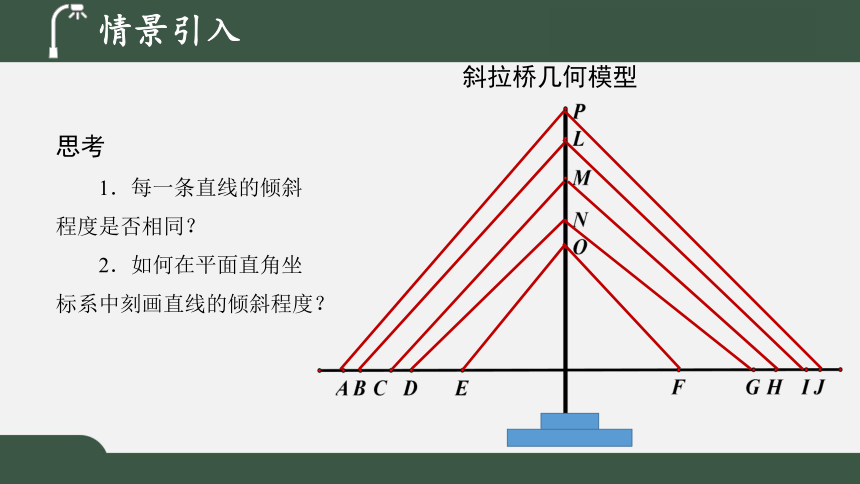
2020年11月12日,中国交建与中国铁建共同拿下拉美地区最长跨海斜拉桥。
情景引入
斜拉桥几何模型
思考
1.每一条直线的倾斜程度是否相同?
2.如何在平面直角坐标系中刻画直线的倾斜程度?
自主学习与小组合作探究
请各位同学带着以下3个问题自学教材,小组合作交流并解决问题,同时注意挖掘重点,然后由小组代表展示.
时间:5分钟
1
2
3
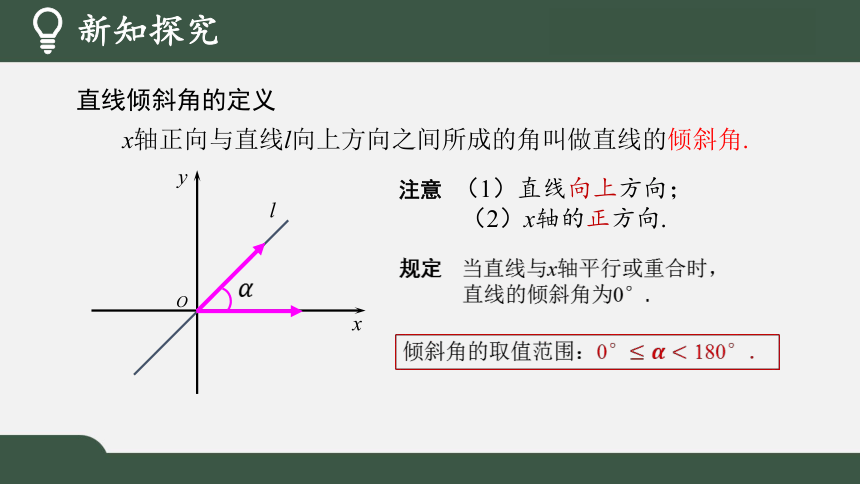
新知探究
x轴正向与直线l向上方向之间所成的角叫做直线的倾斜角.
注意 (1)直线向上方向;
(2)x轴的正方向.
规定 当直线与x轴平行或重合时,
直线的倾斜角为0°
倾斜角的取值范围:0°
O
x
y
l
直线倾斜角的定义
新知探究
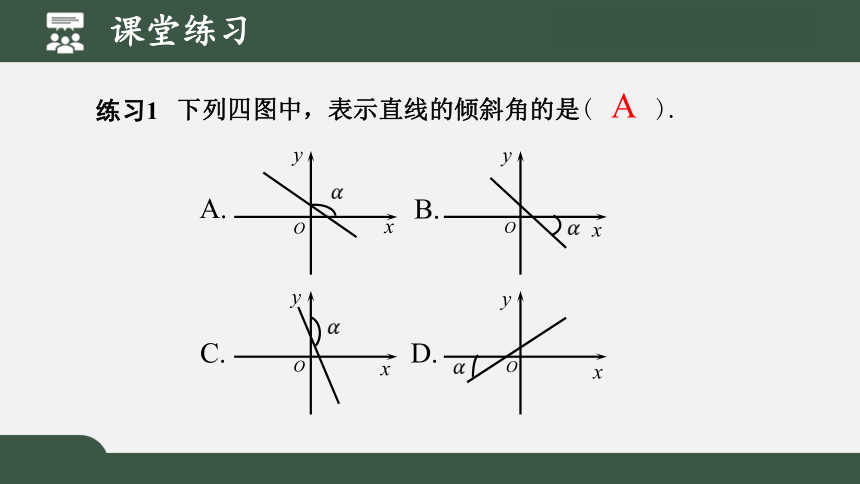
课堂练习
练习1
下列四图中,表示直线的倾斜角的是( ).
A.
B.
C.
D.
A
O
O
O
O
x
x
x
x
y
y
y
y
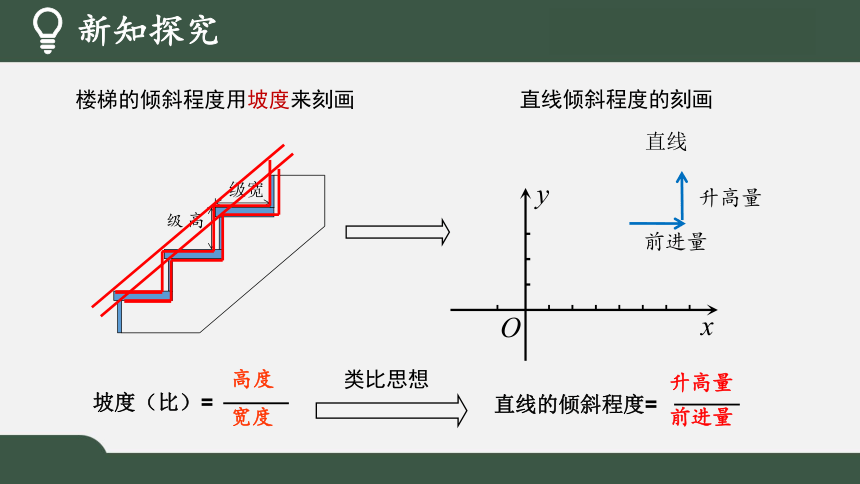
级宽
高级
直线倾斜程度的刻画
升高量
前进量
直线
x
y
O
直线的倾斜程度=
升高量
前进量
坡度(比)=
高度
宽度
楼梯的倾斜程度用坡度来刻画
类比思想
新知探究
x
y
O
A
B
我们把一条直线倾斜角的正切值叫做这条直线的斜率.
直线的斜率
升高量
前进量
新知探究
课堂练习
倾斜角
斜率
练习2 请同学们根据直线斜率的定义,完善以下表格.
0
1
-1
不存在
1. <α<时,斜率k取值范围是__________.
思考
2.<α< 时,斜率k取值范围是__________.
倾斜角为锐角时,斜率随着倾斜角的增大而增大.
倾斜角为钝角时,斜率随着倾斜角的增大而增大.
从“形”研究直线的倾斜角与斜率的关系
新知探究
直线的情况 平行于x轴 由左向右上升 垂直于x轴 由左向右下降
图像
的取值
k的范围
k的单调性
递增
递增
不存在
从“数”研究直线的倾斜角与斜率的关系
新知探究
课堂练习
练习3 图中的直线的斜率分别是
它们斜率的大小关系是什么?
l1
l2
l3
x
y
O
已知两点 P(,), Q(,),如果 ≠
则直线 PQ的斜率为:
x
y
O
过两点的直线的斜率:
纵坐标的差
横坐标的差
y
x
, )
, )
思考
1. 时,直线的位置怎样,k值如何 ?
2.运用上述公式计算直线PQ的斜率时,需要考虑P,Q的顺序和位置吗?
不存在
不需要
新知探究
典例讲解
例题 如图,直线都经过点P(2,3) ,又
分别经过
讨论斜率的是否存在,如存在,求出直线的斜率.
x
y
o
l1
l2
l3
l4
P
Q1
Q2
Q3
Q4
=1
=-1
=0
斜率不存在
解
直线的斜率
=
=
=
直线的斜率不存在.
直线的斜率
直线的斜率
步骤 ①当=,斜率不存在;
② 当≠,直接代入斜率公式.
总结反思
二、方法层面
数学思想 数形结合思想、分类与整合思想、化归与转化思想.
一、知识层面
1.直线倾斜角的定义:
x轴正向与直线l向上方向之间所成的角叫做直线的倾斜角.
2.直线斜率定义及公式:.
3.直线的倾斜角与斜率之间的关系.
课后作业
1.(基础)根据下面各直线满足的条件,分别求出直线的斜率.
(1)倾斜角为;
(2)直线过点A(2,3)与点B(0 , 5).
2.(变式)如果过点P(0,-2)的直线与线段AB相交,已知A(-2,3) ,B(3,2) ,
求直线斜率的取值范围.
3.(拓展)已知直线过点A(8,6),且直线的倾斜角是直线的倾
斜角的一半,求直线的方程.
直线的倾斜角与斜率
情景引入
2020年11月12日,中国交建与中国铁建共同拿下拉美地区最长跨海斜拉桥。
情景引入
斜拉桥几何模型
思考
1.每一条直线的倾斜程度是否相同?
2.如何在平面直角坐标系中刻画直线的倾斜程度?
自主学习与小组合作探究
请各位同学带着以下3个问题自学教材,小组合作交流并解决问题,同时注意挖掘重点,然后由小组代表展示.
时间:5分钟
1
2
3
新知探究
x轴正向与直线l向上方向之间所成的角叫做直线的倾斜角.
注意 (1)直线向上方向;
(2)x轴的正方向.
规定 当直线与x轴平行或重合时,
直线的倾斜角为0°
倾斜角的取值范围:0°
O
x
y
l
直线倾斜角的定义
新知探究
课堂练习
练习1
下列四图中,表示直线的倾斜角的是( ).
A.
B.
C.
D.
A
O
O
O
O
x
x
x
x
y
y
y
y
级宽
高级
直线倾斜程度的刻画
升高量
前进量
直线
x
y
O
直线的倾斜程度=
升高量
前进量
坡度(比)=
高度
宽度
楼梯的倾斜程度用坡度来刻画
类比思想
新知探究
x
y
O
A
B
我们把一条直线倾斜角的正切值叫做这条直线的斜率.
直线的斜率
升高量
前进量
新知探究
课堂练习
倾斜角
斜率
练习2 请同学们根据直线斜率的定义,完善以下表格.
0
1
-1
不存在
1. <α<时,斜率k取值范围是__________.
思考
2.<α< 时,斜率k取值范围是__________.
倾斜角为锐角时,斜率随着倾斜角的增大而增大.
倾斜角为钝角时,斜率随着倾斜角的增大而增大.
从“形”研究直线的倾斜角与斜率的关系
新知探究
直线的情况 平行于x轴 由左向右上升 垂直于x轴 由左向右下降
图像
的取值
k的范围
k的单调性
递增
递增
不存在
从“数”研究直线的倾斜角与斜率的关系
新知探究
课堂练习
练习3 图中的直线的斜率分别是
它们斜率的大小关系是什么?
l1
l2
l3
x
y
O
已知两点 P(,), Q(,),如果 ≠
则直线 PQ的斜率为:
x
y
O
过两点的直线的斜率:
纵坐标的差
横坐标的差
y
x
, )
, )
思考
1. 时,直线的位置怎样,k值如何 ?
2.运用上述公式计算直线PQ的斜率时,需要考虑P,Q的顺序和位置吗?
不存在
不需要
新知探究
典例讲解
例题 如图,直线都经过点P(2,3) ,又
分别经过
讨论斜率的是否存在,如存在,求出直线的斜率.
x
y
o
l1
l2
l3
l4
P
Q1
Q2
Q3
Q4
=1
=-1
=0
斜率不存在
解
直线的斜率
=
=
=
直线的斜率不存在.
直线的斜率
直线的斜率
步骤 ①当=,斜率不存在;
② 当≠,直接代入斜率公式.
总结反思
二、方法层面
数学思想 数形结合思想、分类与整合思想、化归与转化思想.
一、知识层面
1.直线倾斜角的定义:
x轴正向与直线l向上方向之间所成的角叫做直线的倾斜角.
2.直线斜率定义及公式:.
3.直线的倾斜角与斜率之间的关系.
课后作业
1.(基础)根据下面各直线满足的条件,分别求出直线的斜率.
(1)倾斜角为;
(2)直线过点A(2,3)与点B(0 , 5).
2.(变式)如果过点P(0,-2)的直线与线段AB相交,已知A(-2,3) ,B(3,2) ,
求直线斜率的取值范围.
3.(拓展)已知直线过点A(8,6),且直线的倾斜角是直线的倾
斜角的一半,求直线的方程.
