数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和公式(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和公式(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 20.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
等差数列的前n项和
情景引入
我国古代《张邱建算经》中有“分钱问题”改编如下:今有与人钱,初一人与一钱,次一人与二钱,次人与三钱,以次与之,转多一钱,共有百人,问共与几钱?
意思是:今天有人来给钱,第一个人给一钱,第二个人给两钱,第三个人给三钱,以此类推,问:一百人总共需给多少钱?
1+2+3+…+100 =?
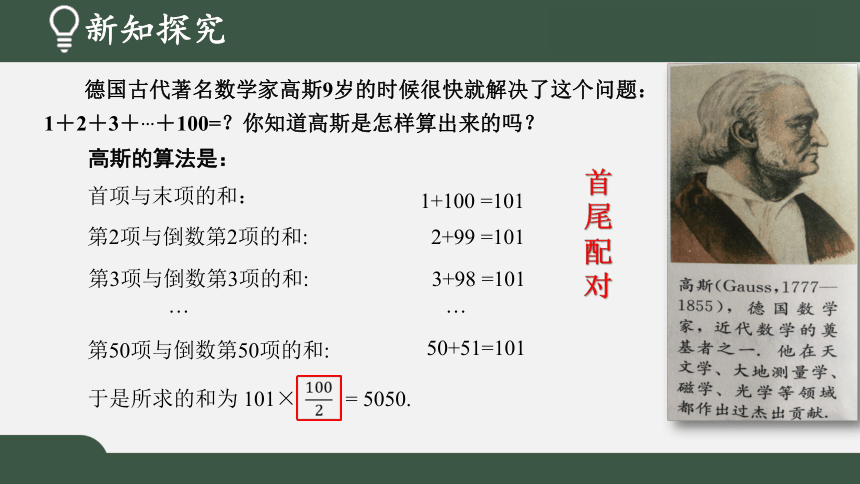
德国古代著名数学家高斯9岁的时候很快就解决了这个问题:1+2+3+…+100=?你知道高斯是怎样算出来的吗?
高斯的算法是:
首项与末项的和:
第2项与倒数第2项的和:
第3项与倒数第3项的和:
第50项与倒数第50项的和:
…
于是所求的和为 101× = 5050.
1+100 =101
2+99 =101
3+98 =101
50+51=101
首
尾
配
对
新知探究
…
【思路一 】
首项与末项的和:
第2项与倒数第2项的和:
第3项与倒数第3项的和:
(1)当n为偶数时,
则可以配凑为,每一对之和为 1+n,
… …
于是所求的和为 (1+n)× =
1+n
2+(n-1) =1+n
3+(n-2) =1+n
新知探究
思考:若不能配凑为整数,怎么处理?
问题1:如何求
(2)当为奇数时,
方法一
.
方法二
.
新知探究
问题1:如何求
故.
先倒序,再相加
新知探究
问题1:如何求
【思路二 】
问题2:已知数列{}是等差数列,如何求
由 ①,
②,
倒序相加法
两式相加,可得,
所以(公式1).
将通项公式代入公式1,
可得(公式2).
由等差数列性质得,= .
新知探究
先自主推导,再小组讨论,讨论结束后请小组代表上台展示,时间为5分钟.
等差数列{}的前n项和公式
概念解读
公式1
公式2
思考 请同学们发挥想象力,思考等差数列的前n项和公式与几何图形之间有和联系?能否帮助我们记忆公式.
等差数列{}的前n项和公式的认识
公式1
公式2
补形成一个平行四边形
分割成一个平行四边形和一个三角形
概念解读
新知探究
结合教材谈一谈你对等差数列两个求和公式的理解?
小组合作探究
等差数列{}的前n项和公式
.
1.公式1反映了等差数列的任意第项与倒数第项的和等于首项与末项之和这个内在联系;公式2反映了等差数列的前项和与它的首项、公差之间的关系其是关于的二次函数,没有常数项.
2. 两个公式在实际应用时的选择.
已知条件 公式选择
,, 公式1
, , 公式2
概念解读
例1 求数列的前项和.
典例讲解
分析 其中等差数列涉及的基本量用表格表示如下:
? ?
解 方法1:
由公式2,可得 .
方法2:
由等差数列通项公式,
由公式1,可得.
变式训练1 等差数列的前多少项和为?
54
解 由公式2,可得 4,
解得 =9.
方法一:
由公式1,可得54解得=22.
方法二:
由等差数列通项公式,可得 4,解得 =22.
典例讲解
变式训练2
已知等差数列的前n项和为求.
2 16
解 由公式1,可得 16,
解得,
因为 ,即,
解得 4.
a1,an,Sn,n,d
知三可求二
典例讲解
等差数列前n项和公式:
总结反思
二、思想方法层面总结:
数学方法 倒序相加法;
数学思想 数形结合,函数与方程思想,化归与转化思想.
一、知识层面总结:
课后作业
1. (基础)已知的前n项和为.
(1)若求;
(2)若,求.
2. (变式)已知是等差数列,前n项和为,且求.
3. (拓展)法国著名数学家棣莫弗一生热爱数学,他梦想在大学当一名教授,但一直未能如愿。他于1754年去世,他的死是一个奇迹,因为在他去世前不久就声称自己每天比前一天多睡15分钟,但他睡满24小时那天,就是他生命的终点,谁料这个预言却成真了。假设他在1754年的10月1日说的这个语言,且当天他的睡眠时间为8小时,请问他去世于哪一天?从开始执行计划之日起直至去世,他一共睡了多少个小时?
等差数列的前n项和
情景引入
我国古代《张邱建算经》中有“分钱问题”改编如下:今有与人钱,初一人与一钱,次一人与二钱,次人与三钱,以次与之,转多一钱,共有百人,问共与几钱?
意思是:今天有人来给钱,第一个人给一钱,第二个人给两钱,第三个人给三钱,以此类推,问:一百人总共需给多少钱?
1+2+3+…+100 =?
德国古代著名数学家高斯9岁的时候很快就解决了这个问题:1+2+3+…+100=?你知道高斯是怎样算出来的吗?
高斯的算法是:
首项与末项的和:
第2项与倒数第2项的和:
第3项与倒数第3项的和:
第50项与倒数第50项的和:
…
于是所求的和为 101× = 5050.
1+100 =101
2+99 =101
3+98 =101
50+51=101
首
尾
配
对
新知探究
…
【思路一 】
首项与末项的和:
第2项与倒数第2项的和:
第3项与倒数第3项的和:
(1)当n为偶数时,
则可以配凑为,每一对之和为 1+n,
… …
于是所求的和为 (1+n)× =
1+n
2+(n-1) =1+n
3+(n-2) =1+n
新知探究
思考:若不能配凑为整数,怎么处理?
问题1:如何求
(2)当为奇数时,
方法一
.
方法二
.
新知探究
问题1:如何求
故.
先倒序,再相加
新知探究
问题1:如何求
【思路二 】
问题2:已知数列{}是等差数列,如何求
由 ①,
②,
倒序相加法
两式相加,可得,
所以(公式1).
将通项公式代入公式1,
可得(公式2).
由等差数列性质得,= .
新知探究
先自主推导,再小组讨论,讨论结束后请小组代表上台展示,时间为5分钟.
等差数列{}的前n项和公式
概念解读
公式1
公式2
思考 请同学们发挥想象力,思考等差数列的前n项和公式与几何图形之间有和联系?能否帮助我们记忆公式.
等差数列{}的前n项和公式的认识
公式1
公式2
补形成一个平行四边形
分割成一个平行四边形和一个三角形
概念解读
新知探究
结合教材谈一谈你对等差数列两个求和公式的理解?
小组合作探究
等差数列{}的前n项和公式
.
1.公式1反映了等差数列的任意第项与倒数第项的和等于首项与末项之和这个内在联系;公式2反映了等差数列的前项和与它的首项、公差之间的关系其是关于的二次函数,没有常数项.
2. 两个公式在实际应用时的选择.
已知条件 公式选择
,, 公式1
, , 公式2
概念解读
例1 求数列的前项和.
典例讲解
分析 其中等差数列涉及的基本量用表格表示如下:
? ?
解 方法1:
由公式2,可得 .
方法2:
由等差数列通项公式,
由公式1,可得.
变式训练1 等差数列的前多少项和为?
54
解 由公式2,可得 4,
解得 =9.
方法一:
由公式1,可得54解得=22.
方法二:
由等差数列通项公式,可得 4,解得 =22.
典例讲解
变式训练2
已知等差数列的前n项和为求.
2 16
解 由公式1,可得 16,
解得,
因为 ,即,
解得 4.
a1,an,Sn,n,d
知三可求二
典例讲解
等差数列前n项和公式:
总结反思
二、思想方法层面总结:
数学方法 倒序相加法;
数学思想 数形结合,函数与方程思想,化归与转化思想.
一、知识层面总结:
课后作业
1. (基础)已知的前n项和为.
(1)若求;
(2)若,求.
2. (变式)已知是等差数列,前n项和为,且求.
3. (拓展)法国著名数学家棣莫弗一生热爱数学,他梦想在大学当一名教授,但一直未能如愿。他于1754年去世,他的死是一个奇迹,因为在他去世前不久就声称自己每天比前一天多睡15分钟,但他睡满24小时那天,就是他生命的终点,谁料这个预言却成真了。假设他在1754年的10月1日说的这个语言,且当天他的睡眠时间为8小时,请问他去世于哪一天?从开始执行计划之日起直至去世,他一共睡了多少个小时?
