数学人教A版(2019)必修第一册5.1.1任意角 课件(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.1任意角 课件(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 56.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 07:15:47 | ||
图片预览




文档简介
(共23张PPT)
人教A(2019)版 必修一 第五章 5.1.1
任 意 角
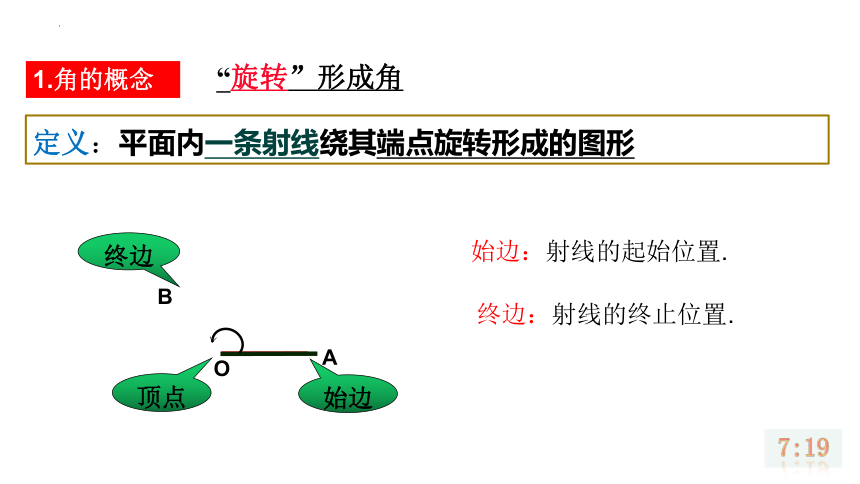
问题1:在现实生活中有没有不在范围内的角?问题2:时钟校准问题(1)假如时钟慢了5分钟,如何校准?请描述校准后分针所转的角度。问题(2)假如时钟快了5分钟,如何校准?请描述校准后分针所转的角度。要准确的刻画“时钟校准”的方法:不仅要考虑旋转的角度,还要考虑旋转方向。刻画角OAB始边终边顶点1.角的概念“旋转”形成角定义:平面内一条射线绕其端点旋转形成的图形终边:射线的终止位置.始边:射线的起始位置.
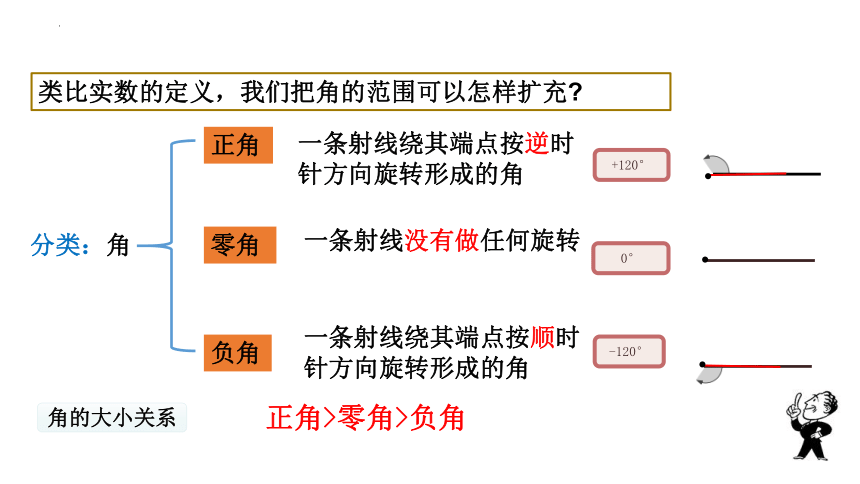
分类:角
正角
一条射线绕其端点按逆时针方向旋转形成的角
一条射线绕其端点按顺时针方向旋转形成的角
零角
一条射线没有做任何旋转
类比实数的定义,我们把角的范围可以怎样扩充
0°
+120°
-120°
负角
正角>零角>负角
角的大小关系
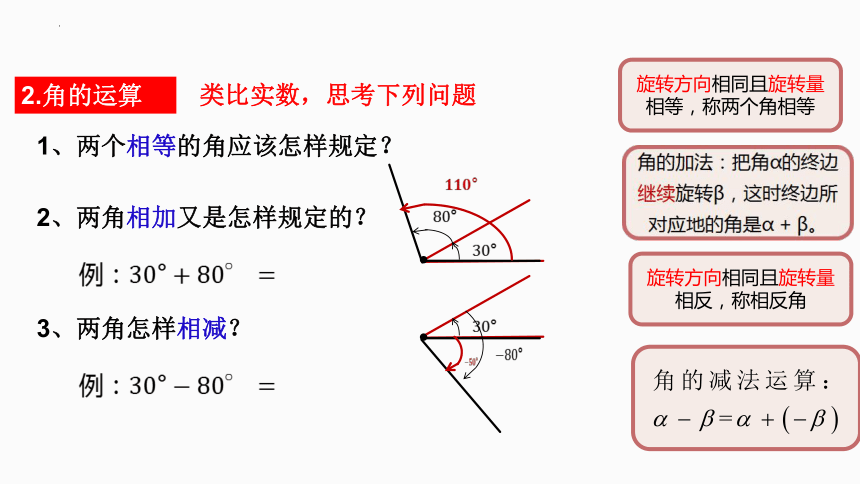
2.角的运算
2、两角相加又是怎样规定的?
类比实数,思考下列问题
例:
3、两角怎样相减?
例:
1、两个相等的角应该怎样规定?
旋转方向相同且旋转量相等,称两个角相等
角的加法:把角的终边继续旋转这时终边所对应地的角是。
旋转方向相同且旋转量相反,称相反角
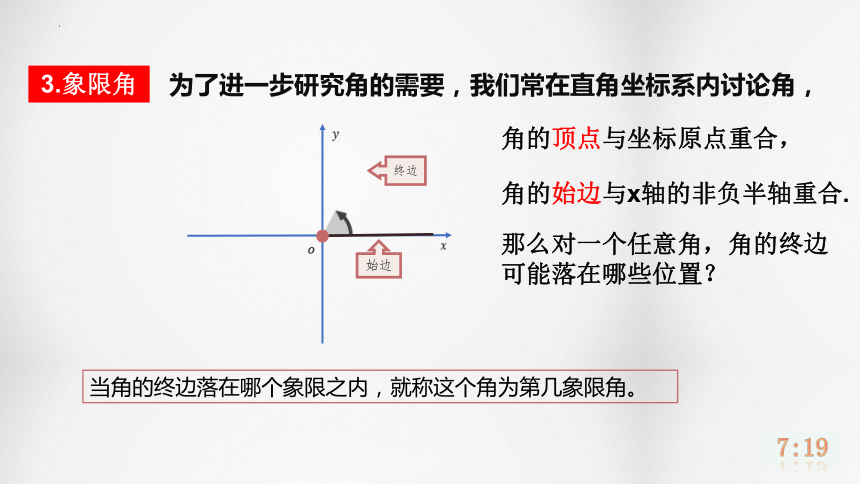
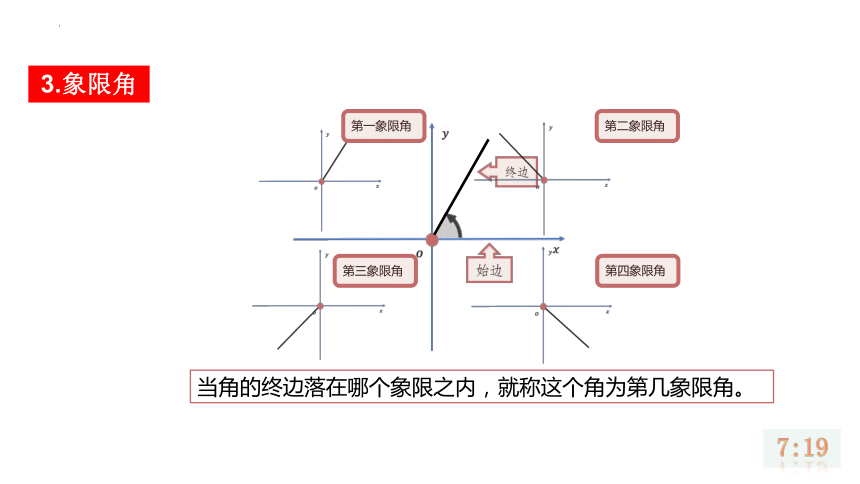
为了进一步研究角的需要,我们常在直角坐标系内讨论角,3.象限角角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合. 始边当角的终边落在哪个象限之内,就称这个角为第几象限角。 终边那么对一个任意角,角的终边可能落在哪些位置?第一象限角第二象限角第三象限角第四象限角当角的终边落在哪个象限之内,就称这个角为第几象限角。3.象限角 始边终边轴线角3.象限角如果角的终边落在坐标轴上,则该角不属于任何一个象限.5958575655545352515049484746454443424140393837363534333231302928272625242322212019181716151413121110090807060504030201000001:开始/重置0059585756555453525150494847464544434241403938373635343332313029282726252423222120191817161514131211100908070605040302010002【练习】在坐标系中画出60°、290°、-200°、-90°,并判断它是第几象限角或轴线角? 第一象限角 第四象限角 第二象限角 轴线角60°290°-200°-90°【练习】在坐标系中画出60°、290°、-200°、-90°,并判断它是第几象限角或轴线角?用图钉联结两根硬纸条,将其中一根固定在OA的位置,将另一根先转动到OB的位置,然后再按照顺时针方向或逆时针方向转动,观察木条重复转到OB的位置时所形成角的特征.合作探究:OAB4.终边相同的角
思考1:观察动画,思考-392°,-32°,328这三个角的终边有何关系?
思考1:思考-392°,-32°,328这三个角的终边有何关系?4.终边相同的角328 =-32 +360 ,-392 =-32+360 .(k=1)(k=-1)(-设射线OB是-32°的终边,则-392°,328°的终边也是OB,这些角与-32°相差360°的整数倍。即这些角可以表示为-32°+k·360°(k∈Z)(1)与-32°角终边重合的角还有哪些?有多少个?4.终边相同的角(2)能不能用集合的形式将它们表达出来?(3)将推广到一般角 ,结论应该是什么? ……-752°688°1048°思考2:一般地,我们有:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角和.4.终边相同的角注意:(1)k∈Z;(2)α是任意角;(3)终边相等的角有无限多个,它们相差360的整数倍.例1:在0°~360°范围内,找出与-950°角终边相同 的角,并判定它是第几象限角.解:-950°=130°-3×360°,所以在0°~360°范围 内,与-950°角终边相同的角是130,它是第二象限角.5958575655545352515049484746454443424140393837363534333231302928272625242322212019181716151413121110090807060504030201000001:开始/重置0059585756555453525150494847464544434241403938373635343332313029282726252423222120191817161514131211100908070605040302010002小组活动:探究:终边在坐标轴上的角的集合该如何表示?探究:终边在坐标轴上的角的集合该如何表示?
小组活动:
组别 角的终边位置 角的集合表示
第一组 在x轴的非负半轴上
第二组 在x轴的非正半轴上
第三组 在y轴的非负半轴上
第四组 在y轴的非正半轴上
第五组 在x轴上
第六组 在y轴上
例2:写出终边在直线y=x上的角的集合S,S中满足不等 式-360°≤β<720°的角β有哪些?解:终边在直线y=x上的角的集合SS={β|β=45°+k·180°,k∈Z};由因k∈Z,故k可能取值为-2,-1,0,1,2,3所以满足条件的角β有-315°、-135°、45°、225°、405°、585°.又因为-360°≤β<720°,所以-360°≤45°+k·180°<720,故-2.25≤k<3.75,1.任意角的概念正角:射线按逆时针方向旋转形成的角负角:射线按顺时针方向旋转形成的角零角:射线不作旋转形成的角置角的顶点于原点始边重合于X轴的非负半轴2.象限角终边落在第几象限就是第几象限角3 .终边与角α相同的角α+k·360°,k∈Z小结反思本次课学习哪些内容?你会解决哪些新问题?1.完成课本171页课后练习题:2.预习教材5.1节“任意角和弧度制”;课后作业
人教A(2019)版 必修一 第五章 5.1.1
任 意 角
问题1:在现实生活中有没有不在范围内的角?问题2:时钟校准问题(1)假如时钟慢了5分钟,如何校准?请描述校准后分针所转的角度。问题(2)假如时钟快了5分钟,如何校准?请描述校准后分针所转的角度。要准确的刻画“时钟校准”的方法:不仅要考虑旋转的角度,还要考虑旋转方向。刻画角OAB始边终边顶点1.角的概念“旋转”形成角定义:平面内一条射线绕其端点旋转形成的图形终边:射线的终止位置.始边:射线的起始位置.
分类:角
正角
一条射线绕其端点按逆时针方向旋转形成的角
一条射线绕其端点按顺时针方向旋转形成的角
零角
一条射线没有做任何旋转
类比实数的定义,我们把角的范围可以怎样扩充
0°
+120°
-120°
负角
正角>零角>负角
角的大小关系
2.角的运算
2、两角相加又是怎样规定的?
类比实数,思考下列问题
例:
3、两角怎样相减?
例:
1、两个相等的角应该怎样规定?
旋转方向相同且旋转量相等,称两个角相等
角的加法:把角的终边继续旋转这时终边所对应地的角是。
旋转方向相同且旋转量相反,称相反角
为了进一步研究角的需要,我们常在直角坐标系内讨论角,3.象限角角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合. 始边当角的终边落在哪个象限之内,就称这个角为第几象限角。 终边那么对一个任意角,角的终边可能落在哪些位置?第一象限角第二象限角第三象限角第四象限角当角的终边落在哪个象限之内,就称这个角为第几象限角。3.象限角 始边终边轴线角3.象限角如果角的终边落在坐标轴上,则该角不属于任何一个象限.5958575655545352515049484746454443424140393837363534333231302928272625242322212019181716151413121110090807060504030201000001:开始/重置0059585756555453525150494847464544434241403938373635343332313029282726252423222120191817161514131211100908070605040302010002【练习】在坐标系中画出60°、290°、-200°、-90°,并判断它是第几象限角或轴线角? 第一象限角 第四象限角 第二象限角 轴线角60°290°-200°-90°【练习】在坐标系中画出60°、290°、-200°、-90°,并判断它是第几象限角或轴线角?用图钉联结两根硬纸条,将其中一根固定在OA的位置,将另一根先转动到OB的位置,然后再按照顺时针方向或逆时针方向转动,观察木条重复转到OB的位置时所形成角的特征.合作探究:OAB4.终边相同的角
思考1:观察动画,思考-392°,-32°,328这三个角的终边有何关系?
思考1:思考-392°,-32°,328这三个角的终边有何关系?4.终边相同的角328 =-32 +360 ,-392 =-32+360 .(k=1)(k=-1)(-设射线OB是-32°的终边,则-392°,328°的终边也是OB,这些角与-32°相差360°的整数倍。即这些角可以表示为-32°+k·360°(k∈Z)(1)与-32°角终边重合的角还有哪些?有多少个?4.终边相同的角(2)能不能用集合的形式将它们表达出来?(3)将推广到一般角 ,结论应该是什么? ……-752°688°1048°思考2:一般地,我们有:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角和.4.终边相同的角注意:(1)k∈Z;(2)α是任意角;(3)终边相等的角有无限多个,它们相差360的整数倍.例1:在0°~360°范围内,找出与-950°角终边相同 的角,并判定它是第几象限角.解:-950°=130°-3×360°,所以在0°~360°范围 内,与-950°角终边相同的角是130,它是第二象限角.5958575655545352515049484746454443424140393837363534333231302928272625242322212019181716151413121110090807060504030201000001:开始/重置0059585756555453525150494847464544434241403938373635343332313029282726252423222120191817161514131211100908070605040302010002小组活动:探究:终边在坐标轴上的角的集合该如何表示?探究:终边在坐标轴上的角的集合该如何表示?
小组活动:
组别 角的终边位置 角的集合表示
第一组 在x轴的非负半轴上
第二组 在x轴的非正半轴上
第三组 在y轴的非负半轴上
第四组 在y轴的非正半轴上
第五组 在x轴上
第六组 在y轴上
例2:写出终边在直线y=x上的角的集合S,S中满足不等 式-360°≤β<720°的角β有哪些?解:终边在直线y=x上的角的集合SS={β|β=45°+k·180°,k∈Z};由因k∈Z,故k可能取值为-2,-1,0,1,2,3所以满足条件的角β有-315°、-135°、45°、225°、405°、585°.又因为-360°≤β<720°,所以-360°≤45°+k·180°<720,故-2.25≤k<3.75,1.任意角的概念正角:射线按逆时针方向旋转形成的角负角:射线按顺时针方向旋转形成的角零角:射线不作旋转形成的角置角的顶点于原点始边重合于X轴的非负半轴2.象限角终边落在第几象限就是第几象限角3 .终边与角α相同的角α+k·360°,k∈Z小结反思本次课学习哪些内容?你会解决哪些新问题?1.完成课本171页课后练习题:2.预习教材5.1节“任意角和弧度制”;课后作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
