北京市重点中学2022-2023学年高一上学期12月阶段练习数学试题(无答案)
文档属性
| 名称 | 北京市重点中学2022-2023学年高一上学期12月阶段练习数学试题(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 338.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 00:00:00 | ||
图片预览

文档简介
北京重点中学2022—2023学年度第一学期高一阶段练习
高一数学试题
考生须知:
1.本试卷共4页,满分100分,考试时间90分钟.
2.试题答案一律填写在答题纸上,在试卷上作答无效.
3.答题纸上用默色字迹钢笔或签字笔作答.
4.考试结束后,请按要求及时将答题纸拍照上传.
一、选择题:本大题共10道小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项符合题目的要求.把正确答案涂写在答题卡上相应的位置.
1.已知集合,,则( )
A. B. C. D.
2.下列函数中,既是偶函数又在上单调递增的函数( )
A. B. C. D.
3.函数的零点所在的一个区间是( )
A. B. C. D.
4.,,三个数的大小关系为( )
A. B.
C. D.
5.某地组织一次中学生若干学科考试,若考试成绩按等级性排列,位次由高到低分为、、、、,各等级人数所占比例依次为:等级15%,等级40%,等级30%,等级14%,等级1%.现采用分层抽样的方法,从参加其中一个学科等级性考试的学生中抽取200人作为样本,则该样本中获得或等级的学生人数为( )
A.110 B.55 C.80 D.90
6.设为常数,函数,若为偶函数,则等于( )
A. B. C.1 D.2
7.若,且,则在下列四个选项中,最大的是( )
A. B. C. D.
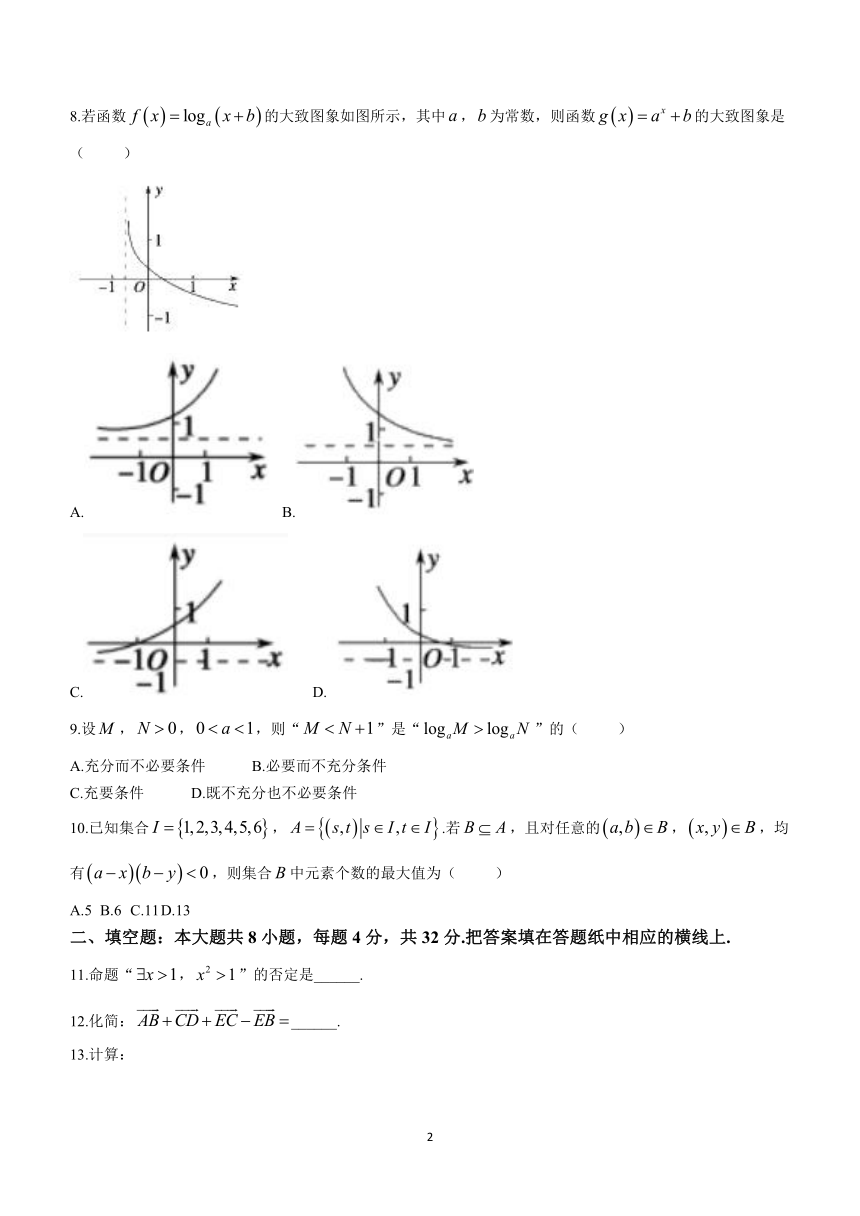
8.若函数的大致图象如图所示,其中,为常数,则函数的大致图象是( )
A. B.
C. D.
9.设,,,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
10.已知集合,.若,且对任意的,,均有,则集合中元素个数的最大值为( )
A.5 B.6 C.11 D.13
二、填空题:本大题共8小题,每题4分,共32分.把答案填在答题纸中相应的横线上.
11.命题“,”的否定是______.
12.化简:______.
13.计算:
(1)______;(2)______.
14.已知的定义域为,则的定义域为______.
15.为保障食品安全,某地食品药监管部门对辖区食品企业进行检查,从甲企业生产的某种同类产品中随机抽取了100件作为样本,并以样本的一项关键质量指标值为检测依据.已知该质量指标值对应的产品等级如下:
质量指标值
等级 次品 二等品 一等品 二等品 三等品 次品
根据质量指标值的分组,统计得到了甲企业的样本频率分布直方图(其中).现从甲企业生产的产品中任取一件,估计该件产品为次品的概率为______.
16.设函数则使得成立的的取值范围是______.
17.在某次国际交流活动中,组织者在某天上午安排了六场专家报告(时间如下,转场时间忽略不计),并要求听报告者不能迟到和早退.
报告名称 A B C D E F
开始时间 8:00 8:10 8:40 8:45 9:15 9:25
结束时间 8:30 9:05 9:30 9:20 10:10 10:10
某单位派甲、乙两人参会,为了获得更多的信息,单位要求甲、乙两人所听报告不相同,且所听报告的总时间尽可能长,那么甲、乙两人应该舍去的报告名称为______.
18.已知函数,,,其中表示,中最大的数.(无理数)
(Ⅰ)若,则______.
(Ⅱ)若对恒成立,则的取值范围是______.
三、解答题:本大题共两题,共28分.
19.(本题14分)某市在寒假中组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记表示学生的考核成绩,并规定为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图:
(Ⅰ)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核成绩为优秀的概率;
(Ⅱ)从图中考核成绩满足的学生中任取2人,求至少有一人考核优秀的概率;
(Ⅲ)记表示学生的考核成绩在区间内的概率,根据以往培训数据,规定当时培训有效.请你根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
20.(本题14分)在直角坐标系中,记函数的图象为曲线,函数的图象为曲线.
(Ⅰ)若,求的值;
(Ⅱ)当曲线在直线的下方时,求的取值范围;
(Ⅲ)证明:曲线和没有交点.
高一数学试题
考生须知:
1.本试卷共4页,满分100分,考试时间90分钟.
2.试题答案一律填写在答题纸上,在试卷上作答无效.
3.答题纸上用默色字迹钢笔或签字笔作答.
4.考试结束后,请按要求及时将答题纸拍照上传.
一、选择题:本大题共10道小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项符合题目的要求.把正确答案涂写在答题卡上相应的位置.
1.已知集合,,则( )
A. B. C. D.
2.下列函数中,既是偶函数又在上单调递增的函数( )
A. B. C. D.
3.函数的零点所在的一个区间是( )
A. B. C. D.
4.,,三个数的大小关系为( )
A. B.
C. D.
5.某地组织一次中学生若干学科考试,若考试成绩按等级性排列,位次由高到低分为、、、、,各等级人数所占比例依次为:等级15%,等级40%,等级30%,等级14%,等级1%.现采用分层抽样的方法,从参加其中一个学科等级性考试的学生中抽取200人作为样本,则该样本中获得或等级的学生人数为( )
A.110 B.55 C.80 D.90
6.设为常数,函数,若为偶函数,则等于( )
A. B. C.1 D.2
7.若,且,则在下列四个选项中,最大的是( )
A. B. C. D.
8.若函数的大致图象如图所示,其中,为常数,则函数的大致图象是( )
A. B.
C. D.
9.设,,,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
10.已知集合,.若,且对任意的,,均有,则集合中元素个数的最大值为( )
A.5 B.6 C.11 D.13
二、填空题:本大题共8小题,每题4分,共32分.把答案填在答题纸中相应的横线上.
11.命题“,”的否定是______.
12.化简:______.
13.计算:
(1)______;(2)______.
14.已知的定义域为,则的定义域为______.
15.为保障食品安全,某地食品药监管部门对辖区食品企业进行检查,从甲企业生产的某种同类产品中随机抽取了100件作为样本,并以样本的一项关键质量指标值为检测依据.已知该质量指标值对应的产品等级如下:
质量指标值
等级 次品 二等品 一等品 二等品 三等品 次品
根据质量指标值的分组,统计得到了甲企业的样本频率分布直方图(其中).现从甲企业生产的产品中任取一件,估计该件产品为次品的概率为______.
16.设函数则使得成立的的取值范围是______.
17.在某次国际交流活动中,组织者在某天上午安排了六场专家报告(时间如下,转场时间忽略不计),并要求听报告者不能迟到和早退.
报告名称 A B C D E F
开始时间 8:00 8:10 8:40 8:45 9:15 9:25
结束时间 8:30 9:05 9:30 9:20 10:10 10:10
某单位派甲、乙两人参会,为了获得更多的信息,单位要求甲、乙两人所听报告不相同,且所听报告的总时间尽可能长,那么甲、乙两人应该舍去的报告名称为______.
18.已知函数,,,其中表示,中最大的数.(无理数)
(Ⅰ)若,则______.
(Ⅱ)若对恒成立,则的取值范围是______.
三、解答题:本大题共两题,共28分.
19.(本题14分)某市在寒假中组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记表示学生的考核成绩,并规定为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图:
(Ⅰ)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核成绩为优秀的概率;
(Ⅱ)从图中考核成绩满足的学生中任取2人,求至少有一人考核优秀的概率;
(Ⅲ)记表示学生的考核成绩在区间内的概率,根据以往培训数据,规定当时培训有效.请你根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
20.(本题14分)在直角坐标系中,记函数的图象为曲线,函数的图象为曲线.
(Ⅰ)若,求的值;
(Ⅱ)当曲线在直线的下方时,求的取值范围;
(Ⅲ)证明:曲线和没有交点.
同课章节目录
