24.6 正多边形与圆同步练习(含解析)
文档属性
| 名称 | 24.6 正多边形与圆同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 981.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.6正多边形与圆沪科版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1.周长相等的正方形与正六边形的面积分别为,,则和的关系为( )
A. B.
C. D.
2.个大小相同的正六边形按如图所示方式紧密排列在同一平面内,、、、、、均是正六边形的顶点,则点是下列哪个三角形的外心.( )
A. B. C. D.
3.如图,设边长为的等边三角形的高、内切圆的半径、外接圆的半径分别为、、,则下列结论不正确的是( )
A. B. C. D.
4.如图,在平面直角坐标系中,边长为的正六边形的中心与原点重台,轴,交轴于点将绕点逆时针旋转,每次旋转,则第次旋转结束时,点的坐标为( )
A.
B.
C.
D.
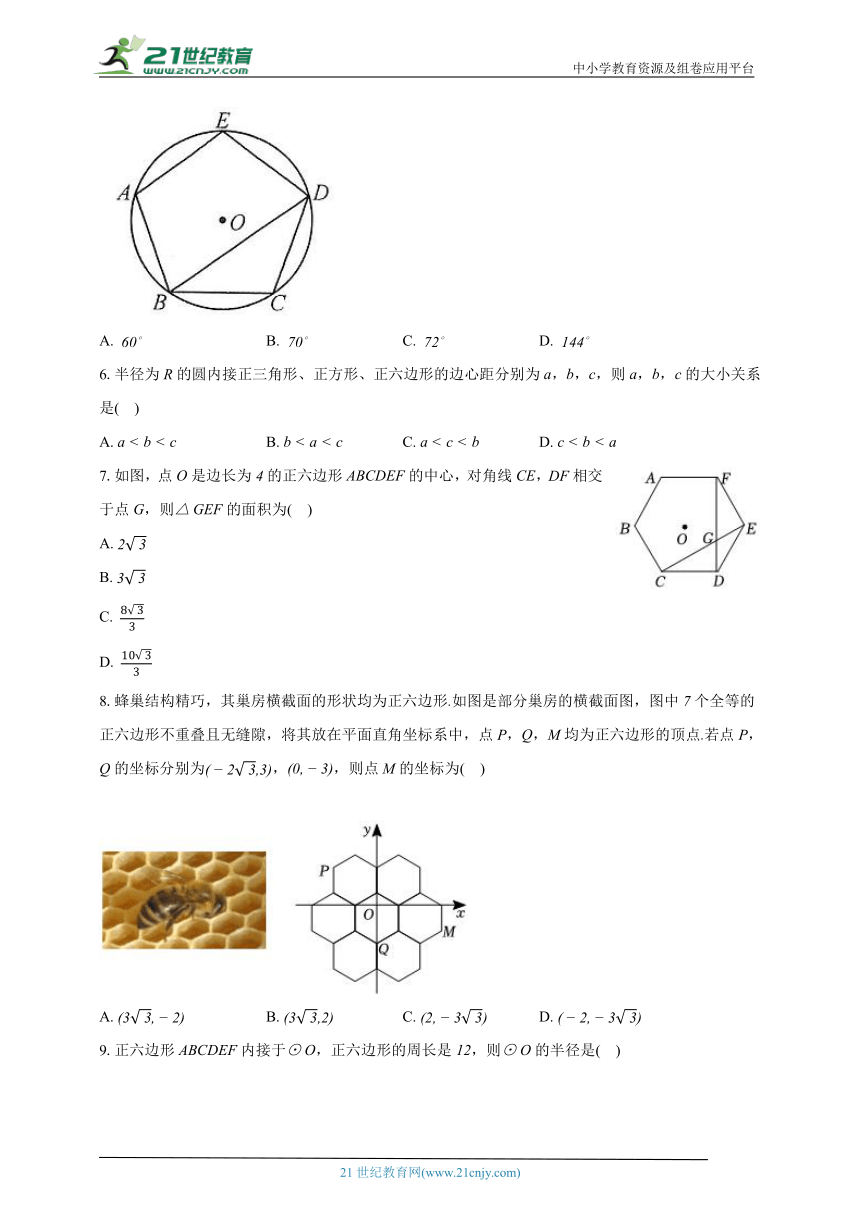
5.如图,已知正五边形内接于,连结,则的度数为( )
A. B. C. D.
6.半径为的圆内接正三角形、正方形、正六边形的边心距分别为,,,则,,的大小关系是( )
A. B. C. D.
7.如图,点是边长为的正六边形的中心,对角线,相交于点,则的面积为( )
A.
B.
C.
D.
8.蜂巢结构精巧,其巢房横截面的形状均为正六边形如图是部分巢房的横截面图,图中个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点,,均为正六边形的顶点若点,的坐标分别为,,则点的坐标为( )
A. B. C. D.
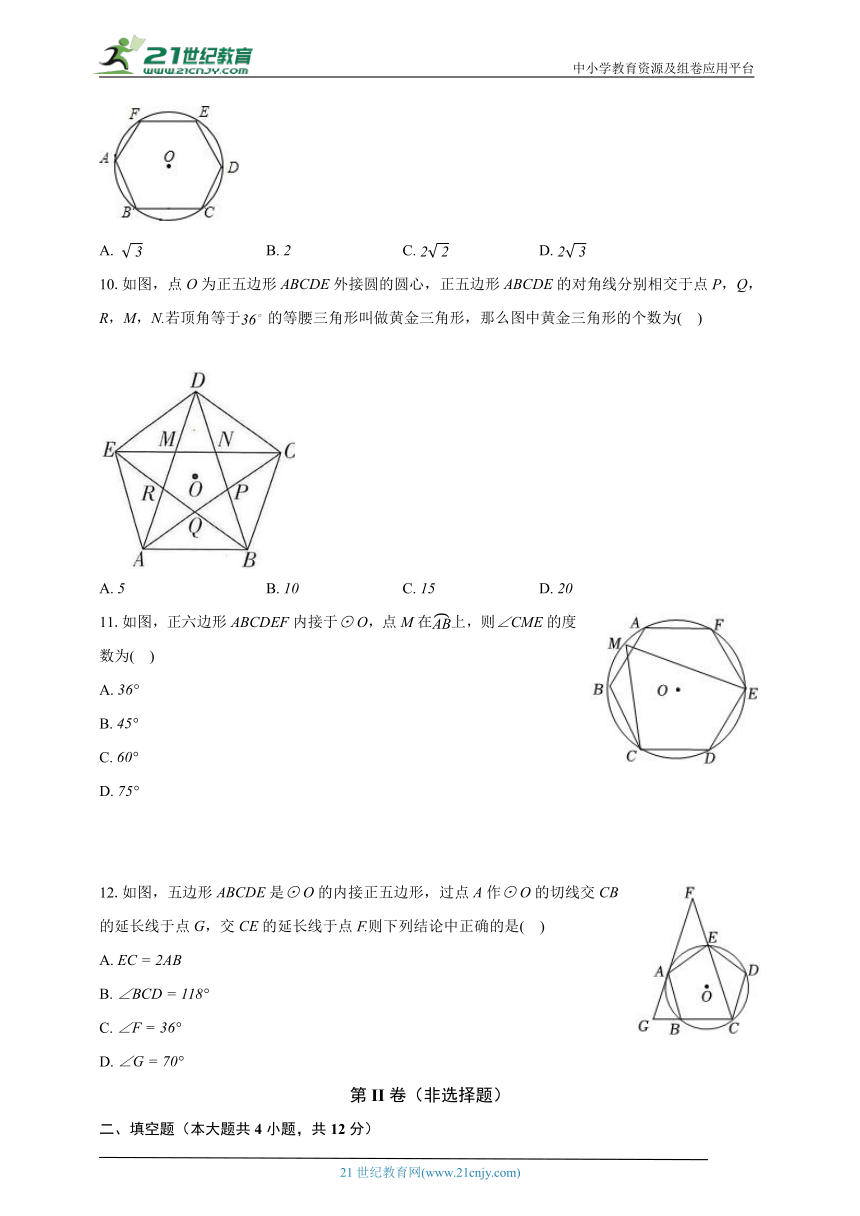
9.正六边形内接于,正六边形的周长是,则的半径是( )
A. B. C. D.
10.如图,点为正五边形外接圆的圆心,正五边形的对角线分别相交于点,,,,若顶角等于的等腰三角形叫做黄金三角形,那么图中黄金三角形的个数为( )
A. B. C. D.
11.如图,正六边形内接于,点在上,则的度数为( )
A.
B.
C.
D.
12.如图,五边形是的内接正五边形,过点作的切线交的延长线于点,交的延长线于点则下列结论中正确的是( )
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
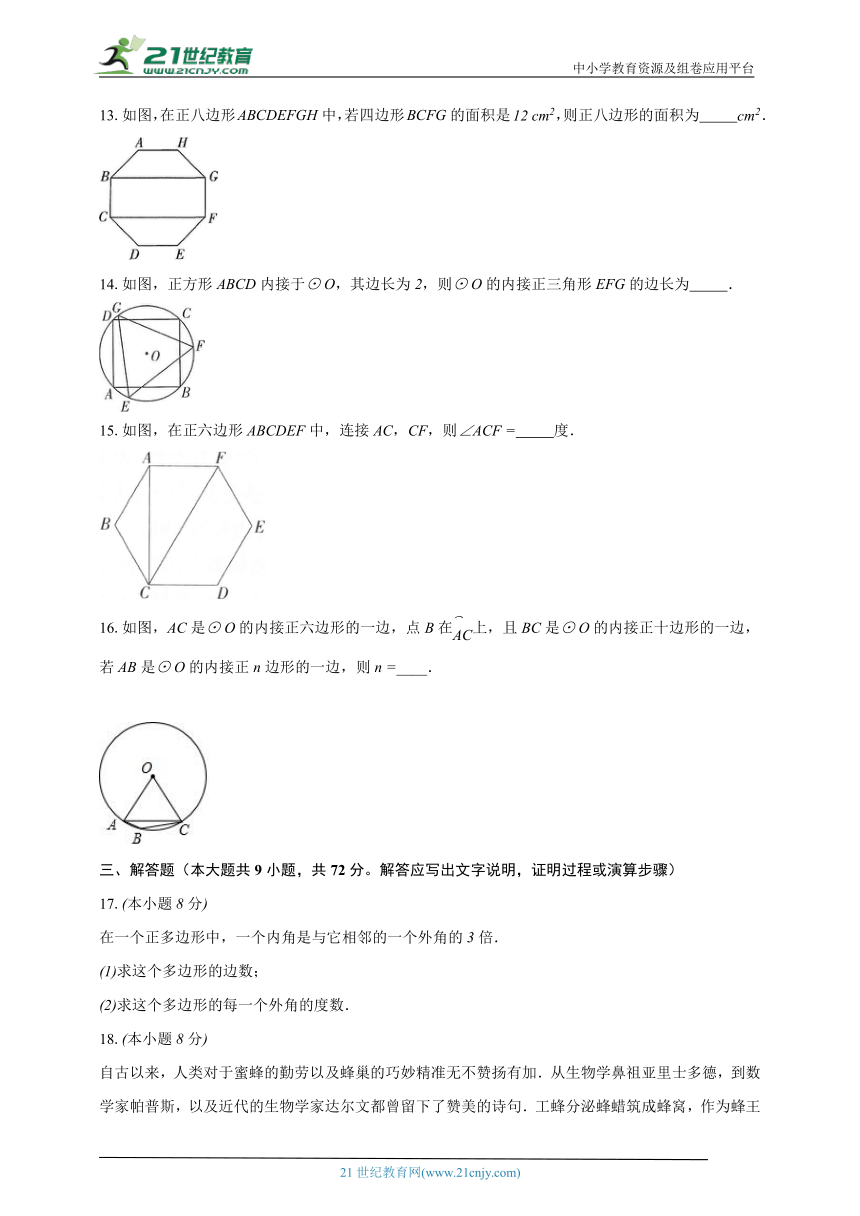
13.如图,在正八边形中,若四边形的面积是,则正八边形的面积为 .
14.如图,正方形内接于,其边长为,则的内接正三角形的边长为 .
15.如图,在正六边形中,连接,,则 度.
16.如图,是的内接正六边形的一边,点在上,且是的内接正十边形的一边,若是的内接正边形的一边,则____.
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
在一个正多边形中,一个内角是与它相邻的一个外角的倍.
求这个多边形的边数;
求这个多边形的每一个外角的度数.
18.本小题分
自古以来,人类对于蜜蜂的勤劳以及蜂巢的巧妙精准无不赞扬有加.从生物学鼻祖亚里士多德,到数学家帕普斯,以及近代的生物学家达尔文都曾留下了赞美的诗句.工蜂分泌蜂蜡筑成蜂窝,作为蜂王产卵、工蜂育幼以及存放蜂蜜、花粉的贮藏室.从正面来看,蜂巢是由许多正六边形连结而成,正六边形是能够不重叠地铺满一个平面的三种正多边形之一,另外两种分别是正方形和正三角形.
一根长的铁丝分别围成正三角形,正方形,正六边形,请同学们直接写出围成图形的面积:______,______,______;
在的条件下,比较围成图形面积的大小;
通过以上计算,当面积一定时,耗材最少的图形是______填:正三角形、正方形、正六边形.
19.本小题分
如图,在网格纸中,、都是格点,以为圆心,为半径作圆.用无刻度的直尺完成以下画图:不写画法
在图中画的一个内接正六边形;
在图中画的一个内接正八边形.
20.本小题分
浦江桃形李是地方名果,是浦江县的特产之一请你运用数学知识,根据素材,帮果农解决问题.
信息及素材
素材一 在专业种植技术人员的正确指导下,果农对桃形李的种植技术进行了研究与改进,使产量得到了增长,根据果农们的记录,年桃形李平均每株产量是千克,年达到了千克,每年的增长率是相同的.
素材二 一般采用的是长方体包装盒.
素材三 果农们通过问卷调查发现,顾客也很愿意购买美观漂亮的其它设计的包装纸盒.
任务:求桃形李产量的年平均增长率;
任务:现有长,宽的长方形纸板,将四角各裁掉一个正方形如图,折成无盖长方体纸盒如图为了放下适当数量的桃形李,需要设计底面积为的纸盒,计算此时纸盒的高;
任务:为了增加包装盒的种类,打算将任务中的纸板通过图的方式裁剪,得到底面为正六边形的无盖纸盒如图,求出此时纸盒的高图中实线表示剪切线,虚线表示折痕纸板厚度及剪切接缝处损耗忽略不计
21.本小题分
门环,在中国绵延了数千多年的,集实用、装饰和门第等级为一体的一种古建筑构件,也成为中国古建“门文化”中的一部分,现有一个门环的示意图如图所示,点为正六边形的中心;
请用无刻度直尺与圆规,过点作一个,使与直线和直线同时相切;请保留作图痕迹
若正六边形的边长为,试求中的半径。结果保留根号
22.本小题分
已知:如图,是的内接等腰三角形,顶角,弦、分别平分、.
求证:五边形是正五边形.
23.本小题分
如图,,,,是上的四个点,.
求证:是等边三角形.
若的半径为,求等边的边心距.
24.本小题分
如图,在正五边形中,为垂足.求证:.
25.本小题分
如图,已知等边,请用直尺不带刻度和圆规按下列要求作图不要求写作法,但要保留作图痕迹
作的外心
设是边上一点,在图中作出一个正六边形,使点、点分别在边和上.
答案和解析
1.【答案】
【解析】设正方形的边长为,则正六边形的边长为,.正六边形的边长为,把正六边形分成六个全等的小正三角形,其高为,,,故选D.
2.【答案】
【解析】本题考查了三角形外心的性质,即到三角形三个顶点的距离相等,依次判断即可.
因为三角形的外心到三角形的三个顶点的距离相等,由正六边形性质可知,点到、、、、的距离中,只有,
所以点是的外心.故选D.
3.【答案】
【解析】如图,是等边三角形,
的内切圆和外接圆是同心圆,圆心为.
设,为切点,连接,,,易得点,,共线,则,,,
,故A正确.
,
.
在中,,即,故B正确.
,,
,
,,故C错误,D正确.
故选C.
4.【答案】
【解析】解:正六边形边长为,中心与原点重合,轴,
,,
:.
第次旋转结束时,点的坐标为;
第次旋转结束时,点的坐标为;
第次旋转结束时,点的坐标为;
第次旋转结束时,点的坐标为.,
次一个循环,
.
第次旋转结束时,点的坐标为.
故选:.
首先确定点的坐标,再根据次一个循环,推出经过第次旋转后,点的坐标即可.
本题考查正多边形的性质,规律型问题,坐标与图形变化旋转等知识,解题的关键是学会探究规律的方法,属于中考常考题型.
5.【答案】
【解析】略
6.【答案】
【解析】【分析】
此题主要考查了正多边形和圆的性质,解决本题的关键是构造直角三角形,得到用半径表示的边心距;注意:正多边形的计算一般要转化为解直角三角形的问题来解决.
根据三角函数即可求解.
【解答】
解:设圆的半径为,
则正三角形的边心距为
正方形的边心距为,
正六边形的边心距为
,
,
故选:.
7.【答案】
【解析】解:六边形是边长为的正六边形,
,,
,
,
,
,
的面积.
故选:.
根据六边形是边长为的正六边形,可得,,根据三角形内角和定理可得,所以,然后利用含度角的直角三角形可得的长,进而可以解决问题.
本题考查了正多边形和三角形的面积,解决本题的关键是掌握正六边形的性质.
8.【答案】
【解析】解:设中间正六边形的中心为,连接.
点,的坐标分别为,,图中是个全等的正六边形,
,,
,
,
,
,,
,
故选:.
设中间正六边形的中心为,连接判断出,的长,可得结论.
本题考查正多边形与圆,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
9.【答案】
【解析】解:连接,,
多边形是正六边形,
,
,
是等边三角形,
,
正六边形的周长是,
,
的半径是,
故选B.
连接,,根据等边三角形的性质可得的半径,进而可得出结论.
本题考查正多边形和圆的关系.
10.【答案】
【解析】根据题意,得图中的黄金三角形有,,,,,,,,,,,,,,,,,,,,共个故选D.
11.【答案】
【解析】解:如图:连接,,,
多边形是正六边形,
,
,
.
故选:.
连接,,,由正六边形的性质得出,由圆周角定理即可求解.
本题考查了正六边形的性质、圆周角定理;熟练掌握正六边形的性质,由圆周角定理求出是解决问题的关键.
12.【答案】
【解析】解:连接,,
五边形是的内接正五边形,
,,,故B错误;
,
,
,
,故A错误;
,
,
,
是的切线,
,
,故D错误;
,故C正确;
故选:.
连接,,根据正五边形的性质得到,,,故B错误;求得,根据三角形的三边关系得到,故A错误;根据切线的性质得到,求得,故D错误;根据三角形的内角和定理得到,故C正确.
本题考查了正多边形与圆,等腰三角形的性质,切线的性质,正确地作出辅助线是解题的关键.
13.【答案】
【解析】如图,连接、,
在正八边形中,可得于点,于点.
正八边形每个内角为,
,
.
设,
则,
,
14.【答案】
【解析】如图,连接、、,作于点四边形是正方形,
,,
是直径,,.
,.
是等边三角形,,
在中,,,
,,.
15.【答案】
【解析】设正六边形的边长为,正六边形的每个内角,,,,,,如图,过点作于点,则,,,,
,
,,,
,,故答案为.
16.【答案】
【解析】【试题解析】
【分析】
本题考查了正多边形和圆、正六边形的性质、正十边形的性质;根据题意求出中心角的度数是解题的关键.
根据中心角的度数边数,列式计算分别求出,的度数,则,则边数中心角.
【解答】
解:连接,
是内接正六边形的一边,
,
是内接正十边形的一边,
,
,
;
故答案为:.
17.【答案】解:设这个多边形的边数为,
一个正多边形中,一个内角是与它相邻的一个外角的倍,
正多边形的内角和是外角和的倍,
,
解得,
答:这个多边形的边数是;
,
答:这个多边形的每一个外角的度数为.
【解析】设这个多边形的边数为,一个正多边形中,一个内角是与它相邻的一个外角的倍,则正多边形的内角和是外角和的倍,据此列方程即可求解;
根据正多边形的外角都相等进行求解即可.
此题考查了正多边形的外角与内角问题,熟练掌握正多边形的性质是解题的关键.
18.【答案】解:;;
,
;
正六边形.
【解析】解:正三角形时,边长,底边的高为:
;
正方形时,边长,
;
正六边形时,边长,
;
故答案为:、;;;
;
当面积一定时,耗材最少的图形是正六边形,
故答案为:正六边形.
根据周长的定义求出各图形的边长:为正三角形时,根据正三角形的性质求出高,再利用三角形的面积公式列式计算即可得解;根据正方形的面积公式列式计算即可得解;根据正六边形的面积等于个全等的等边三角形的面积的和列式计算即可得解;
根据的数据比较即可;
根据中的计算结果即可得到结论.
本题考查了正方形的性质,等边三角形的性质,正多边形,主要利用了等边三角形和正方形的面积的求解.
19.【答案】解:如图所示,
如图,正六边形即为所求;
如图,正八边形即为所求.
【解析】【分析】
此题考查的是格点作图,掌握圆的内接正六边形和内接正八边形的性质和中心角的求法是解决此题的关键.
设的延长线与圆交于点,根据正六边形的性质,点即为正六边形的一个顶点,且正六边形的边长等于圆的半径,根据垂直平分线的性质即可确定其它顶点;
先求出圆内接八边形的中心角,然后根据正方形的性质即可找到各个顶点.
【解答】
解:设的延长线与圆交于点,
根据圆的内接正六边形的性质,点即为正六边形的一个顶点,且正六边形的边长等于圆的半径,即,故在图中找到的中垂线与圆的交点即为正六边形的顶点和;同理:在图中找到的中垂线与圆的交点即为正六边形的顶点和,连接、、、、、,如图,正六边形即为所求.
圆的内接八边形的中心角为,而正方形的对角线与边的夹角也为
在如图所示的正方形中,连接对角线并延长,交圆于点,此时;,
的延长线与圆的交点即为点.
同理,即可确定点、、、、的位置,顺次连接,
如图,正八边形即为所求.
20.【答案】解:任务:设桃形李产量的年平均增长率为,
由题意得:
,
解得:,不符合题意,舍去,
答:桃形李产量的年平均增长率为;
任务:设裁掉正方形的边长为,由题意得:
,
化简得,,
整理得,,
解得:,不符合题意舍去,
答:此时纸盒的高为;
任务:如图,设底面正六边形为,连接、、,和交于点,和交于点,所在直线交长方形纸板的边于点、,
设底面正六边形的边长为,纸盒的高为,
正六边形的每条边相等,每个内角都为,
为等腰三角形,,
,
由正六边形的性质可得平分,
,
,
直角三角形中,,,
同理可得直角三角形中,,
,,
,
左侧小三角形顶点的角度,
左侧小三角形为边长的等边三角形,
根据图形的上下对称可得与长方形纸板的左右两边垂直,
为等边三角形的高,
,
同理可得,
四边形为矩形,
,
,
,
联立式可得,
答:纸盒的高为;
【解析】任务:设桃形李产量的年平均增长率为,则年的产量为千克,由年的产量解方程即可;
任务:由图可得裁掉正方形的边长即为图长方体盒子的高,设裁掉正方形的边长为,根据长方体纸盒的底面积列方程求解即可;
任务:设底面正六边形为,连接、、,和交于点,和交于点,所在直线交长方形纸板的边于点、,根据正六边形的性质求得为含角的直角三角形,可得其两直角边的长度;结合等边三角形的判定和性质再求得左右两侧小三角形的高,然后根据长方形纸板的长和宽建立方程求解即可.
本题考查了一元二次方程的应用,正六边形的性质,等边三角形的判定和性质,角的直角三角形的边长关系,对称的性质;掌握正六边形的性质是解题关键.
21.【答案】解:如图即为所求.
若正六边形边长为,
连接,
点为六边形中心,
,
又,
为等边三角形,
即,
设半径为,
则,,
中,,
,
则,
由勾股定理得:,
,
,
即,,
.
【解析】本题考查切线的判定与性质和正多边形的计算关系,掌握等边三角形的性质是解题的关键。
第步:分别以点、为圆心,大于长为半径画圆弧,两弧分别交于,两点,连接并延长与延长线交于点此作
图方法作出中垂线,由正六边形对称性可知,必过正六边形中心点
第步:以点为圆心,任意长度为半径画圆弧,分别交于点,交于点再分别以点、为圆心大于长为半径画
圆弧,两弧交于点,作射线,即平分,
第步:连接由对称性可知,经过中心与射线与交于点,再以点为圆心,长为半径画圆,则即为所求.
设,则,由题意得,,中,根据勾股定理求解即可。
22.【答案】证明:,
,
又,
.
又、平分、.
,
.
易证五边形为正五边形.
【解析】求证五边形是正五边形,就是证明这个五边形的五条边所对的弧相等.
本题主要考查了连接圆的等分点所得到的多边形是正多边形这一结论.
23.【答案】证明:在中,
与是所对的圆周角,与是所对的圆周角,
,,
又,
,
为等边三角形;
过作于,连接,
则,,
,
,
等边的边心距为.
【解析】【分析】
本题考查了正多边形与圆,圆周角定理、等边三角形的判定与性质,正确作出辅助线,证明是等边三角形是关键.
利用圆周角定理可得,,而,所以,从而可判断的形状;
过作于,连接,根据直角三角形的性质即可得到结论.
24.【答案】证明:五边形是正五边形,
,,
在和中,
,
≌,
,
,
,
在和中,
,
≌,
.
【解析】连接和,证明≌可得,再证明≌即可得结论.
本题考查了正多边形的性质以及全等三角形的判定与性质,解决本题的关键是掌握正多边形的性质.
25.【答案】解:如图,点为的外心.
如图,正六边形即为所求.
【解析】【分析】本题考查尺规作图复杂作图,等边三角形的性质,三角形的外接圆与外心,正多边形的计算.
根据垂直平分线的作法作出,的垂直平分线交于点即为所求;
过点作交于,分别以,为圆心,长为半径作圆弧交于,交于,过点作交于,过点作交于,六边形即为所求正六边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.6正多边形与圆沪科版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1.周长相等的正方形与正六边形的面积分别为,,则和的关系为( )
A. B.
C. D.
2.个大小相同的正六边形按如图所示方式紧密排列在同一平面内,、、、、、均是正六边形的顶点,则点是下列哪个三角形的外心.( )
A. B. C. D.
3.如图,设边长为的等边三角形的高、内切圆的半径、外接圆的半径分别为、、,则下列结论不正确的是( )
A. B. C. D.
4.如图,在平面直角坐标系中,边长为的正六边形的中心与原点重台,轴,交轴于点将绕点逆时针旋转,每次旋转,则第次旋转结束时,点的坐标为( )
A.
B.
C.
D.
5.如图,已知正五边形内接于,连结,则的度数为( )
A. B. C. D.
6.半径为的圆内接正三角形、正方形、正六边形的边心距分别为,,,则,,的大小关系是( )
A. B. C. D.
7.如图,点是边长为的正六边形的中心,对角线,相交于点,则的面积为( )
A.
B.
C.
D.
8.蜂巢结构精巧,其巢房横截面的形状均为正六边形如图是部分巢房的横截面图,图中个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点,,均为正六边形的顶点若点,的坐标分别为,,则点的坐标为( )
A. B. C. D.
9.正六边形内接于,正六边形的周长是,则的半径是( )
A. B. C. D.
10.如图,点为正五边形外接圆的圆心,正五边形的对角线分别相交于点,,,,若顶角等于的等腰三角形叫做黄金三角形,那么图中黄金三角形的个数为( )
A. B. C. D.
11.如图,正六边形内接于,点在上,则的度数为( )
A.
B.
C.
D.
12.如图,五边形是的内接正五边形,过点作的切线交的延长线于点,交的延长线于点则下列结论中正确的是( )
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
13.如图,在正八边形中,若四边形的面积是,则正八边形的面积为 .
14.如图,正方形内接于,其边长为,则的内接正三角形的边长为 .
15.如图,在正六边形中,连接,,则 度.
16.如图,是的内接正六边形的一边,点在上,且是的内接正十边形的一边,若是的内接正边形的一边,则____.
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
在一个正多边形中,一个内角是与它相邻的一个外角的倍.
求这个多边形的边数;
求这个多边形的每一个外角的度数.
18.本小题分
自古以来,人类对于蜜蜂的勤劳以及蜂巢的巧妙精准无不赞扬有加.从生物学鼻祖亚里士多德,到数学家帕普斯,以及近代的生物学家达尔文都曾留下了赞美的诗句.工蜂分泌蜂蜡筑成蜂窝,作为蜂王产卵、工蜂育幼以及存放蜂蜜、花粉的贮藏室.从正面来看,蜂巢是由许多正六边形连结而成,正六边形是能够不重叠地铺满一个平面的三种正多边形之一,另外两种分别是正方形和正三角形.
一根长的铁丝分别围成正三角形,正方形,正六边形,请同学们直接写出围成图形的面积:______,______,______;
在的条件下,比较围成图形面积的大小;
通过以上计算,当面积一定时,耗材最少的图形是______填:正三角形、正方形、正六边形.
19.本小题分
如图,在网格纸中,、都是格点,以为圆心,为半径作圆.用无刻度的直尺完成以下画图:不写画法
在图中画的一个内接正六边形;
在图中画的一个内接正八边形.
20.本小题分
浦江桃形李是地方名果,是浦江县的特产之一请你运用数学知识,根据素材,帮果农解决问题.
信息及素材
素材一 在专业种植技术人员的正确指导下,果农对桃形李的种植技术进行了研究与改进,使产量得到了增长,根据果农们的记录,年桃形李平均每株产量是千克,年达到了千克,每年的增长率是相同的.
素材二 一般采用的是长方体包装盒.
素材三 果农们通过问卷调查发现,顾客也很愿意购买美观漂亮的其它设计的包装纸盒.
任务:求桃形李产量的年平均增长率;
任务:现有长,宽的长方形纸板,将四角各裁掉一个正方形如图,折成无盖长方体纸盒如图为了放下适当数量的桃形李,需要设计底面积为的纸盒,计算此时纸盒的高;
任务:为了增加包装盒的种类,打算将任务中的纸板通过图的方式裁剪,得到底面为正六边形的无盖纸盒如图,求出此时纸盒的高图中实线表示剪切线,虚线表示折痕纸板厚度及剪切接缝处损耗忽略不计
21.本小题分
门环,在中国绵延了数千多年的,集实用、装饰和门第等级为一体的一种古建筑构件,也成为中国古建“门文化”中的一部分,现有一个门环的示意图如图所示,点为正六边形的中心;
请用无刻度直尺与圆规,过点作一个,使与直线和直线同时相切;请保留作图痕迹
若正六边形的边长为,试求中的半径。结果保留根号
22.本小题分
已知:如图,是的内接等腰三角形,顶角,弦、分别平分、.
求证:五边形是正五边形.
23.本小题分
如图,,,,是上的四个点,.
求证:是等边三角形.
若的半径为,求等边的边心距.
24.本小题分
如图,在正五边形中,为垂足.求证:.
25.本小题分
如图,已知等边,请用直尺不带刻度和圆规按下列要求作图不要求写作法,但要保留作图痕迹
作的外心
设是边上一点,在图中作出一个正六边形,使点、点分别在边和上.
答案和解析
1.【答案】
【解析】设正方形的边长为,则正六边形的边长为,.正六边形的边长为,把正六边形分成六个全等的小正三角形,其高为,,,故选D.
2.【答案】
【解析】本题考查了三角形外心的性质,即到三角形三个顶点的距离相等,依次判断即可.
因为三角形的外心到三角形的三个顶点的距离相等,由正六边形性质可知,点到、、、、的距离中,只有,
所以点是的外心.故选D.
3.【答案】
【解析】如图,是等边三角形,
的内切圆和外接圆是同心圆,圆心为.
设,为切点,连接,,,易得点,,共线,则,,,
,故A正确.
,
.
在中,,即,故B正确.
,,
,
,,故C错误,D正确.
故选C.
4.【答案】
【解析】解:正六边形边长为,中心与原点重合,轴,
,,
:.
第次旋转结束时,点的坐标为;
第次旋转结束时,点的坐标为;
第次旋转结束时,点的坐标为;
第次旋转结束时,点的坐标为.,
次一个循环,
.
第次旋转结束时,点的坐标为.
故选:.
首先确定点的坐标,再根据次一个循环,推出经过第次旋转后,点的坐标即可.
本题考查正多边形的性质,规律型问题,坐标与图形变化旋转等知识,解题的关键是学会探究规律的方法,属于中考常考题型.
5.【答案】
【解析】略
6.【答案】
【解析】【分析】
此题主要考查了正多边形和圆的性质,解决本题的关键是构造直角三角形,得到用半径表示的边心距;注意:正多边形的计算一般要转化为解直角三角形的问题来解决.
根据三角函数即可求解.
【解答】
解:设圆的半径为,
则正三角形的边心距为
正方形的边心距为,
正六边形的边心距为
,
,
故选:.
7.【答案】
【解析】解:六边形是边长为的正六边形,
,,
,
,
,
,
的面积.
故选:.
根据六边形是边长为的正六边形,可得,,根据三角形内角和定理可得,所以,然后利用含度角的直角三角形可得的长,进而可以解决问题.
本题考查了正多边形和三角形的面积,解决本题的关键是掌握正六边形的性质.
8.【答案】
【解析】解:设中间正六边形的中心为,连接.
点,的坐标分别为,,图中是个全等的正六边形,
,,
,
,
,
,,
,
故选:.
设中间正六边形的中心为,连接判断出,的长,可得结论.
本题考查正多边形与圆,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
9.【答案】
【解析】解:连接,,
多边形是正六边形,
,
,
是等边三角形,
,
正六边形的周长是,
,
的半径是,
故选B.
连接,,根据等边三角形的性质可得的半径,进而可得出结论.
本题考查正多边形和圆的关系.
10.【答案】
【解析】根据题意,得图中的黄金三角形有,,,,,,,,,,,,,,,,,,,,共个故选D.
11.【答案】
【解析】解:如图:连接,,,
多边形是正六边形,
,
,
.
故选:.
连接,,,由正六边形的性质得出,由圆周角定理即可求解.
本题考查了正六边形的性质、圆周角定理;熟练掌握正六边形的性质,由圆周角定理求出是解决问题的关键.
12.【答案】
【解析】解:连接,,
五边形是的内接正五边形,
,,,故B错误;
,
,
,
,故A错误;
,
,
,
是的切线,
,
,故D错误;
,故C正确;
故选:.
连接,,根据正五边形的性质得到,,,故B错误;求得,根据三角形的三边关系得到,故A错误;根据切线的性质得到,求得,故D错误;根据三角形的内角和定理得到,故C正确.
本题考查了正多边形与圆,等腰三角形的性质,切线的性质,正确地作出辅助线是解题的关键.
13.【答案】
【解析】如图,连接、,
在正八边形中,可得于点,于点.
正八边形每个内角为,
,
.
设,
则,
,
14.【答案】
【解析】如图,连接、、,作于点四边形是正方形,
,,
是直径,,.
,.
是等边三角形,,
在中,,,
,,.
15.【答案】
【解析】设正六边形的边长为,正六边形的每个内角,,,,,,如图,过点作于点,则,,,,
,
,,,
,,故答案为.
16.【答案】
【解析】【试题解析】
【分析】
本题考查了正多边形和圆、正六边形的性质、正十边形的性质;根据题意求出中心角的度数是解题的关键.
根据中心角的度数边数,列式计算分别求出,的度数,则,则边数中心角.
【解答】
解:连接,
是内接正六边形的一边,
,
是内接正十边形的一边,
,
,
;
故答案为:.
17.【答案】解:设这个多边形的边数为,
一个正多边形中,一个内角是与它相邻的一个外角的倍,
正多边形的内角和是外角和的倍,
,
解得,
答:这个多边形的边数是;
,
答:这个多边形的每一个外角的度数为.
【解析】设这个多边形的边数为,一个正多边形中,一个内角是与它相邻的一个外角的倍,则正多边形的内角和是外角和的倍,据此列方程即可求解;
根据正多边形的外角都相等进行求解即可.
此题考查了正多边形的外角与内角问题,熟练掌握正多边形的性质是解题的关键.
18.【答案】解:;;
,
;
正六边形.
【解析】解:正三角形时,边长,底边的高为:
;
正方形时,边长,
;
正六边形时,边长,
;
故答案为:、;;;
;
当面积一定时,耗材最少的图形是正六边形,
故答案为:正六边形.
根据周长的定义求出各图形的边长:为正三角形时,根据正三角形的性质求出高,再利用三角形的面积公式列式计算即可得解;根据正方形的面积公式列式计算即可得解;根据正六边形的面积等于个全等的等边三角形的面积的和列式计算即可得解;
根据的数据比较即可;
根据中的计算结果即可得到结论.
本题考查了正方形的性质,等边三角形的性质,正多边形,主要利用了等边三角形和正方形的面积的求解.
19.【答案】解:如图所示,
如图,正六边形即为所求;
如图,正八边形即为所求.
【解析】【分析】
此题考查的是格点作图,掌握圆的内接正六边形和内接正八边形的性质和中心角的求法是解决此题的关键.
设的延长线与圆交于点,根据正六边形的性质,点即为正六边形的一个顶点,且正六边形的边长等于圆的半径,根据垂直平分线的性质即可确定其它顶点;
先求出圆内接八边形的中心角,然后根据正方形的性质即可找到各个顶点.
【解答】
解:设的延长线与圆交于点,
根据圆的内接正六边形的性质,点即为正六边形的一个顶点,且正六边形的边长等于圆的半径,即,故在图中找到的中垂线与圆的交点即为正六边形的顶点和;同理:在图中找到的中垂线与圆的交点即为正六边形的顶点和,连接、、、、、,如图,正六边形即为所求.
圆的内接八边形的中心角为,而正方形的对角线与边的夹角也为
在如图所示的正方形中,连接对角线并延长,交圆于点,此时;,
的延长线与圆的交点即为点.
同理,即可确定点、、、、的位置,顺次连接,
如图,正八边形即为所求.
20.【答案】解:任务:设桃形李产量的年平均增长率为,
由题意得:
,
解得:,不符合题意,舍去,
答:桃形李产量的年平均增长率为;
任务:设裁掉正方形的边长为,由题意得:
,
化简得,,
整理得,,
解得:,不符合题意舍去,
答:此时纸盒的高为;
任务:如图,设底面正六边形为,连接、、,和交于点,和交于点,所在直线交长方形纸板的边于点、,
设底面正六边形的边长为,纸盒的高为,
正六边形的每条边相等,每个内角都为,
为等腰三角形,,
,
由正六边形的性质可得平分,
,
,
直角三角形中,,,
同理可得直角三角形中,,
,,
,
左侧小三角形顶点的角度,
左侧小三角形为边长的等边三角形,
根据图形的上下对称可得与长方形纸板的左右两边垂直,
为等边三角形的高,
,
同理可得,
四边形为矩形,
,
,
,
联立式可得,
答:纸盒的高为;
【解析】任务:设桃形李产量的年平均增长率为,则年的产量为千克,由年的产量解方程即可;
任务:由图可得裁掉正方形的边长即为图长方体盒子的高,设裁掉正方形的边长为,根据长方体纸盒的底面积列方程求解即可;
任务:设底面正六边形为,连接、、,和交于点,和交于点,所在直线交长方形纸板的边于点、,根据正六边形的性质求得为含角的直角三角形,可得其两直角边的长度;结合等边三角形的判定和性质再求得左右两侧小三角形的高,然后根据长方形纸板的长和宽建立方程求解即可.
本题考查了一元二次方程的应用,正六边形的性质,等边三角形的判定和性质,角的直角三角形的边长关系,对称的性质;掌握正六边形的性质是解题关键.
21.【答案】解:如图即为所求.
若正六边形边长为,
连接,
点为六边形中心,
,
又,
为等边三角形,
即,
设半径为,
则,,
中,,
,
则,
由勾股定理得:,
,
,
即,,
.
【解析】本题考查切线的判定与性质和正多边形的计算关系,掌握等边三角形的性质是解题的关键。
第步:分别以点、为圆心,大于长为半径画圆弧,两弧分别交于,两点,连接并延长与延长线交于点此作
图方法作出中垂线,由正六边形对称性可知,必过正六边形中心点
第步:以点为圆心,任意长度为半径画圆弧,分别交于点,交于点再分别以点、为圆心大于长为半径画
圆弧,两弧交于点,作射线,即平分,
第步:连接由对称性可知,经过中心与射线与交于点,再以点为圆心,长为半径画圆,则即为所求.
设,则,由题意得,,中,根据勾股定理求解即可。
22.【答案】证明:,
,
又,
.
又、平分、.
,
.
易证五边形为正五边形.
【解析】求证五边形是正五边形,就是证明这个五边形的五条边所对的弧相等.
本题主要考查了连接圆的等分点所得到的多边形是正多边形这一结论.
23.【答案】证明:在中,
与是所对的圆周角,与是所对的圆周角,
,,
又,
,
为等边三角形;
过作于,连接,
则,,
,
,
等边的边心距为.
【解析】【分析】
本题考查了正多边形与圆,圆周角定理、等边三角形的判定与性质,正确作出辅助线,证明是等边三角形是关键.
利用圆周角定理可得,,而,所以,从而可判断的形状;
过作于,连接,根据直角三角形的性质即可得到结论.
24.【答案】证明:五边形是正五边形,
,,
在和中,
,
≌,
,
,
,
在和中,
,
≌,
.
【解析】连接和,证明≌可得,再证明≌即可得结论.
本题考查了正多边形的性质以及全等三角形的判定与性质,解决本题的关键是掌握正多边形的性质.
25.【答案】解:如图,点为的外心.
如图,正六边形即为所求.
【解析】【分析】本题考查尺规作图复杂作图,等边三角形的性质,三角形的外接圆与外心,正多边形的计算.
根据垂直平分线的作法作出,的垂直平分线交于点即为所求;
过点作交于,分别以,为圆心,长为半径作圆弧交于,交于,过点作交于,过点作交于,六边形即为所求正六边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
