6.4三角形中位线定理学案

6.4三角形中位线定理
1、怎样将一张三角形纸片剪成两部分，使分成的两部分能拼与一个平行四边形。
2、三角形中位线及三角形中位线定理
（1）．三角形中位线定义： 叫做三角形的中位线。
（2）：三角形中位线定理 。
创设情境：
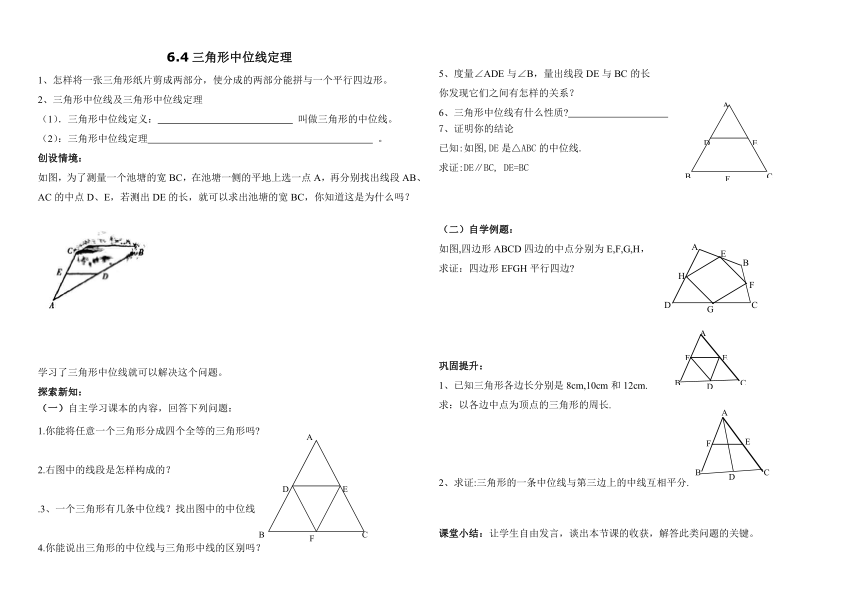
如图，为了测量一个池塘的宽BC，在池塘一侧的平地上选一点A，再分别找出线段AB、AC的中点D、E，若测出DE的长，就可以求出池塘的宽BC，你知道这是为什么吗？
学习了三角形中位线就可以解决这个问题。
探索新知：
（一）自主学习课本的内容，回答下列问题：
1.你能将任意一个三角形分成四个全等的三角形吗
2.右图中的线段是怎样构成的？
.3、一个三角形有几条中位线？找出图中的中位线
4.你能说出三角形的中位线与三角形中线的区别吗？
5、度量∠ADE与∠B，量出线段DE与BC的长
你发现它们之间有怎样的关系？
6、三角形中位线有什么性质
7、证明你的结论
已知:如图,DE是△ABC的中位线.
求证:DE∥BC, DE=BC
（二）自学例题：
如图,四边形ABCD四边的中点分别为E,F,G,H，
求证：四边形EFGH平行四边
巩固提升：
1、已知三角形各边长分别是8cm,10cm和12cm.
求：以各边中点为顶点的三角形的周长.
2、求证:三角形的一条中位线与第三边上的中线互相平分.
课堂小结：让学生自由发言，谈出本节课的收获，解答此类问题的关键。
达标检测： (学生独立完成)
如图；三角形三条中位线组成的图形与原三角形有怎样的大小关系（面积和周长）？ 说说你的理由。
已知：在四边形ABCD中，AB=CD，E、F、G分别是BD、AC、BC的中点。
求证：⊿EFG是等腰三角形。
3、已知:如图,在四边形ABCD中,E,F,G,H分别是
边AB,CD,AC,BD的中点.
求证:四边形EGFH是平行四边形
C
A
B
D
E
F
C
A
B
D
E
F
A
B
C
H
D
E
F
G
C
D
A
F
B
E
A
E
F
B
C
D
H
E
G
A
D
F
C
B