人教版六年级数学上册《圆的面积》(课件)(共26张PPT)
文档属性
| 名称 | 人教版六年级数学上册《圆的面积》(课件)(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 10:52:15 | ||
图片预览




文档简介
(共26张PPT)
圆的面积
(第一课时)
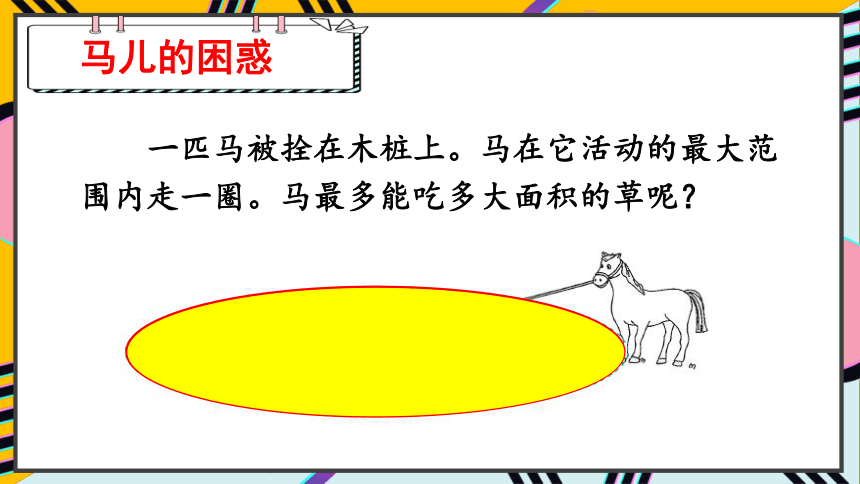
一匹马被拴在木桩上。马在它活动的最大范围内走一圈。马最多能吃多大面积的草呢?
马儿的困惑
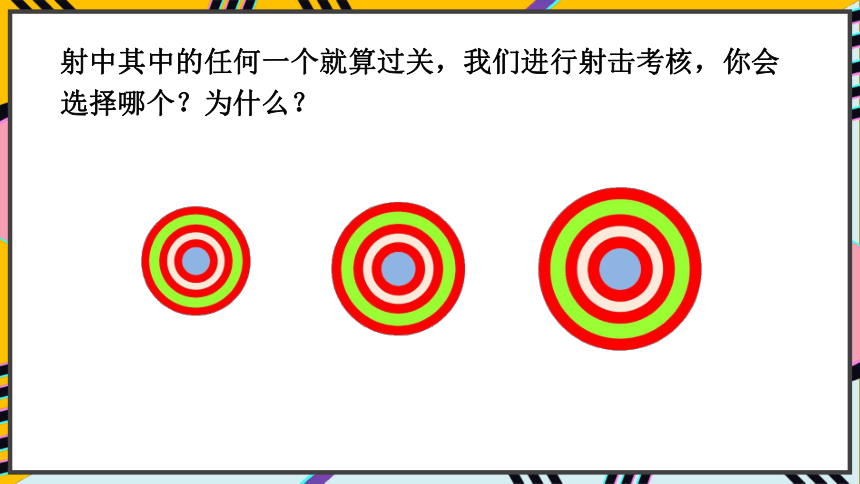
射中其中的任何一个就算过关,我们进行射击考核,你会选择哪个?为什么?
圆的大小和什么有关系?
R
r
半径r决定圆的大小
什么是圆的面积呢
圆所占平面的大小叫做圆的面积。
圆,是( )图形
平面
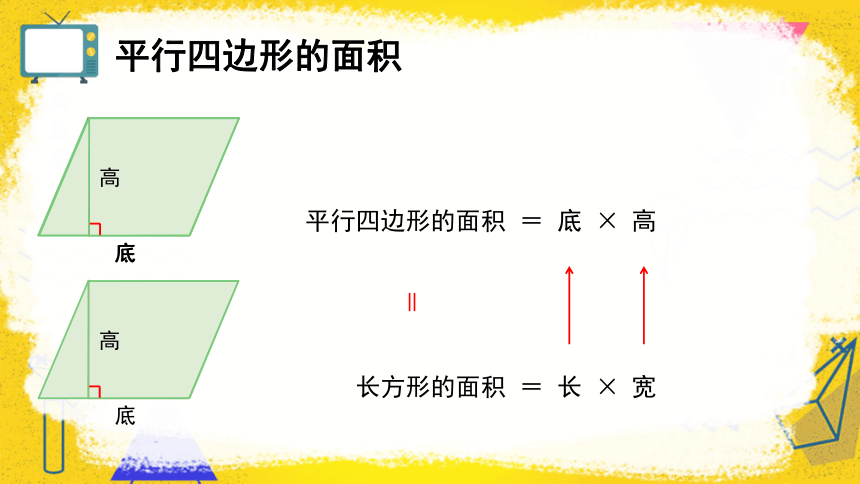
平行四边形的面积
=
长
×
宽
高
底
高
底
长方形的面积
平行四边形的面积
=
底
×
高
高
底
=
=
底
×
高
平行四边形的面积
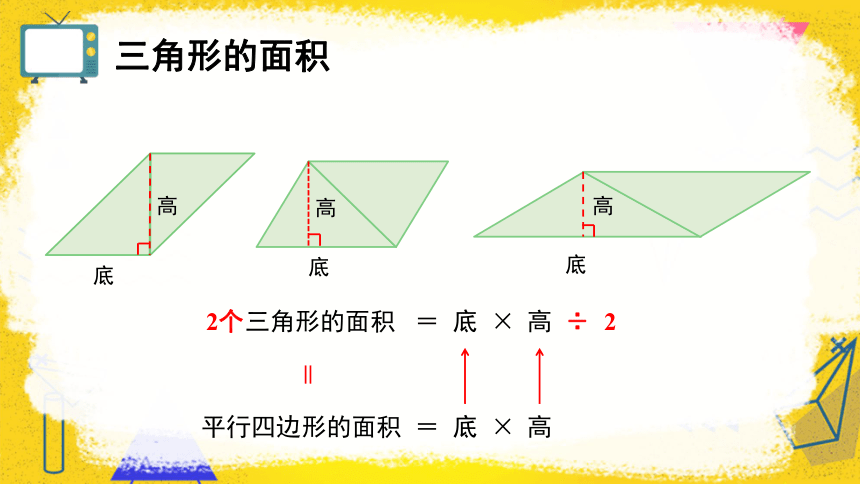
三角形的面积
=
底
×
高
=
2个
÷
2
底
底
底
高
高
高
三角形的面积
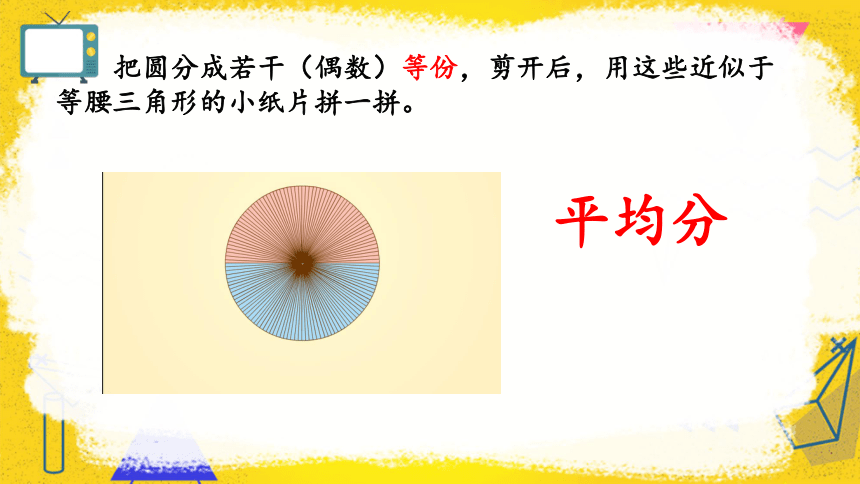
把圆分成若干(偶数)等份,剪开后,用这些近似于等腰三角形的小纸片拼一拼。
平均分
1
2
3
4
1
2
3
4
1
2
3
4
5
6
7
8
1
2
3
4
2
3
1
4
6
7
5
8
2
3
1
4
6
7
5
8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
观察下列拼成的图形,你有什么发现?
4
圆的面积公式
圆
近似的长方形
圆的半径 = 长方形的宽
割补转化
面积相等
长
半径
r
宽
宽
圆周长的一半 = 长方形的长
长方形的面积 = 长 × 宽
长
圆的面积 = 圆周长的一半 × 半径
S = πr × r = πr2
S=πr2
要求出圆的面积,必须知道什么条件?
一般π取3.14
马儿的最大活动范围有多大?
绳子的长度为10米
S = πr2
=3.14×102
=3.14×10×10
=314(平方米)
答:马儿的最大活动范围是314平方米。
运用公式,解决问题
水牛兄弟的绳子是我的绳子长度的一半,他的活动范围是多少呢?
我的绳长为10米
答:水牛的活动范围是78.5平方米。
运用公式,解决问题
“一半” r =10 ÷2=5 (m)
S = πr2
=3.14×52
=3.14×5×5
=78.5(平方米)
答对,进入下一关
答题挑战
巩固练习
1.把一根长25.12米的铁丝围成一个圆,这个圆的面积多少平方米?
S = πr2
= 3.14×4
= 50.24(m )
答:这个圆的面积是50.24平方米。
C=2πr
C=πd
C = 25.12÷3.14÷2=4(m)
2.一个钟表,时针长8厘米,它一昼夜扫过多少平方厘米?
r = 8(cm)
S = πr2
= 3.14×82
= 3.14×8 ×8
= 3.14 ×64
= 200.96(m2)
一昼夜: 200.96×2=401.92(m2)
答:它的面积是401.92平方米。
巩固练习
恭喜过关!
数学方法和数学思想:
都是通过( )的方法,将要学习
的新图形( )成( )
来推导新图形的面积计算公式。在转换的过程中( )
没变,( )发生改变。
把( )转换成( )。
剪、移、拼
转化
已经学过的图形
面积
形状
新知识
旧知识
课堂收获
1.分的份数(偶数)越多,拼成的图形越接近长方形
2. 长方形的长 = 圆周长的一半( πr )
长方形的宽 = 圆的半径( r )
长方形的面积 = πr2 = 圆的面积
S=πr2 一般π取3.14
利用旧知识,学习新知识。
布置作业
1.练习十五的第1—4题;
2.数学作业本27页。
人的知识就像一个圆,
圆内是已知,圆外是未知。
你知道的越多,
你的圆圈就会越大,
圆的周长也会越大,
你与未知接触的空间也越大。
你知道的东西越多,
不知道的东西也会越多。
——古希腊哲学家 芝诺
谢谢!
圆的面积
(第一课时)
一匹马被拴在木桩上。马在它活动的最大范围内走一圈。马最多能吃多大面积的草呢?
马儿的困惑
射中其中的任何一个就算过关,我们进行射击考核,你会选择哪个?为什么?
圆的大小和什么有关系?
R
r
半径r决定圆的大小
什么是圆的面积呢
圆所占平面的大小叫做圆的面积。
圆,是( )图形
平面
平行四边形的面积
=
长
×
宽
高
底
高
底
长方形的面积
平行四边形的面积
=
底
×
高
高
底
=
=
底
×
高
平行四边形的面积
三角形的面积
=
底
×
高
=
2个
÷
2
底
底
底
高
高
高
三角形的面积
把圆分成若干(偶数)等份,剪开后,用这些近似于等腰三角形的小纸片拼一拼。
平均分
1
2
3
4
1
2
3
4
1
2
3
4
5
6
7
8
1
2
3
4
2
3
1
4
6
7
5
8
2
3
1
4
6
7
5
8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
观察下列拼成的图形,你有什么发现?
4
圆的面积公式
圆
近似的长方形
圆的半径 = 长方形的宽
割补转化
面积相等
长
半径
r
宽
宽
圆周长的一半 = 长方形的长
长方形的面积 = 长 × 宽
长
圆的面积 = 圆周长的一半 × 半径
S = πr × r = πr2
S=πr2
要求出圆的面积,必须知道什么条件?
一般π取3.14
马儿的最大活动范围有多大?
绳子的长度为10米
S = πr2
=3.14×102
=3.14×10×10
=314(平方米)
答:马儿的最大活动范围是314平方米。
运用公式,解决问题
水牛兄弟的绳子是我的绳子长度的一半,他的活动范围是多少呢?
我的绳长为10米
答:水牛的活动范围是78.5平方米。
运用公式,解决问题
“一半” r =10 ÷2=5 (m)
S = πr2
=3.14×52
=3.14×5×5
=78.5(平方米)
答对,进入下一关
答题挑战
巩固练习
1.把一根长25.12米的铁丝围成一个圆,这个圆的面积多少平方米?
S = πr2
= 3.14×4
= 50.24(m )
答:这个圆的面积是50.24平方米。
C=2πr
C=πd
C = 25.12÷3.14÷2=4(m)
2.一个钟表,时针长8厘米,它一昼夜扫过多少平方厘米?
r = 8(cm)
S = πr2
= 3.14×82
= 3.14×8 ×8
= 3.14 ×64
= 200.96(m2)
一昼夜: 200.96×2=401.92(m2)
答:它的面积是401.92平方米。
巩固练习
恭喜过关!
数学方法和数学思想:
都是通过( )的方法,将要学习
的新图形( )成( )
来推导新图形的面积计算公式。在转换的过程中( )
没变,( )发生改变。
把( )转换成( )。
剪、移、拼
转化
已经学过的图形
面积
形状
新知识
旧知识
课堂收获
1.分的份数(偶数)越多,拼成的图形越接近长方形
2. 长方形的长 = 圆周长的一半( πr )
长方形的宽 = 圆的半径( r )
长方形的面积 = πr2 = 圆的面积
S=πr2 一般π取3.14
利用旧知识,学习新知识。
布置作业
1.练习十五的第1—4题;
2.数学作业本27页。
人的知识就像一个圆,
圆内是已知,圆外是未知。
你知道的越多,
你的圆圈就会越大,
圆的周长也会越大,
你与未知接触的空间也越大。
你知道的东西越多,
不知道的东西也会越多。
——古希腊哲学家 芝诺
谢谢!
