24.4 弧长和扇形面积 同步练习(无答案)-2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.4 弧长和扇形面积 同步练习(无答案)-2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 246.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 22:01:55 | ||
图片预览

文档简介
24.4 弧长和扇形面积 同步练习-2023-2024学年人教版数学九年级上册
一、单选题
1.已知圆的半径为3,扇形的圆心角为 ,则扇形的面积为 ( )
A. B. C. D.
2.已知扇形的半径为6,圆心角为,则扇形的面积为( )
A. B. C. D.
3.如图,一个圆形飞镖板被分为四个圆心角相等的扇形,若大圆半径为2,小圆半径为1,则阴影部分的面积为( )
A.π B. π C.3π D. π
4.若一个扇形的半径是 ,且它的弧长是 ,则此扇形的圆心角等于( )
A. B. C. D.
5.如图,把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A、B,且O1A⊥O2A,则图中阴影部分的面积是( )
A.4π﹣8 B.16π﹣16 C.16π﹣32 D.8π﹣16
6.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则S阴影=( )
A.π B.2π C. D. π
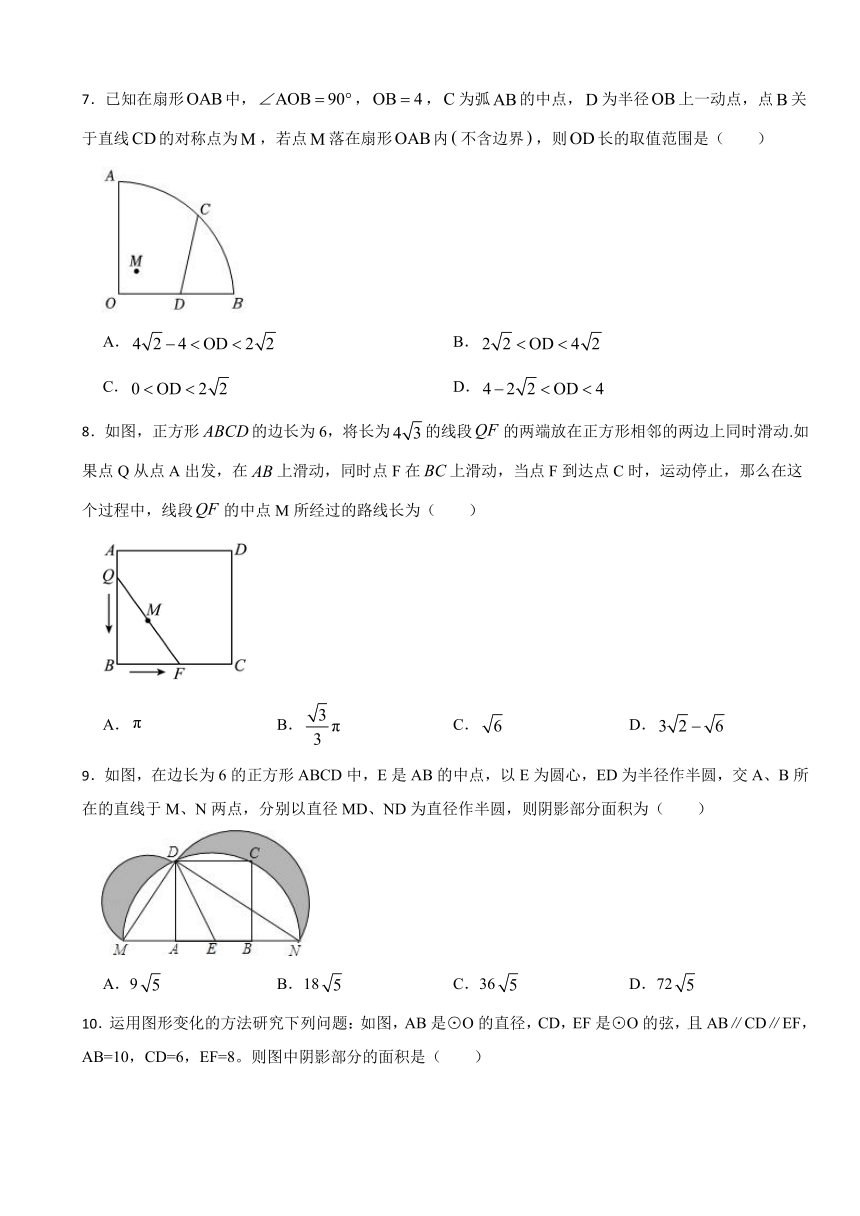
7.已知在扇形中,,,为弧的中点,为半径上一动点,点关于直线的对称点为,若点落在扇形内不含边界,则长的取值范围是( )
A. B.
C. D.
8.如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( )
A. B. C. D.
9.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
A.9 B.18 C.36 D.72
10.运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。则图中阴影部分的面积是( )
A. B. C. D.
二、填空题
11.圆心角是60°且半径为2的扇形面积是
12.一个扇形的半径为3cm,面积为π cm2,则此扇形的圆心角为 度
13.如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为 cm2.
14.如图,在矩形ABCD中,AD=4,DC=3,将△ADC绕点A按逆时针方向旋转到△AEF(点A、B、E在同一直线上),则AC在运动过程中所扫过的面积为 .
15.如图,半径为4cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设 的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为 .
三、解答题
16.如图, 是 的直径, 是 的弦,C为 延长线上的点, .
(1)求证: 是 的切线.
(2)若 的半径为6,求 的长.(结果保留 )
17.如图,在中,,平分,交于点,点在上,经过、两点,交于点,交于点.
(1)求证:是的切线;
(2)若的半径是,是的中点,求阴影部分的面积结果保留和根号
18.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点)
(1)先将△ABC竖直向上平移5个单位,再水平向右平移4个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)求线段B1C1变换到B1C2的过程中扫过区域的面积.
19.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,求图中阴影部分的面积.
20.如图,四边形ABCD是一个正方形,E,D,A,F四点在一直线上,且ED=DA=AF=2厘米,阴影部分的面积是多少平方厘米?(π取3.14)
21.如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14, ≈1.73,结果保留一位小数.)
一、单选题
1.已知圆的半径为3,扇形的圆心角为 ,则扇形的面积为 ( )
A. B. C. D.
2.已知扇形的半径为6,圆心角为,则扇形的面积为( )
A. B. C. D.
3.如图,一个圆形飞镖板被分为四个圆心角相等的扇形,若大圆半径为2,小圆半径为1,则阴影部分的面积为( )
A.π B. π C.3π D. π
4.若一个扇形的半径是 ,且它的弧长是 ,则此扇形的圆心角等于( )
A. B. C. D.
5.如图,把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A、B,且O1A⊥O2A,则图中阴影部分的面积是( )
A.4π﹣8 B.16π﹣16 C.16π﹣32 D.8π﹣16
6.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则S阴影=( )
A.π B.2π C. D. π
7.已知在扇形中,,,为弧的中点,为半径上一动点,点关于直线的对称点为,若点落在扇形内不含边界,则长的取值范围是( )
A. B.
C. D.
8.如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( )
A. B. C. D.
9.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
A.9 B.18 C.36 D.72
10.运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。则图中阴影部分的面积是( )
A. B. C. D.
二、填空题
11.圆心角是60°且半径为2的扇形面积是
12.一个扇形的半径为3cm,面积为π cm2,则此扇形的圆心角为 度
13.如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为 cm2.
14.如图,在矩形ABCD中,AD=4,DC=3,将△ADC绕点A按逆时针方向旋转到△AEF(点A、B、E在同一直线上),则AC在运动过程中所扫过的面积为 .
15.如图,半径为4cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设 的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为 .
三、解答题
16.如图, 是 的直径, 是 的弦,C为 延长线上的点, .
(1)求证: 是 的切线.
(2)若 的半径为6,求 的长.(结果保留 )
17.如图,在中,,平分,交于点,点在上,经过、两点,交于点,交于点.
(1)求证:是的切线;
(2)若的半径是,是的中点,求阴影部分的面积结果保留和根号
18.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点)
(1)先将△ABC竖直向上平移5个单位,再水平向右平移4个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)求线段B1C1变换到B1C2的过程中扫过区域的面积.
19.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,求图中阴影部分的面积.
20.如图,四边形ABCD是一个正方形,E,D,A,F四点在一直线上,且ED=DA=AF=2厘米,阴影部分的面积是多少平方厘米?(π取3.14)
21.如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14, ≈1.73,结果保留一位小数.)
同课章节目录
