第6章 反比例函数基础检测 (无答案)2023—2024学年北师大版数学九年级上册
文档属性
| 名称 | 第6章 反比例函数基础检测 (无答案)2023—2024学年北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 422.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 00:00:00 | ||
图片预览

文档简介
第6章 反比例函数基础检测 2023—2024学年北师大版数学九年级上册
一、单选题
1.下列函数中,y是x的反比例函数的是( )
A.x(y﹣1)=1 B.y=
C.y= D.y=
2.下列图象中是反比例函数y=﹣ 图象的是( )
A. B.
C. D.
3.一次函数y1=kx+b和反比例函数y2= 的图象如图,则使y1>y2的x范围是( )
A.x<﹣2或x>3 B.﹣2<x<0或x>3
C.x<﹣2或0<x<3 D.﹣2<x<3
4.如图,A为反比例函数y=(k>0)图象上一点,AB⊥x轴于点B,若S△AOB=3,则k的值为( )
A.1.5 B.3 C. D.6
5.如图,在平面直角坐标系中,点A在第一象限。AB⊥y轴于点B,函数y= (x>0)的图象与线段AB交于点C,且AB=3BC.若△AOB的面积为12.则k的值为( )
A.4 B.6 C.8 D.12
6.反比例函数y= 的图象上,当x<0时,y随x的增大而增大,则m的取值范围是( )
A.m>-2 B.m<0 C.m<-2 D.m>0
7.如图,直线y=-x与双曲线y= 的图象交于A、B两点,过点A作AC⊥y轴于点C,连接BC,若S△ACB=4,则k的值为( )
A.-4 B.4 C.-8 D.8
8.如图,平行四边形AOBC中,∠AOB=60°,AO=8,AC=15,反比例函数y= (x>0)图象经过点A,与BC交于点D,则 的值为( )
A. B. C. D.
9.古希腊数学家帕普斯利用反比例函数的图象和性质解决了三等分角问题,其方法如下:如图,在直角坐标系中,锐角的边OB在x轴正半轴上,边OA与的图象交于点A,以A为圆心,2OA为半径作圆弧交函数图象于点C,取AC的中点P,则.若,则k的值为( )
A. B. C. D.
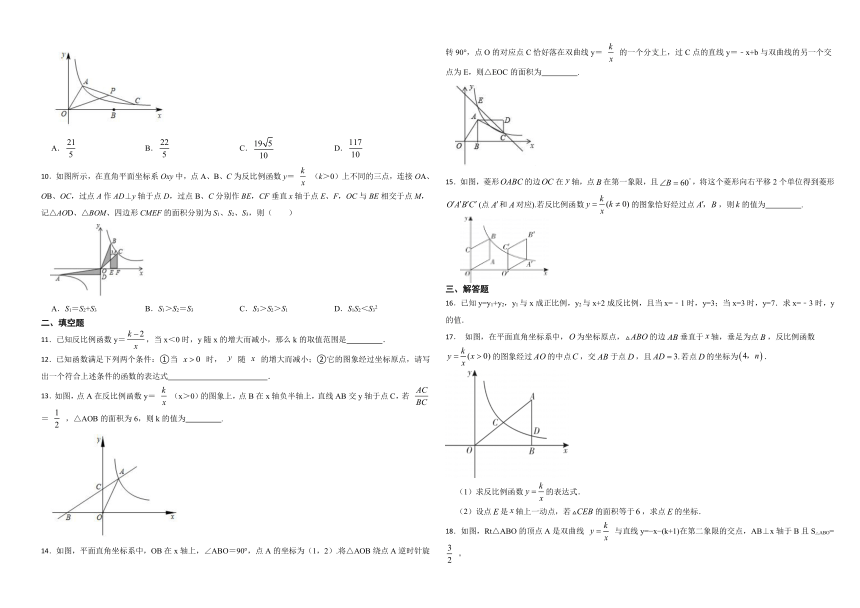
10.如图所示,在直角平面坐标系Oxy中,点A、B、C为反比例函数y= (k>0)上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则( )
A.S1=S2+S3 B.S1>S2=S3 C.S3>S2>S1 D.S1S2<S32
二、填空题
11.已知反比例函数y=,当x<0时,y随x的增大而减小,那么k的取值范围是 .
12.已知函数满足下列两个条件:①当 时, 随 的增大而减小;②它的图象经过坐标原点,请写出一个符合上述条件的函数的表达式 .
13.如图,点A在反比例函数y= (x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若 = ,△AOB的面积为6,则k的值为 .
14.如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y= 的一个分支上,过C点的直线y=﹣x+b与双曲线的另一个交点为E,则△EOC的面积为 .
15.如图,菱形的边在轴,点在第一象限,且,将这个菱形向右平移2个单位得到菱形(点和对应).若反比例函数的图象恰好经过点,则的值为 .
三、解答题
16.已知y=y1+y2,y1与x成正比例,y2与x+2成反比例,且当x=﹣1时,y=3;当x=3时,y=7.求x=﹣3时,y的值.
17. 如图,在平面直角坐标系中,为坐标原点,的边垂直于轴,垂足为点,反比例函数的图象经过的中点,交于点,且若点的坐标为.
(1)求反比例函数的表达式.
(2)设点是轴上一动点,若的面积等于,求点的坐标.
18.如图,Rt△ABO的顶点A是双曲线 与直线y= x (k+1)在第二象限的交点,AB⊥x轴于B且S△ABO= 。
(1)求这两个函数的解析式。
(2)求直线与双曲线的两个交点A,C的坐标和△AOC的面积。
19.如图所示,已知一次函数y=kx+b(k≠0)的图象与反比例函数y= 的图象交于A、B两点,且点A的横坐标和B点的纵坐标都是﹣2,求△AOB的面积.
20. 如图,已知反比例数的图象与一次函数的图象相交于点,,过点作轴于点,过点作轴于点,连结.
(1)求反比例函数和一次函数的解析式;
(2)观察图象,直接写出一次函数值大于反比例函数值时自变量的取值范围;
(3)求四边形的面积.
21.如图,△PAB的直角顶点P在第四象限,顶点A、B分别落在反比例函数 图象的两个分支上,且PB⊥x轴于点C,PA⊥y轴于点D,AB分别与x轴,y轴相交于点E、F已知B(1,3)
(1)k= ;
(2)试说明AE=BF;
(3)当四边形ABCD的面积为 时,求点P的坐标。
22.数学活动课上,张老师引导同学进行如下探究:将长为的铅笔AB斜靠在垂直于水平桌面AE的直尺FO的边沿上,一端固定在桌面上,图乙是示意图.如图丙所示,将铅笔AB绕端点按顺时针方向旋转,AB与OF交于点,当旋转至水平位置时,铅笔AB的中点与点重合.
(1)设,点到OF的距离.请回答下列问题:
①用含的代数式表示:AD的长是 的长是 ;
②写出关于的函数表达式: ,自变量的取值范围是 .
(2)①列表:根据第(1)题中求出的函数表达式计算并补全表格;
6 5 4 3.5 3 2.5 2 1 0.5 0
0 0.55 1.2 1.58 2.47 3 4.29 5.08
②描点:根据表中的数值,在平面直角坐标系(如图丙所示)中描出①中剩余的两个点;
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
(3)请你结合函数的图象,写出关于该函数的两条性质或结论.
一、单选题
1.下列函数中,y是x的反比例函数的是( )
A.x(y﹣1)=1 B.y=
C.y= D.y=
2.下列图象中是反比例函数y=﹣ 图象的是( )
A. B.
C. D.
3.一次函数y1=kx+b和反比例函数y2= 的图象如图,则使y1>y2的x范围是( )
A.x<﹣2或x>3 B.﹣2<x<0或x>3
C.x<﹣2或0<x<3 D.﹣2<x<3
4.如图,A为反比例函数y=(k>0)图象上一点,AB⊥x轴于点B,若S△AOB=3,则k的值为( )
A.1.5 B.3 C. D.6
5.如图,在平面直角坐标系中,点A在第一象限。AB⊥y轴于点B,函数y= (x>0)的图象与线段AB交于点C,且AB=3BC.若△AOB的面积为12.则k的值为( )
A.4 B.6 C.8 D.12
6.反比例函数y= 的图象上,当x<0时,y随x的增大而增大,则m的取值范围是( )
A.m>-2 B.m<0 C.m<-2 D.m>0
7.如图,直线y=-x与双曲线y= 的图象交于A、B两点,过点A作AC⊥y轴于点C,连接BC,若S△ACB=4,则k的值为( )
A.-4 B.4 C.-8 D.8
8.如图,平行四边形AOBC中,∠AOB=60°,AO=8,AC=15,反比例函数y= (x>0)图象经过点A,与BC交于点D,则 的值为( )
A. B. C. D.
9.古希腊数学家帕普斯利用反比例函数的图象和性质解决了三等分角问题,其方法如下:如图,在直角坐标系中,锐角的边OB在x轴正半轴上,边OA与的图象交于点A,以A为圆心,2OA为半径作圆弧交函数图象于点C,取AC的中点P,则.若,则k的值为( )
A. B. C. D.
10.如图所示,在直角平面坐标系Oxy中,点A、B、C为反比例函数y= (k>0)上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则( )
A.S1=S2+S3 B.S1>S2=S3 C.S3>S2>S1 D.S1S2<S32
二、填空题
11.已知反比例函数y=,当x<0时,y随x的增大而减小,那么k的取值范围是 .
12.已知函数满足下列两个条件:①当 时, 随 的增大而减小;②它的图象经过坐标原点,请写出一个符合上述条件的函数的表达式 .
13.如图,点A在反比例函数y= (x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若 = ,△AOB的面积为6,则k的值为 .
14.如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y= 的一个分支上,过C点的直线y=﹣x+b与双曲线的另一个交点为E,则△EOC的面积为 .
15.如图,菱形的边在轴,点在第一象限,且,将这个菱形向右平移2个单位得到菱形(点和对应).若反比例函数的图象恰好经过点,则的值为 .
三、解答题
16.已知y=y1+y2,y1与x成正比例,y2与x+2成反比例,且当x=﹣1时,y=3;当x=3时,y=7.求x=﹣3时,y的值.
17. 如图,在平面直角坐标系中,为坐标原点,的边垂直于轴,垂足为点,反比例函数的图象经过的中点,交于点,且若点的坐标为.
(1)求反比例函数的表达式.
(2)设点是轴上一动点,若的面积等于,求点的坐标.
18.如图,Rt△ABO的顶点A是双曲线 与直线y= x (k+1)在第二象限的交点,AB⊥x轴于B且S△ABO= 。
(1)求这两个函数的解析式。
(2)求直线与双曲线的两个交点A,C的坐标和△AOC的面积。
19.如图所示,已知一次函数y=kx+b(k≠0)的图象与反比例函数y= 的图象交于A、B两点,且点A的横坐标和B点的纵坐标都是﹣2,求△AOB的面积.
20. 如图,已知反比例数的图象与一次函数的图象相交于点,,过点作轴于点,过点作轴于点,连结.
(1)求反比例函数和一次函数的解析式;
(2)观察图象,直接写出一次函数值大于反比例函数值时自变量的取值范围;
(3)求四边形的面积.
21.如图,△PAB的直角顶点P在第四象限,顶点A、B分别落在反比例函数 图象的两个分支上,且PB⊥x轴于点C,PA⊥y轴于点D,AB分别与x轴,y轴相交于点E、F已知B(1,3)
(1)k= ;
(2)试说明AE=BF;
(3)当四边形ABCD的面积为 时,求点P的坐标。
22.数学活动课上,张老师引导同学进行如下探究:将长为的铅笔AB斜靠在垂直于水平桌面AE的直尺FO的边沿上,一端固定在桌面上,图乙是示意图.如图丙所示,将铅笔AB绕端点按顺时针方向旋转,AB与OF交于点,当旋转至水平位置时,铅笔AB的中点与点重合.
(1)设,点到OF的距离.请回答下列问题:
①用含的代数式表示:AD的长是 的长是 ;
②写出关于的函数表达式: ,自变量的取值范围是 .
(2)①列表:根据第(1)题中求出的函数表达式计算并补全表格;
6 5 4 3.5 3 2.5 2 1 0.5 0
0 0.55 1.2 1.58 2.47 3 4.29 5.08
②描点:根据表中的数值,在平面直角坐标系(如图丙所示)中描出①中剩余的两个点;
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
(3)请你结合函数的图象,写出关于该函数的两条性质或结论.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
