11.2三角形全等的判定(ASA、AAS)(广东省中山市)
文档属性
| 名称 | 11.2三角形全等的判定(ASA、AAS)(广东省中山市) |  | |
| 格式 | rar | ||
| 文件大小 | 238.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-12 13:46:00 | ||
图片预览




文档简介
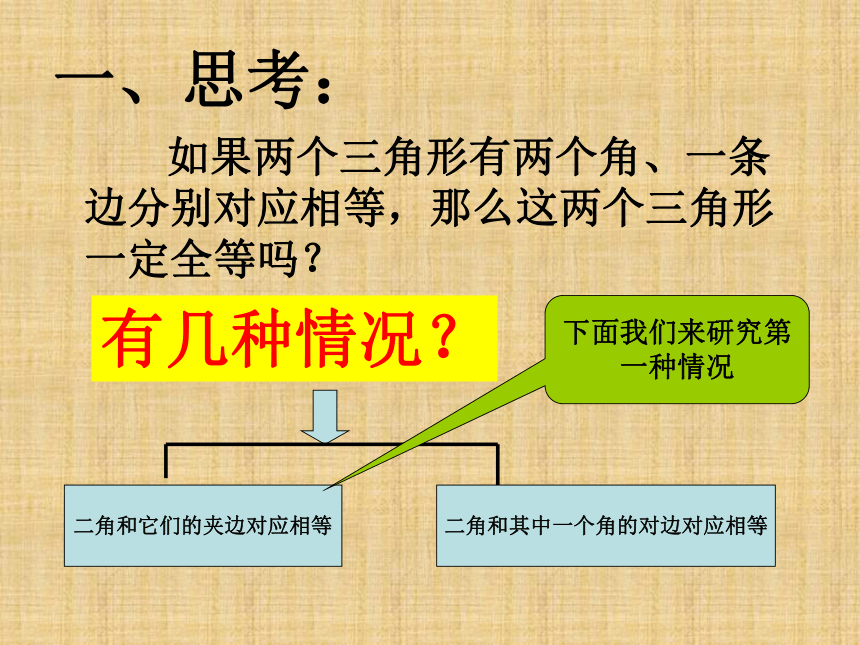
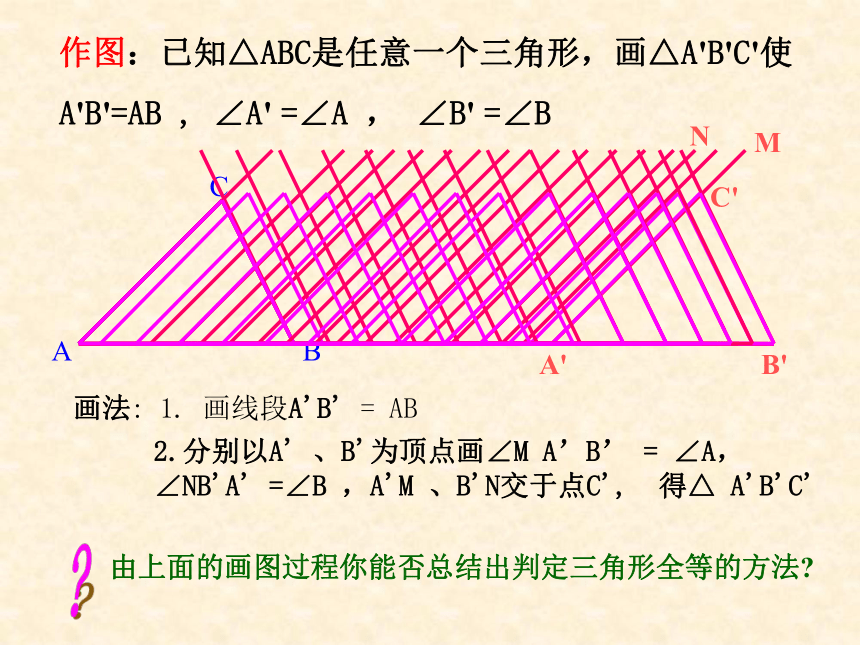
课件16张PPT。11.2 三角形全等的判定(ASA/AAS)分2课时完成一、思考: 如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形一定全等吗?有几种情况?二角和它们的夹边对应相等二角和其中一个角的对边对应相等下面我们来研究第一种情况作图:已知△ABC是任意一个三角形,画△A'B'C'使
A'B'=AB , ∠A' =∠A , ∠B' =∠B画法: 1. 画线段A'B' = AB 2.分别以A' 、B'为顶点画∠M A’B’ = ∠A,
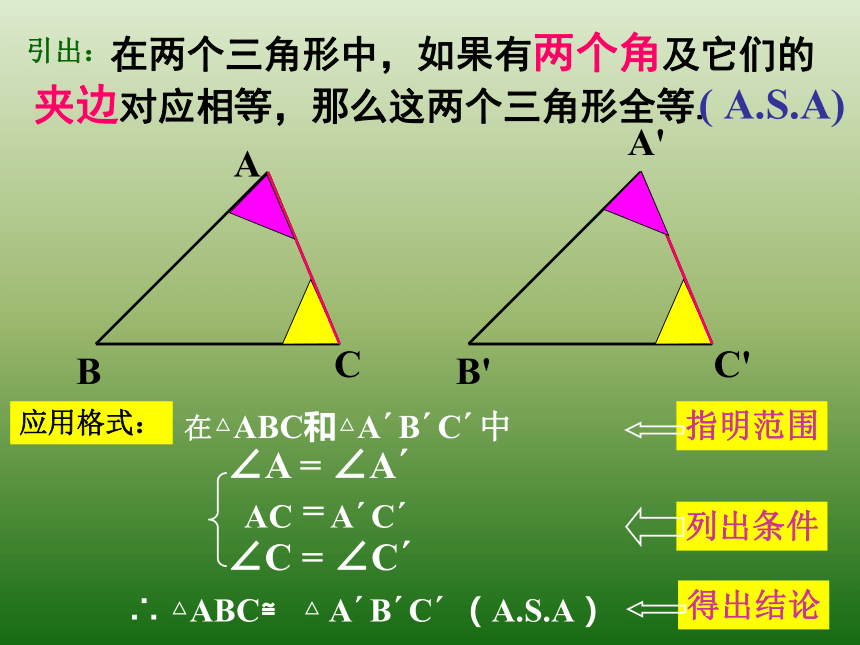
∠NB'A' =∠B ,A'M 、B'N交于点C', 得△ A'B'C'由上面的画图过程你能否总结出判定三角形全等的方法??C' 在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等. ( A.S.A) ∴ △ABC≌ △ A′B′C′ (A.S.A)∠A = ∠A′
=
∠C = ∠C′在△ABC和△A′B′C′中ACA′C′引出:应用格式:1、如图,已知∠ABC=∠DCB,∠ACB= ∠DBC,求证:△ABC≌△DCB.证明:二、应用:DCB
2、已知:点D在AB上,点E在AC上,BE和CD相交于
点O,AB=AC, ∠B=∠C
求证:AD=AEABEO证明: 在△ABE 和△ACD中
∵ ∠A =∠A (公共角)
AB = AC ( 已知 )
∠B =∠C ( 已知 )
∴△ABE≌△ACD( A.S.A)一展身手∴AD=AE( 全等三角形的对应边相等)三、巩固练习:课本13页练习:第1题
15页:第5题四、自我检测:如图,∠1=∠2,∠A=∠D,AB=CD,
求证:△ACE≌△DBFAE=DFABCA’B’C’五、思考: 如图,在△ABC与△A’B’C’中,已知∠A=∠A’,∠B=∠B’,AC=A’C’,△ABC与△A’B’C’全等吗?为什么? 在两个三角形中,如果有两个角和其中一个角的对边对应相等,那么这两个三角形全等.ABCDEF(A.A.S)∴ △ABC≌ △DEF(A.A.S)∠A = ∠D
∠B = ∠E
=
BCEF在△ABC和△DEF中引出:应用格式:在△AOC和△DOB中,
∵ ∠A=∠D(已知)
∠1=∠2(对顶角相等)
CO=BO(已知)
∴△AOC≌△DOB( A. A. S)如图,已知AB与CD相交于O,∠A=∠D,CO=BO,求证:△AOC≌△DOBD证明:六、学以致用ACBO12求证:AC=BD
,你会吗?试比较A.S.A与A.A.S两个判定之 间的区别与联系。思考1:A.S.A与A.A.S都要求有两个角一条对应边相等。A.S.A是两角一夹边而A.A.S是两角一对边。联系:区别: 一般在图形中隐含的条件 有哪些 ?思考2:公共边; 对顶角等。 公共角; 七.小结三角形全等判定方法2:在三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A)。1234三角形全等判定方法3:在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等。(简记为A.A.S)。 三角形全等判定的两个方法A.S.A与A.A.S的区别和联系。 5如何在图形中找出隐含的条件。如公共角、公共边、对顶角等。 注意书写格式,(1)要写出在哪两个三角形中;(2)要按角、边、角或角、角、边的顺序摆出三个条件,(3)写出结论。(书写时,要注意字母的对应关系。) 思考还有没有其它证明三角形全等的方法?八、作业:课本第15—16页:第6、11题九、教学后记:
A'B'=AB , ∠A' =∠A , ∠B' =∠B画法: 1. 画线段A'B' = AB 2.分别以A' 、B'为顶点画∠M A’B’ = ∠A,
∠NB'A' =∠B ,A'M 、B'N交于点C', 得△ A'B'C'由上面的画图过程你能否总结出判定三角形全等的方法??C' 在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等. ( A.S.A) ∴ △ABC≌ △ A′B′C′ (A.S.A)∠A = ∠A′
=
∠C = ∠C′在△ABC和△A′B′C′中ACA′C′引出:应用格式:1、如图,已知∠ABC=∠DCB,∠ACB= ∠DBC,求证:△ABC≌△DCB.证明:二、应用:DCB
2、已知:点D在AB上,点E在AC上,BE和CD相交于
点O,AB=AC, ∠B=∠C
求证:AD=AEABEO证明: 在△ABE 和△ACD中
∵ ∠A =∠A (公共角)
AB = AC ( 已知 )
∠B =∠C ( 已知 )
∴△ABE≌△ACD( A.S.A)一展身手∴AD=AE( 全等三角形的对应边相等)三、巩固练习:课本13页练习:第1题
15页:第5题四、自我检测:如图,∠1=∠2,∠A=∠D,AB=CD,
求证:△ACE≌△DBFAE=DFABCA’B’C’五、思考: 如图,在△ABC与△A’B’C’中,已知∠A=∠A’,∠B=∠B’,AC=A’C’,△ABC与△A’B’C’全等吗?为什么? 在两个三角形中,如果有两个角和其中一个角的对边对应相等,那么这两个三角形全等.ABCDEF(A.A.S)∴ △ABC≌ △DEF(A.A.S)∠A = ∠D
∠B = ∠E
=
BCEF在△ABC和△DEF中引出:应用格式:在△AOC和△DOB中,
∵ ∠A=∠D(已知)
∠1=∠2(对顶角相等)
CO=BO(已知)
∴△AOC≌△DOB( A. A. S)如图,已知AB与CD相交于O,∠A=∠D,CO=BO,求证:△AOC≌△DOBD证明:六、学以致用ACBO12求证:AC=BD
,你会吗?试比较A.S.A与A.A.S两个判定之 间的区别与联系。思考1:A.S.A与A.A.S都要求有两个角一条对应边相等。A.S.A是两角一夹边而A.A.S是两角一对边。联系:区别: 一般在图形中隐含的条件 有哪些 ?思考2:公共边; 对顶角等。 公共角; 七.小结三角形全等判定方法2:在三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A)。1234三角形全等判定方法3:在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等。(简记为A.A.S)。 三角形全等判定的两个方法A.S.A与A.A.S的区别和联系。 5如何在图形中找出隐含的条件。如公共角、公共边、对顶角等。 注意书写格式,(1)要写出在哪两个三角形中;(2)要按角、边、角或角、角、边的顺序摆出三个条件,(3)写出结论。(书写时,要注意字母的对应关系。) 思考还有没有其它证明三角形全等的方法?八、作业:课本第15—16页:第6、11题九、教学后记:
