11.3角平分线的性质(1)
文档属性
| 名称 | 11.3角平分线的性质(1) |  | |
| 格式 | rar | ||
| 文件大小 | 257.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-13 20:19:00 | ||
图片预览

文档简介
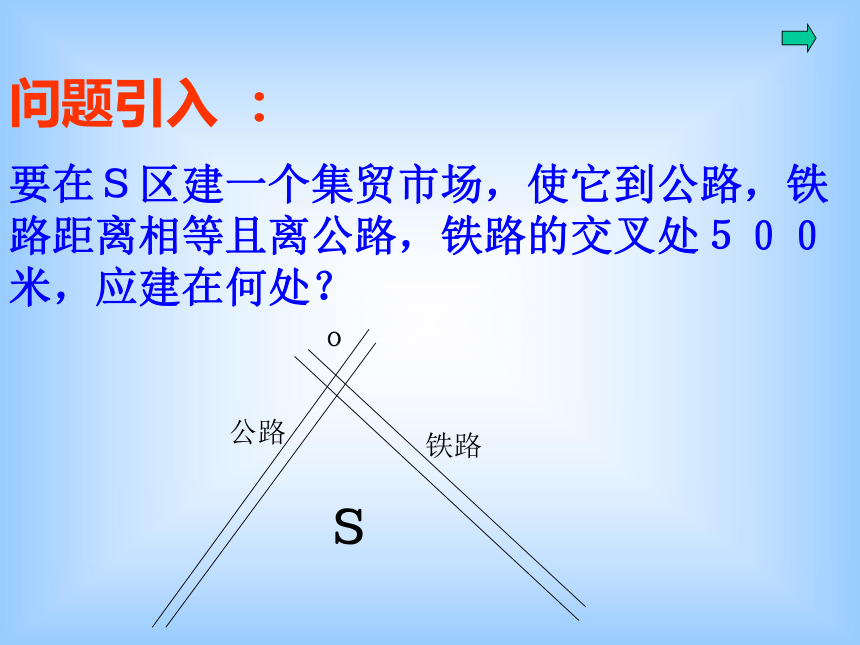
课件11张PPT。13.3角平分线的性质(1)问题引入 :
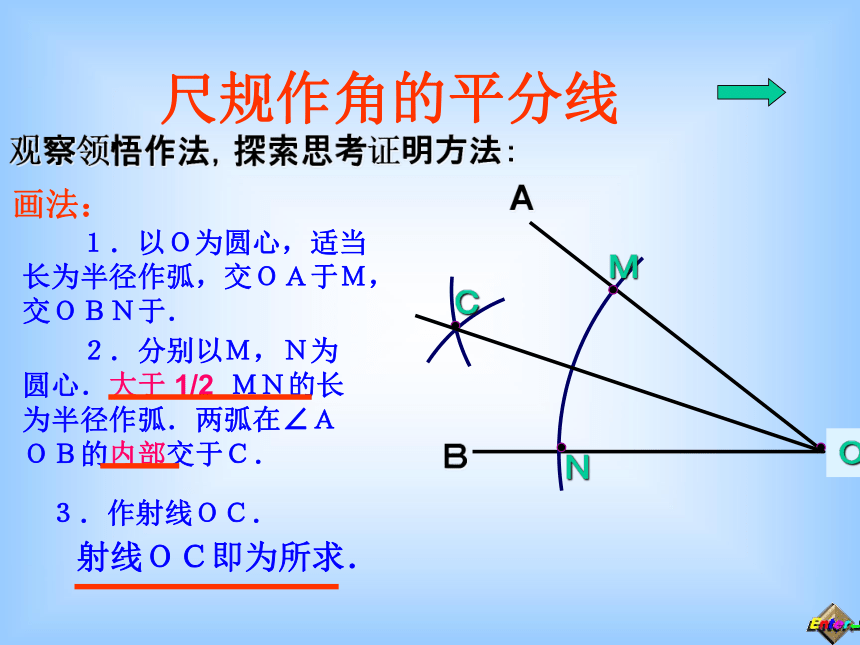
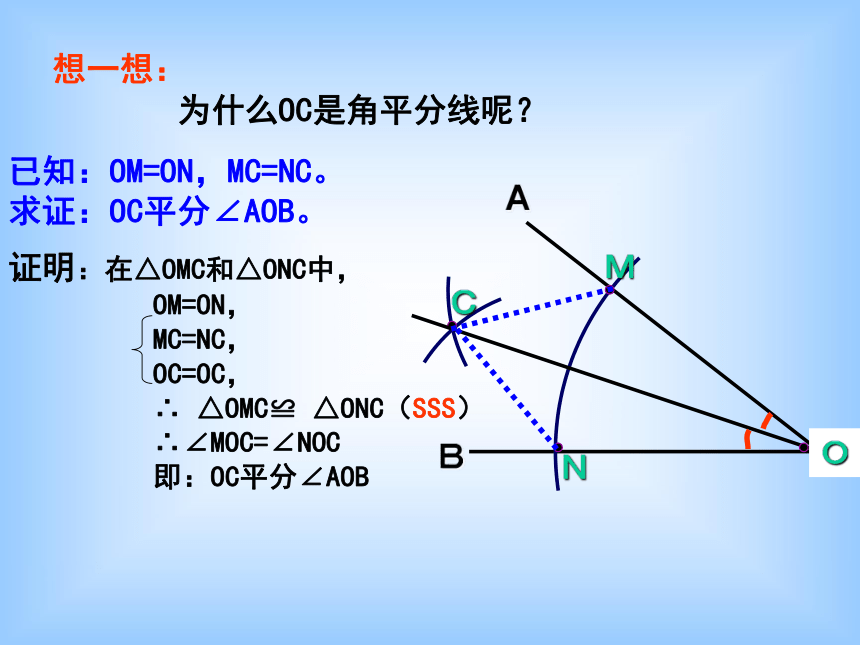
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?SO公路铁路尺规作角的平分线观察领悟作法,探索思考证明方法:AB画法: 1.以O为圆心,适当长为半径作弧,交OA于M,交OBN于. 2.分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.3.作射线OC.射线OC即为所求.AB为什么OC是角平分线呢? O想一想:已知:OM=ON,MC=NC。
求证:OC平分∠AOB。证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
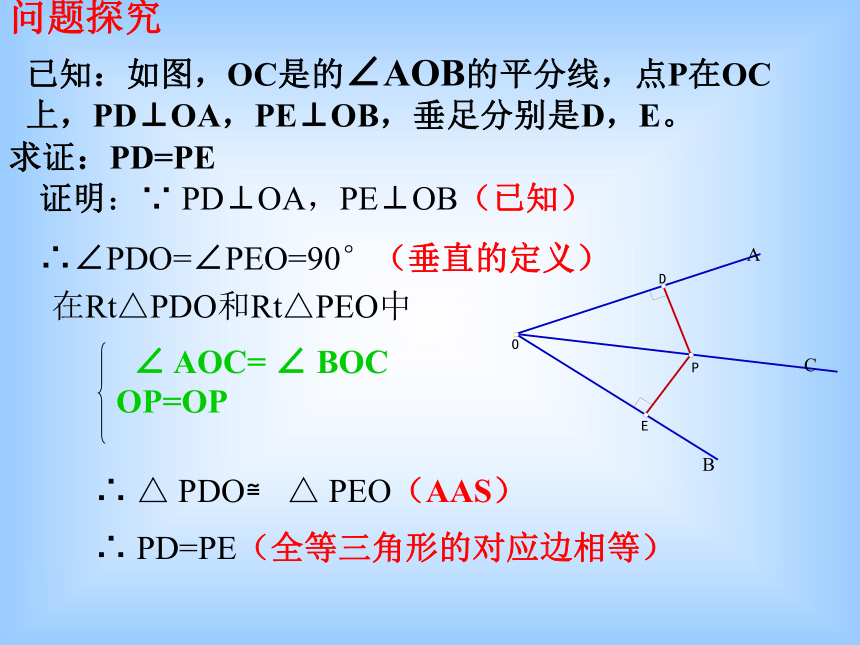
即:OC平分∠AOB已知:如图,OC是的∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。求证:PD=PE证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90°(垂直的定义)在Rt△PDO和Rt△PEO中∴ PD=PE(全等三角形的对应边相等) ∠ AOC= ∠ BOC OP=OP∴ △ PDO≌ △ PEO(AAS)问题探究∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( ) 角的平分线上的点到角的两边的距离相等。
角平分线的性质:角平分线上的点到角的两边的距离相等 符号表示,OABED思考:如图所示OC是∠AOB 的平分线,P 是OC上任意一点,问PE=PD?为 什么?CPPD,PE没有垂直OA,OB,它们不是角平分线上任一点这个角两边的距离,所以不一定相等 △ABC中, ∠C=900,AD平分∠ CAB,且 BC=8,BD=5,求点D到AB的距离是多少?ABCDE知识应用问题引入 :
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)SO公路铁路,说一说 请同学们说一说这节课你有哪些收获和体会。
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?SO公路铁路尺规作角的平分线观察领悟作法,探索思考证明方法:AB画法: 1.以O为圆心,适当长为半径作弧,交OA于M,交OBN于. 2.分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.3.作射线OC.射线OC即为所求.AB为什么OC是角平分线呢? O想一想:已知:OM=ON,MC=NC。
求证:OC平分∠AOB。证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB已知:如图,OC是的∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。求证:PD=PE证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90°(垂直的定义)在Rt△PDO和Rt△PEO中∴ PD=PE(全等三角形的对应边相等) ∠ AOC= ∠ BOC OP=OP∴ △ PDO≌ △ PEO(AAS)问题探究∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( ) 角的平分线上的点到角的两边的距离相等。
角平分线的性质:角平分线上的点到角的两边的距离相等 符号表示,OABED思考:如图所示OC是∠AOB 的平分线,P 是OC上任意一点,问PE=PD?为 什么?CPPD,PE没有垂直OA,OB,它们不是角平分线上任一点这个角两边的距离,所以不一定相等 △ABC中, ∠C=900,AD平分∠ CAB,且 BC=8,BD=5,求点D到AB的距离是多少?ABCDE知识应用问题引入 :
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)SO公路铁路,说一说 请同学们说一说这节课你有哪些收获和体会。
